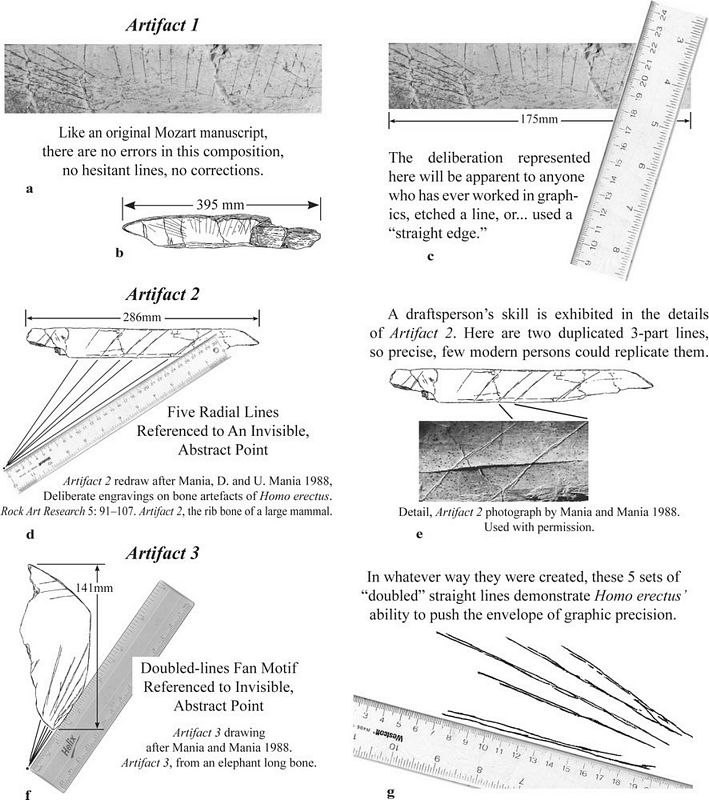The Graphics of Bilzingsleben - full text html with figures

“You show pretty unambiguously that those engravings [which are 400,000 years old] are in no sense archaic.”

- International authority in the history of art and philosophy, 2006

“Absolutely outstanding and stunning. You have single-handedly demonstrated that the cognition and intellect of these hominins may have been of an order entirely unexpected by all of us ... breathtaking ... a landmark contribution.”

- Robert G. Bednarik, session chair, Pleistocene Palaeoart of the World, 2006

“Archaeologists will try every trick in the book to reject your interpretation of the engravings. It is entirely unacceptable to them that they were completely wrong about the cognitive abilities of these people… you do have science on your side... a proposition that is utterly falsifiable. Everyone can repeat your experiment, and the engravings are fixed in time and space. If your calculations are correct… the archaeologists will be stumped.”

- Renowned international authority, 2007, approximately 5 months after Graphics & Phi were presented

Click this link for details on why and how The Graphics of Bilzingsleben was censored for five years beginning within one week of its presentation.

“I have consulted various people… there is complete agreement that your innovative evaluation of the Bilzingsleben engravings is utterly brilliant.”

- Collective conclusion of many scholars with backgrounds in linguistics, neuroscience, psychology, archaeology, and engineering, 2007. Scholars had copy of 8-page thumbnails handout with all 112 slides.

“Brilliant insights of a kind more conventional researchers would not dream of.”

- Neuroscience author attending The Graphics of Bilzingsleben in 2006, quote arrived early 2007

“Brilliant insights that scientists are often barred from, through the nature of their method.”

- Quote of the same neuroscience author as above arriving a mere two days later, early 2007

“I find the data you presented in Lisbon of outstanding importance and believe that they must be published prominently.”

- Renowned international authority, engineer, early 2007

“[Your Bilzingsleben work] goes way beyond…theory of phosphene/entoptic/doodles and way beyond any prior interpretation of the ‘savage mind’ of Homo erectus.”

- International authority on Paleolithic art 17 months after presentation

“Totally brilliant analysis.”

- Same authority as prior quote after looking over the materials more thoroughly

“This is very exciting! I think the only thing you might have to fight is the erectus-heidelbergensis issue; but in comparison to what you have demonstrated here, that is not important at all.”

- Physical anthropology expert and author attending The Graphics of Bilzingsleben, paraphrase of direct comment.

“An absolutely thrilling presentation.”

- Antiquity author attending The Graphics of Bilzingsleben presentation. This was the first response immediately after the presentation and encapsulated the mood of the entire audience.

To cite this paper: Feliks, J. 2011. The Graphics of Bilzingsleben: Sophistication and subtlety in the mind of Homo erectus. In Oosterbeek, L. and C. Fidalgo (eds), Proceedings of the XV UISPP World Congress (Lisbon, 2006), British Archaeological Reports International Series 2224, Oxford, pp. 71-91.

Return to English main page

THE GRAPHICS OF BILZINGSLEBEN:
SOPHISTICATION AND SUBTLETY IN THE MIND OF
HOMO ERECTUS*

John Feliks
U.S.A. E-mail: feliks (at) umich.edu

*This paper is the first half of a two-part program which the author presented at the XVth UISPP Congress, September 7, 2006. The second half was Program #C80-06, ‘Phi in the Acheulian: Lower Palaeolithic intuition and the natural origins of analogy.’

Abstract: In 1988, Dietrich and Ursula Mania published images of unmistakably deliberate engravings on bone artifacts dated between 320,000-412,000 years BP, found near the village of Bilzingsleben in central Germany. Contrary to traditional notions of early peoples, Mania and Manias’ preliminary interpretations suggested that these markings implied the existence of advanced human traits, which included abstract thinking, language, and a “concept of the world.” In this presentation, I will demonstrate that the Bilzingsleben markings go well beyond these already stunning assertions, and document a very large number of graphic innovations and highly advanced intellectual traits in Homo erectus, innovations and traits that have long been regarded the exclusive domain of Homo sapiens. In fact, the artifacts contain so much information that, collectively, they constitute nothing less than a detailed and expansive map directly into the extraordinary mind of this early ancestor. I will demonstrate that the markings reflect graphic skills far more advanced than those of the average modern Homo sapiens. A new list of qualities, abilities, and innovations which must now be credited to Homo erectus, and which are directly indicated by the markings includes: abstract and numeric thinking; rhythmic thinking; ability to duplicate not only complex, but also, subtle motifs; iconic and abstract representation; exactly duplicated subtle angles; exactly duplicated measured lines; innovative artistic variation of motifs including compound construction, doubling, diminution, and augmentation; understanding of radial and fractal symmetries; impeccably referenced multiple adjacent angles; and absolute graphic precision by high standard and, practically, without error. Each of these will be demonstrated visually. Hence, the following advanced cognitive qualities may be quite easily assumed for the species Homo erectus by way of geometric analogy: interrelationship sensitivity and complex organizational skill; language; use of metaphor and hidden meaning; philosophy; mysticism or other “spiritual” perspectives; and a general ability to discern, appreciate, and create the most subtle nuance within any area of intellectual endeavor.

Keywords: Cognitive Archaeology – Bilzingsleben – Bach – Linguistics – Cartography

INTRODUCTION

It is a long-standing axiom of modern science that human intelligence evolved slowly over time and that our own species, Homo sapiens, is the obvious pinnacle of an evolutionary sequence. In this paper, however, I will provide unambiguous geometric evidence that the above-mentioned axiom may be wrong on both counts. First, I propose that the engravings from Bilzingsleben, an Acheulian age Homo erectus site in central Germany (dated 320,000-412,000 years before the present) offer more than enough evidence to conclude that there has been no increase in the innate intelligence of Homo sapiens individuals over Homo erectus individuals despite a 200,000-300,000-year time span in which Homo sapiens could have accomplished this; and second, I propose that the real per capita pinnacle of human culture in degree, and the crucial point in time at which the modern intellectual condition was attained are each within the purview of Homo erectus. In effect, what I am proposing is that all individuals of the genus Homo use intelligence either to the degree they choose or the degree to which they are constitutionally capable; however, the intelligence of the genus as a whole never changes.

It is almost unanimously accepted in the scientific community that what is called “cognitive evolution” (a gradual increase in human intelligence) is observable in the archaeological record not only over millions of years time but also over smaller periods, even tens of thousands of years time. This is simply not the case, for unlike in the easy-to-confirm sciences (e.g., biology, genetics, physics, etc.) which are characterized by a never-ending supply of material or subjects for real-time observation or testing, the study of early human cognition is characterized by an incredibly small amount of evidence with which to work and no real-time access whatsoever. This clearly makes the task of understanding early human cognition far more difficult a challenge than virtually any other science. However, when one looks at the evidence that is available from an interdisciplinary point of view it is seen to be quite far from suggesting a cognitive evolution of any kind. Although, it is still possible to move the continuously changing sliding scale of modern human cognition attainment farther and farther back in time, the evidence as it now stands does not support Darwin’s 1859 proclamation that each mental capability will be shown to have been necessarily acquired by “gradation” (Charles Darwin, The Origin of Species, 1859: 488).

When studying the cognition of early peoples, dedication to preconceived artificial notions such as cognitive evolution can be powerfully limiting. For example, the engravings from Bilzingsleben have been available for 20 years now (since Mania and Mania 1988); but since they were always considered in the predetermined context of “Homo erectus the ape-man,” it was highly unlikely that they would ever be seen as having been engraved with a straight edge despite the exceptional straightness of the

Page 71

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 72

lines comprising them. If anything should humble modern Homo sapiens and cause us to question our presumed position as the pinnacle of evolution, it is the very real possibility that these straight edge-engraved artifacts, which are demonstrably profound, are neither a fluke nor even the work of genius but rather are reflective of Homo erectus intelligence in general. Based on the developed level of subtlety these artifacts exhibit, it is likely that they were influenced by traditions or ideas taught or passed down already for many generations. And certainly, if we apply modern psychological or sociological principles that all individuals are a product of their community in one way or another, then at the very least, we must see the engraved artifacts of Bilzingsleben as reflective of all Homo erectus people living at that particular time and in that particular region. It is only one step further, as explained in Part V, to compare physical and cultural similarities between the Homo erectus people of Bilzingsleben and their contemporaries living in other parts of the world in making these principles applicable to the species as a whole worldwide. In all, the real evidence is quite contrary to the preconceived notion of cognitive evolution that has given us a view of these ancestors as ape-men rather than as the remarkable innovators they actually were.

It is my hope in this paper to demonstrate that the people of Bilzingsleben, and other Lower Palaeolithic peoples dating as far back as 2 million years, were highly advanced intellectually, including mathematically and philosophically, long before we stepped into the picture, and that this is provable by way of basic geometry (Euclidean and fractal), trigonometry, representation, and linguistics. From this perspective, I suggest that the question of whether or not these peoples had language should no longer be asked. In fact, the buffer-zone notion that early peoples must have had some sort of “rudimentary” language should also be withdrawn because the evidence from Bilzingsleben alone unambiguously indicates cognition as highly developed as anything present in today’s modern world.

PRESENTATION OF MATERIAL

The thesis will proceed entirely by way of its figures which are basically consolidations of the original slides and thumbnails handout presented at the Congress. The entire program was conceived as only a visual thesis rather than thesis paper. The idea was essentially to allow the Bilzingsleben engravings to speak for themselves visually by merely drawing attention to their geometric qualities. (The studies offered here represent only a portion of those that were produced for the program.) Since the figures are for the most part self-contained, from this point onward, one may go directly to the figures (Figs. 7.1-7.16, in any order) or read the following explanatory sections.

Overview: PARTS I, II, & III (STRAIGHT EDGE THEORY, THE EARLIEST MOTIF DUPLICATED ON TWO SEPARATE ARTIFACTS, and 350,000 YEARS BEFORE BACH) involve methods of approaching Lower Palaeolithic language. PART IV (TOWARD THE REALM OF IDEAS) relates to geometric means of accessing Lower Palaeolithic mathematics, philosophy and abstract thinking. The purpose of PART V (WHO WERE THE PEOPLE OF BILZINGSLEBEN?) is to place all of this extremely abstract material into the more accessible context of real people who were not unlike us although this contrasts the image promoted by popular science which discusses early peoples as being lesser-developed than ourselves. Since the human remains from Bilzingsleben are essentially the same as those of their 400,000 year-old contemporaries in Africa, China, and Indonesia (a fact that tends to be avoided in scientific literature), the cultural evidence of Bilzingsleben and elsewhere also supports a consolidated image of our ancestors worldwide as one interrelated group. Finally, PART VI (TWO SKETCHES FROM BILZINGSLEBEN) would certainly seem absurd to readers of modern science were it presented without first reassessing entirely the intelligence of Homo erectus people toward whom I am hoping, by this point, readers will have no difficulty whatsoever considering their capability for cartography.

INFLUENCES AND POSITION IN A LARGER SYSTEM

The theoretical aspects of this paper were inspired by and owe a great debt to the work of Mania and Mania, Bednarik, Gowlett, Mikiten, Dissanayake, Chomsky, Sacks, White, Capra, and others. And while its use in archaeology may seem at first unwarranted, many ideas regarding the Bilzingsleben graphics were drawn from knowledge regarding the musical style of J.S. Bach, especially Bach’s use of extra-musical effects linked with his little-known mystical/philosophic interests (Feliks 1992, 1993, 1994). Indebtedness to Plato will also be readily apparent throughout.

The 3D map section requires additional explanation, as its influences, apart from the fractal aspects, were quite different from those of the other sections. They included studies of Sumerian, Minoan, Medieval and Renaissance maps (primarily 3D picture maps), and the geometries of megalithic sites. The earliest maps are sometimes referred to in the literature as “attempts” at cartography. However, what I am proposing as the Bilzingsleben map, at 320,000-412,000 years old, is far from timid. In fact, it exudes a seasoned confidence and style, with a quality and accuracy uncommon even in many Discovery Age maps. It certainly equals the precision and style of the famed Catal Huyuk town plan of 6200 B.C. (created about 3000 years before the first cuneiform script). The map section contains only a small portion of the author’s systematic work on the layout of Bilzingsleben especially as it relates to Bilzingsleben Artifact 6.

It is through conclusions reached by a 15-year study and confidence in the work of the above-mentioned researchers, as well as such as Oakley and Marshack, that

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 73

I decided to approach the matter of early human cognition from the top down rather than the traditional bottom up. I worked from the principle that once any single profoundly advanced capability is proven, no matter how unlikely it may seem at first (e.g., use of a straight edge), that we can safely assume every other modern cognitive ability to have also been present. To my surprise, this approach required no downward movement of any kind. This is part of what led to a system of study based in large part on fractals. It is a system which I regard as fully capable of translating the “core ideas” of Lower and Middle Palaeolithic peoples. In this fractal system, individual facts work as complete concepts rather than in the traditional way like mere letters of an alphabet. This is a very economical use of facts and enables access to complex Palaeolithic ideas which would traditionally be deemed inaccessible without text or representational images.

DISCLAIMERS AND NOMENCLATURE

Except for in the Bach section as noted below, all geometric studies are of the utmost accuracy and exactly as stated. The angles—measured with the protractor seen in Figures 7.5 and 7.9—are also exactly as stated and refer to the superimposed lines. Any deviations, e.g., the rounding of angles, are usually within one-half a degree. In all cases, the tolerances applied are clearly visible. It should be noted, however, that Mania and Mania’s original drawings were not made with such meticulous studies in mind, so qualities of the actual artifacts may vary slightly.

Minor adjustments were made in the Bach section involving the spacing of vertical lines. These were tempered so as to make for easier viewing of the interpretations offered.

It is important to emphasize that the topic of this paper is early human cognition and not biological evolution. However, the more completely I studied the Bilzingsleben engravings the more I realized that their cognitive implications did not at all align with the standard picture of Homo erectus long-promoted by the scientific community. Since it became increasingly clear that the inhabitants of Bilzingsleben were not “half-way-there” intellectually, it stood to reason that they may also not be intellectually different from other Lower Palaeolithic peoples living at the same time. Therefore, I will generalize by referring to all Lower Palaeolithic peoples as a single group, namely Homo erectus, rather than specify whether or not certain researchers regard local populations as erectus, ergaster, heidelbergensis, etc. I will explain this position further in Parts I and V. To be clear, this paper is about Lower Palaeolithic cognition regardless of the species involved.

Finally, I wish to say that my background is in the arts, not mathematics, and that my approach to mathematics is by choice artistic and poetic. And even though I am using mathematics as the primary structure of this paper, it is not my intention to create an impression of early peoples as being any more focused on mathematics as anything else. Rather, I am attempting to prove by way of testable mathematical and linguistic capabilities that early peoples were just as diverse as we are today and with as many different abilities and interests.

PART I
STRAIGHT EDGE THEORY: BEGINNING ACCESS TO A
LOWER PALAEOLITHIC LANGUAGE (Figures 7.1, 7.2, 7.3, and 7.4)

The groundwork for straight edge theory was laid out in a prior publication (Feliks 2006). The visual data offered in the original paper and this new paper is straightforward, confirmable by direct observation, and testable on the page by anyone. It clearly indicates that the engravers of the Bilzingsleben artifacts used a straight edge to facilitate creation of the many subtle radial patterns and parallels featuring perfectly straight lines. The proposal is demonstrated in this paper by direct comparison of the Bilzingsleben engraved motifs with modern standard-increment rulers, the proposed Bilzingsleben rib-bone “ratio ruler,” and by superimpositions of duplicated radial motifs.

The idea that Homo erectus could have used a straight edge had never been considered in science for one simple reason: the necessity of retaining in the evolutionary paradigm an assumed ‘cognitive half-way-there zone’ between early ape-like creatures such as Ardipithecus and modern Homo sapiens. Accepting this assumption as a central axiom, the scientific community in general has long been pre-convinced that Homo erectus was unable even to speak let alone create engravings of a quality level suggesting the work of modern draftspersons or technical designers. Prior to publication of Mania and Mania’s 1988 paper, Deliberate engravings on bone artifacts of Homo erectus, it was considered by most in archaeology that markings on Lower and Middle Palaeolithic bone artifacts were likely a by-product of nothing more intentional than scraping the bones for meat. Not surprisingly, and due to universal acceptance of the paradigm, publication of the images did not result in an immediate reversal of opinion, either. In fact, so engrained has the “ape-man” perspective of Homo erectus been that the idea has budged very little even two decades after Mania and Mania published the engravings. The most profound effect seems to be that of a debated name change for the Bilzingsleben hominids from Homo erectus to Homo heidelbergensis. H. heidelbergensis serves as a mere buffer-zone species between H. erectus and H. sapiens and is regarded arbitrary by some researchers. Still, even if the name heidelbergensis were adopted, the switch would be a moot choice of association as the straight edge studies point to a level of technology not even attributed to Homo sapiens until 350,000 years later.

Significance of Straight edge theory: Employing a straight edge to make either single straight lines or radial

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 74

Figure 1. Straight edge theory: Artifacts 1–3. Note: The Artifacts 1–6 numbering system is from Mania and Mania 2005. Rulers were superimposed by J. Feliks. (a & c) Detail, Artifact 1 engravings cropped from photograph by R. Bednarik 1997. Used with permission. Artifact 1 is the tibia bone of a straight-tusked elephant. (b) Artifact 1 after Mania and Mania 1988. (d) Artifact 2, the rib bone of a large mammal, after Mania and Mania 1988. (e) Detail, Artifact 2 engravings showing duplicated 3-part compound motifs, cropped from photograph by Mania and Mania 1988. Used with permission. (f) Artifact 3 after Mania and Mania 1988. (g) Close-up, double-engraved lines of Artifact 3.

motifs is unmistakably clear evidence not only for language but for highly-evolved language and mathematical abilities. The link is the concept of analogy at two levels. At the basic level, the straight edge in and of itself is a profoundly simple analogical invention easily associated with language because a line engraved with the aid of a straight edge is directly symbolic of the straight edge

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 75

Figure 2. Fig. 7.2. Straight edge theory, Artifacts 3–6. (a) Detail, Artifact 3, highlighting an unambiguously straight engraved angle tapered at less than 2° and comparable to modern standards of quality. Photograph by Mania and Mania 1988. Used with permission. (b) Artifact 4, a flat piece of bone, after Mania and Mania 1988. (c) Detail, Artifact 4 photograph, Mania and Mania 1988. (d) Extreme close-up, Artifact 4 photograph. Mania and Mania 1988. Used with permission. (e) Artifact 5. Bednarik 1995. Certainly, straight lines engraved on a slab of stone cannot be explained away as survival behavior. Used with permission. (f) Artifact 6. This work represents either simple musings by someone fascinated with straight lines and trig angles or a highly purposeful arrangement. (g) Engravings from Artifact 6 isolated—highlighting presence of the special trig angles 30, 45, 60, 90; parallels, diagonals, perpendiculars, and planes—all within ±3° deviation. Apart from a few slight curves, the draftsmanship consists entirely of straight lines likely drawn with an edge. “Non-obvious parallel etchings” were bolded and color-coded.

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 76

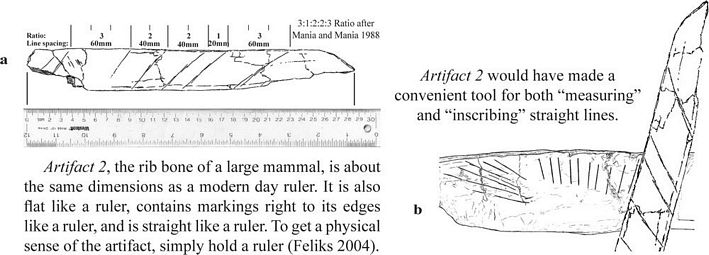Figure 3. Proposed early straight edge. (a) Artifact 2 compared with a modern ruler. (b) Proposed early straight edge in use. (Artifact 2 after Mania and Mania 1988, Artifact 1 drawing after photograph by R. Bednarik 1997.).

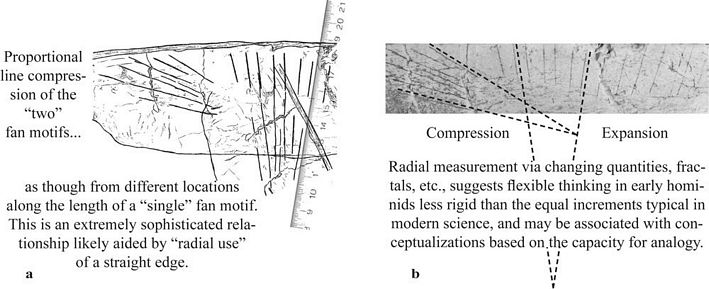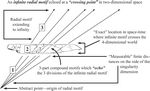
Figure 4. Straight edge theory and the “Realm of Ideas.” (a) Proportional line compression of “two” fan motifs as though from different locations along the length of a “single” fan motif. Referring to Plato’s “realm of ideas” or “theory of forms,” the two motifs in Artifact 1 suggest an awareness of the fan shape or radial image in a way that transcends simple observation of the physical world or as writers such as Morris (1962) or Gowlett (1984) might refer to as a “mental template.” (b) Compression-expansion and one means by which radial measurement (or ratio measurement as in the Part 2 paper) can be a geometric equivalent of analogy (Artifact 1 drawing after photograph by Bednarik 1997, Detail Artifact 1 cropped from photograph by R. Bednarik 1997. Used with permission.).

itself, being a “representation” of the edge. This clearly indicates that Homo erectus understood the association between a physical object and a graphic representation of a particular quality of that object, i.e. its straightness. It is analogous in language to a spoken word or graphic symbol being used to represent an object, a person, or an idea.

On a more complex and genuinely unlimited level both philosophically and mathematically, a central thesis of this paper is that multiple straight edge-engraved lines forming “radial motifs” is a confirmation that the people of Bilzingsleben fully understood the concept of analogy or that one idea can be compared with another. Any analogy based on radial symmetry can be instantly applied to philosophical or mathematical ideas; e.g., Fig. 7.4a & b, “The Realm of Ideas,” where one portion of a radial motif can be readily compared with another portion because angles remain the same at any magnification or distance; Fig. 7.9, “Fractal Angle Symmetry,” where duplicated angles may branch off of base angles; and Figs. 7.11–7.14, where small motifs can be used to imply association with larger or even infinite motifs. Regardless of how unlikely these claims may seem under the old paradigm view of Homo erectus, use of a straight edge to create radial motifs demonstrates that Homo erectus

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 77

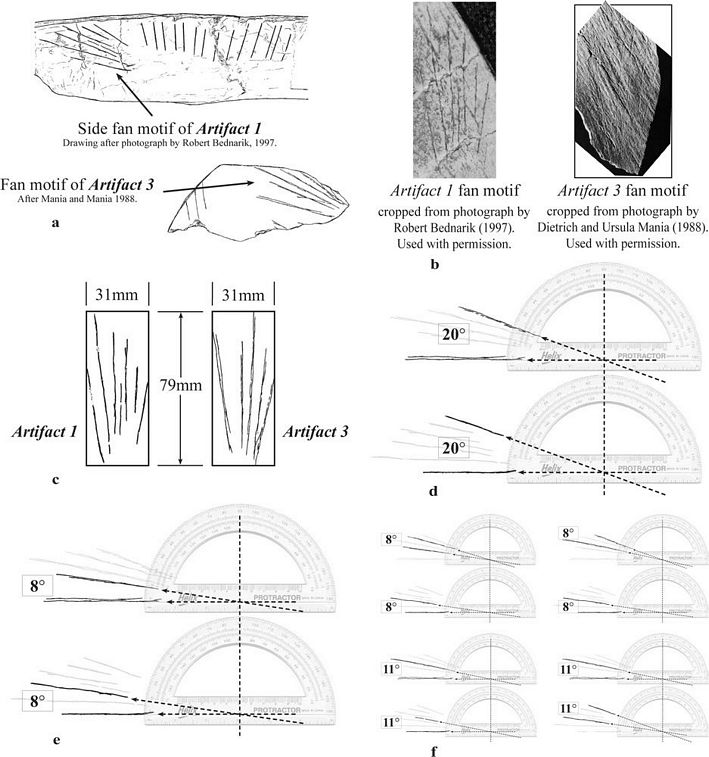Figure 5.The earliest motif duplicated on two separate artifacts. Part 1. (a) The motifs in context with other syntactic variables. (b) Photographs. (c) Observation 1: The motifs are the same size. (d) Observation 2: The motifs share “identical” outer angles. (e) Observation 3: The motifs share identical “inner” angles. (f) Observation 4: The motifs share many other identical angles. Beyond the angles detailed in this paper, there are at least 5 more near identical angles and more than 10 other angles that are within one degree of each other. The difference with these additional angles is that they do not share the same radial points.

people not only fully understood what they were doing but were also fully determined and committed to the process of engraving similar motifs at a very high level of quality. The focus is on analogy because attainment of analogy was crucial in the development of modern human cognition as it is the means by which any knowledge may be applied to any other knowledge. This development was not a biological or evolutionary effect brought about by simple expansion or reconfiguration of the physical brain as is commonly taught in anthropology but was the result of what is better described as a “discovery” or “cognitive realization.” (These ideas are not the least bit esoteric because discovery and realization are two ways the brain functions in all creatures that possess a brain.).

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 78

However we choose to understand its appearance in human history, the evidence from Bilzingsleben overwhelmingly indicates that analogy and all of its accompanying benefits were in full swing at least 400,000 years ago.

Finally, apart from the obvious uses of a straight edge with increments for standard measurement as demonstrated in Figure 7.3, the Bilzingsleben engravings can also be used to measure ratios at any distance, and then immediately translate these observations into scaled reductions with radial accuracy in a manner similar to how an architect or cartographer might use a triangular scale or transit. This has already been tested in regards to the map theory of Figure 7.16.

PART II
THE EARLIEST MOTIF DUPLICATED ON TWO
SEPARATE ARTIFACTS

As with straight edge theory, the groundwork for this section was also laid out in a prior publication (Feliks 2006). The studies which compare the two motifs by precise geometric means are visually self-explanatory; however, in the next two paragraphs I will relate a few essential points from the earlier publication that are equally important in understanding the motifs as ‘deliberately-duplicated’ complex symbols.

Of utmost importance is that the positional contexts of the two motifs are quite different from each other, in fact, opposites. Specifically, the motif on Artifact 3 radiates from the end corner of the artifact, whereas the motif on Artifact 1 radiates from the center. Since the motifs are otherwise alike, this indicates deliberation of design independent from the medium, i.e. the motifs were not mere responses to the shapes of their mediums.

The similarity between these two motifs is so great as to suggest the possibility that one of them was being viewed as the other was being engraved. This would make one of the motifs either the earliest confirmed iconic representation or the earliest variation on a complex theme. It is possible that the same individual created both motifs. However, if different individuals created the motifs, then the only reasonable conclusion is that this represents communication occurring between two different people by way of a graphic symbol 320,000-412,000 years ago. Further, if different individuals created the motifs and if each used a straight edge in the process, this would suggest that not only the motifs but also the subtle skill of straight edge use itself had cultural significance at Bilzingsleben. It would support the idea explained in the Conclusion that the nature of the Bilzingsleben graphics seems more in alignment with the intellectual environment of larger societies where, for instance, straight edge use is common than what would be expected in a more survival-oriented setting such as a base camp for hunter/gatherers. As distant as this comparison may seem from Homo erectus according to the standard paradigm, I suggest that most people alive today would not be able to reproduce either motif by memory including accuracy of line length and angle

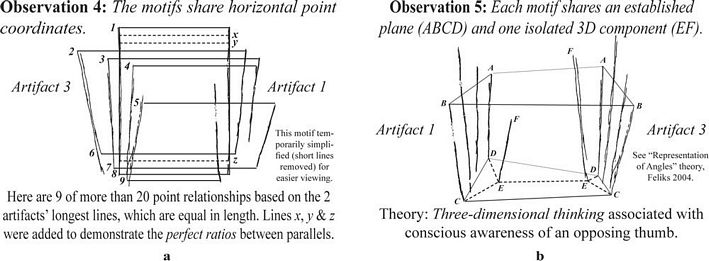Figure 6. The earliest motif duplicated on two separate artifacts, Part 2. In each of these studies, the two smallest lines of Artifact 1 have been hidden so as to make the similarities readily visible. The effects demonstrated here remain the same with or without the two smaller lines. Even though graphics are usually laid out in two dimensions, they reflect the internal world of three-dimensional thinking. 3D studies offer access to the three-dimensional mind of Palaeolithic peoples. (a) Although the two motifs appear different on the surface, when they are compared via a Cartesian grid approach, they are each seen to account for “most” of the same points, merely by different means. (The effect of how things can appear quite different on the surface yet be quite alike on a fundamental level is easy to grasp when one compares a scallop shell, for instance, with an octopus. Although completely different in external appearance they are closely related internally, and are each classified as mollusks.) (b) Comparing and interpreting two lines (each labeled EF) as positioned on “separate planes” from the other lines in each set (collectively labeled ABCD and interpreted as defining two planes).

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 79

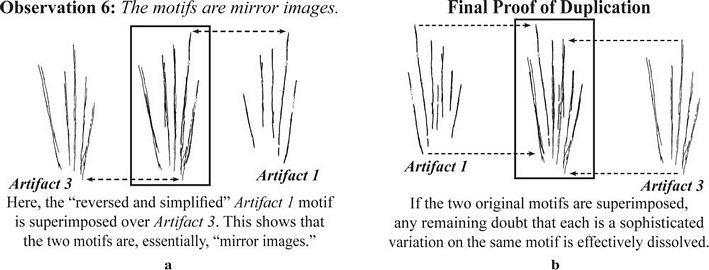Figure 7. The earliest motif duplicated on two separate artifacts, Part 3. (a) The two motifs superimposed with the Artifact 1 motif flipped in reverse. (b) The two motifs, with all lines present, superimposed according to their standard orientation. One way to test the veracity of the duplicated motif theory is to find out if any modern persons could duplicate such precision as indicated here. Computers aside, I propose that even in modern times these two motifs could not be duplicated this accurately without a straight edge or protractor and reference to the other image or its outer angle and vertex.

(as exemplified in Figs. 7.5-7.7), especially if attempting to do so with the same materials and tools originally used by Homo erectus, namely, a few bones and a flint knife.

Significance of The Earliest Motif Duplicated on Two Separate Artifacts: Duplicated motifs are the hallmark of language. Motifs duplicated with as high a degree of precision and subtle variation as those found at Bilzingsleben are likely indicative not only of language itself but of a highly-developed language. These observations are contrary not only to the idea of no language at all for Homo erectus but even with the now popular buffer-zone notion that Homo erectus may have had a form of “rudimentary” language.

PART III
350,000 YEARS BEFORE BACH: PITCH, RHYTHM, AND SYNTAX IN
HOMO ERECTUS LANGUAGE

The studies in this section were inspired by Mania and Mania’s discovery of a mathematical ratio in Bilzingsleben Artifact 2. Although the studies make use of “musical measuring systems,” for the most part, they are not about music per se. Rather; they are a brief introduction to how various rules and techniques of musical composition may be applied to understanding the language abilities and mentality of early peoples.

In their original observations, Mania and Mania noted that the engraved lines on Artifact 2 were a measurable sequence (60–20–40–40–60 mm) expressible in the ratio 3:1:2:2:3 (Mania and Mania 1988: 94). As it turns out, this ratio is remarkably transparent and can be readily compared with modern analogues. For instance, expressed in the language of musical scale degrees, the ratio and its reverse translate perfectly into two quite playable six-tone scales (Feliks 2006). The sequence of lines read according to this ratio and translated into the musical terms known as “universal key” or “universal scale” becomes 1, #2, 3, #4, #5, 7, and, in the key of C, would be played as C D# E F# G# B. This is known as “Augmented Scale X” (Kadman 1995: Fig. 46). Reading the sequence from the opposite end of the artifact, the ratio would be 3:2:2:1:3 or 1, b3, 4, 5, b6, 7, which, in classical Indian music is known as “Raga Takka.” In C, that would be played as C Eb F G Ab B. Of course, knowledge such as this does not equate to the sound of a human voice but it is a starting point for understanding early spoken language.

Another comparison quantifies in musical terms Mania and Mania’s observation that the engravings are “rhythmic” (1988: 94–5). In point of fact, the ratios translate into “exact” rhythmic units. Ratio 3:1:2:2:3, for instance, equates precisely to dotted quarter, eighth, quarter, quarter, dotted quarter, eighth. Whether we interpret these engravings literally only as per visual space or audibly in time, the nature of Artifact 2 suggests that there already existed well-developed ideas of rhythm by the time of Bilzingsleben.

BACH’S COMPOSITION TECHNIQUES AS INTERPRETATION AIDS FOR THE BILZINGSLEBEN ENGRAVINGS: Most of the ideas for this approach to Bilzingsleben are based on the author’s earlier extensive research into the musical style of J.S. Bach which included Bach’s “non-musical” influences and little-known non-musical techniques of composition (Feliks 1992, 1993, 1994). These techniques, both standard and non-standard, are applicable to

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 80

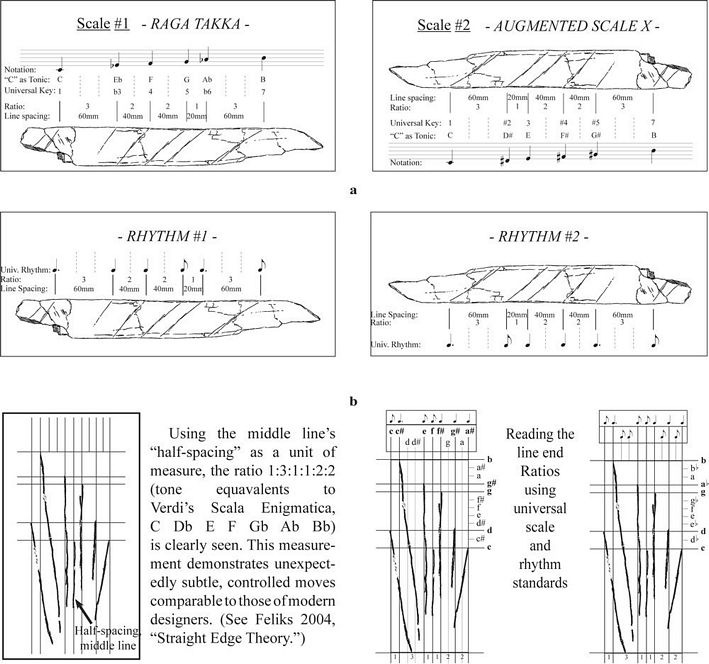Figure 8. 350,000 years before Bach. Reading the mathematical ratios by way of universal key and rhythm standards. These studies were inspired by Mania and Mania’s 1988 discovery of a mathematical ratio in the Artifact 2 engravings, namely, 3:1:2:2:3. As explained in a prior paper (Feliks 2006), these ratios are applicable to the concepts of pitch, rhythm, and syntax in Palaeothic language. (a) Artifact 2 musical scales and rhythms, only a few examples. (b) Artifact 1 side-fan motif “line end ratios,” measuring the ratios by universal key and rhythm standards. Note: spacing of vertical lines in these studies was “tempered” for easier viewing. The tolerances applied are clearly visible and are used for this interpretation only; they are not suggested as the only interpretation. The deviations are within 2%, inconsequential by archaeological standards. Side-fan motif redrawn after photograph by R. Bednarik 1997.

the Bilzingsleben engravings by means of geometric equivalents that are recognizable in the engravings. Although neither time nor space permit explaining each and every one or to point out where they may be represented in the artifacts, suffice it to say that the traits are visible in Figs. 7.2-7.14 & 7.16 of this paper and Figs. 8-11 and 16-18 of the Part 2 paper (Feliks 2008). The following paragraphs detail several of the musical techniques of Bach which are helpful in understanding the Bilzingsleben engravings.

Bach’s primary composition style is characterized by what is known as “counterpoint.” Briefly, counterpoint is a type of music in which two or more melodies are carefully constructed so as to be played simultaneously while abiding by rules of composition that can take a lifetime to master. A few examples of techniques used in counterpoint which have geometric equivalents in the Bilzingsleben engravings include: duplication of motifs (i.e. duplicating a series of notes), sequence (a pattern of notes repeating at higher or lower pitch), stretto (an

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 81

echoed phrase beginning in overlap with another), diminution (shortening phrase length), augmentation (extending phrase length), retrograde (a phrase played backwards), inversion & mirror (up notes down/down notes up), contrary motion (melodies moving in different directions), and compound line (where one melodic line may be interpreted as two). Such techniques of counterpoint and other forms of musical composition as used by Bach are clearly recognizable in the engraved artifacts of Bilzingsleben.

In addition to standard techniques of musical composition, Bach employed many “non-musical” techniques influenced by the mysticism of the Pythagoreans, Plato, etc., as well as other ancient techniques which may be regarded as artistic or poetic. As difficult to believe as it may seem at first, many of these non-musical techniques also have comparable geometric equivalents in the Bilzingsleben engravings. Since it is beyond the scope of this paper to detail the geometric equivalents of each of these techniques, suffice it to say that as far as Bach is concerned they included such as number symbolism (turning words and names, etc., into musical melodies through the use of numerology), acrostichon (writing sentences, etc., in such a way as to convey a second message if certain letters from each word are singled out and then re-combined to form new words), chiasmatism (using the Greek letter chi in various creative ways; in musical symbolism chi or X is known as Plato’s cross), and Figurenlehre (using sequences of musical notes to suggest specific human emotions, an idea inspired by techniques of rhetoric developed by Greek philosophers).

Bach also wrote “puzzle canons” in which he presented one melody to be sung as a round with up to six separate voices, but withholding the critical information of exactly when the other voices were to enter. The famous portrait of Bach in which he is holding a readable musical score shows just such a puzzle canon creating the impression of a challenge to contemporaries and future generations. In fact, one of Bach’s puzzle canons was not solved for over 100 years.

The point I am attempting to make with these comparisons is that contrary to the traditional “err-on-the-ape-side” approach in archaeology, approaching the Bilzingsleben material with the expectation that there are deeper inherent meanings to be found increases the chance that such things, if they exist, can be found. It is the approach employed in this paper. For those who may automatically question the value of such an approach, let me add that except for being contrary to the paradigm of gradually-evolving mental abilities it is no less scientific to presuppose high intelligence in early peoples than it is to presuppose low intelligence. Presupposition of low intelligence is what has brought us the concept of ape-man, which has effectively blocked our ability to understand these people on an intellectual level. Presupposition of high intelligence, on the other hand, opens up the entire world of Lower Palaeolithic mathematics and philosophy.

THE MODAL SYSTEM AND HOW IT CAN SHED LIGHT ON BILZINGSLEBEN: The modal system in music is like syntax in language where changing the order of words changes the meaning, sometimes subtly, and sometimes dramatically, as in the following three variations (see Chomsky 1972 for in-depth study of similar effects): “You go there” (1-2-3), “Go there, you” (2-3-1), “There you go” (3-1-2). In the modal system of music, completely different moods are created by shifting positions of the half and whole steps in a scale sequence of notes. In the standard C major scale or do-re-mi—C D E F G A B C—for example, the distance between any two consecutive notes in terms of whole steps and half steps (C to D is a whole step, E to F is a half step) is whole-whole-half-whole-whole-whole-half. This exact sequence may also be thought of as “Ionian mode. If we follow instead the sequence from D to D, i.e. D E F G A B C D, the sequence of whole and half steps becomes whole-half-whole-whole-whole-half-whole, otherwise known as “Dorian mode.” Dorian mode has an entirely different emotional feel and cognitive effect from that of Ionian mode even though it contains essentially the same elements. In Fig. 7.8 showing Artifact 2, the Indian scale Raga Takka is represented in the first mode, C Eb F G Ab B. If we were to duplicate the artifact only change the order of engraved lines to the second mode, Eb F G Ab B C, placing more emphasis on Eb than C, an entirely different mood would be created visually. In other words, whether or not the engravings are translated as audible sounds, a different arrangement of lines on Artifact 2 would certainly create an entirely different visual mood, and mood may be just as important a means of understanding our earliest ancestors as would be a few lines of written script.

SYNESTHESIA AND FRACTALS: Scale-like ratios such as present in Artifact 2 have the potential of visually communicating Palaeolithic ideas and emotions in a way similar to “hearing” scales after one learns the visual basics of music theory or notation. Related to this are synesthesia, where experience of one sense translates into the terms of another as exemplified by such as Feynman who saw colors in his physics equations (Feynman 2001; see also Sacks 1990, 2003), and what I have termed ‘cross-dimensional fractals’ (where a shape, pattern, or concept in one medium can be related to similar in entirely different mediums, such as a landscape being represented by a map; see also Eglash 1999 and Eglash et al. 2005 regarding scale models of African villages present as religious altars within the villages). These are all part of the normal analogical functioning of the human mind and are very useful tools for studying the engravings of Bilzingsleben. (See Harrod 2006 for a similar approach based in part on the work of abstract painter Vassily Kandinsky.)

Significance of 350,000 years before Bach: Historically, the complexities of a culture’s language tend to be reflected in the arts, including the musical arts. Therefore, it is reasonable to suggest that a complex engraved motif such as that of Bilzingsleben Artifact 2 which can be interpreted in terms of pitch, rhythm, and syntax implies

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 82

Figure 9. Fractal angle symmetry. (a) Definition of fractal, with natural world example: living fern scan (Feliks 1998). (b) Two views of Artifact 2 radial motif showing “Level 1” angles (upper image) consisting of sub-motif self-similar “Level 2” angles (lower image). Awareness of fractals is a geometric equivalent to awareness of analogy. (c) “Magnification of sub-motifs showing “Level 2” fractal angles in Artifact 2. Very notable is the engraved 3° angle. As with the 2° angle of Fig. 2a, a 3° angle is stunning by any standards. (d) “Level 1” and “Level 2” fractal angles in Artifact 2. These self-similar angles exhibit even more sophisticated variations than detailed here such as diminution and augmentation (Feliks 2008: Figures 8, 9, and 18). Most of the math regarding fractals has only been developed during the past 25 years. However, roots in ancient Africa are now known (e.g., Eglash 1999). Artifact 2 drawing after Mania and Mania 1988.

an equally complex and sophisticated spoken language. As detailed in Part IV, Artifact 2 contains not only an immediately visible surface ratio in the form of a “fan motif” but also duplicated sub-motifs of an intricate fractal nature—a technique which is also found in the work of Bach—making it a composition capable of expressing on many levels (see also Chomsky 1972 regarding deep and surface structure in language). Special Note: The double meaning title of Part III was inspired by the fact that Bach himself lived within 20-30 kilometers of Bilzingsleben.

PART IV
TOWARD THE REALM OF IDEAS: RADIAL AND FRACTAL SYMMETRIES,
INVISIBLE SHAPES

By employing extensions of engraved lines and points cognitive archaeology can access the geometric mind behind and beyond the artifacts themselves. This is possible because geometric extensions make accessible an invisible field of information outside of, but within the vicinity of, any given artifact. The extent of this field is more limited in some artifacts than in others, and the further out we go from various artifacts the more speculative the interpretations may be. However, depending on what specific information we are seeking, and despite what may be presumed, this is not necessarily the case, as suggested by Fig. 7.14, “Proof of association between an abstract point and infinity.” Depending on how the lines are organized, many interpretations of a surrounding field are perfectly safe.

Once the invisible geometric qualities are discovered and mapped out one can then genuinely access the thoughts of individuals who lived hundreds of thousands or even millions of years ago but who took the time to engrave a few lines. As difficult to believe as it may seem a vast amount of information that extends well beyond

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 83

geometry and mathematical constructs is available that easily extends into the realms of philosophy by means of geometric equivalents or ‘cross-dimensional fractals.’ This is possible because all human cognition is based upon relationships between abstract points.

Speaking only on the mathematical level, when the technique of extension is applied to Bilzingsleben, it becomes clear that Homo erectus had a developed awareness of geometry in both a standard sense (“Euclidean”) and fractal sense. In fact, the Bilzingsleben graphics are so advanced in regard to fractals (see also the Part 2 paper, Phi in the Acheulian, Feliks 2008) as to suggest a long prior development. The repeated subtleties within the repeated composite line segments of Artifact 2, for instance (Figures 7.9 & 7.11), do not in any way give one a sense of spontaneity. Rather, these particular motifs display such high refinement as to suggest a long established Acheulian knowledge system. Consider this reasoning: If the Acheulian is regarded as a million years of static technology (the standard interpretation which has long been equated with static intelligence), one could in no way expect engravings at this level of complexity and subtlety to have simply popped in out of nowhere. However, if we pursue this line of thought further and try to account for the engravings by proposing the possibility that they were all the work of a single rare Lower Palaeolithic genius (in other words, a fluke rather than representative of the general population), then a case would necessarily have to be made that, with all things considered and all things relative, this hypothetical individual would have been far more intelligent than our own da Vinci and Einstein combined. The reason I have taken this point to such an extreme is to emphasize that the most likely explanation for the advanced qualities in the Bilzingsleben engravings is that they reflect the general level that Homo erectus intelligence and culture had already attained long prior to Bilzingsleben, extending perhaps another 1.5 million years into the past, i.e. to the beginnings of the Acheulian (e.g., Gowlett 1984, 1993).

Significance of Toward the realm of ideas: As originally suggested by Mania and Mania in 1988, the people of

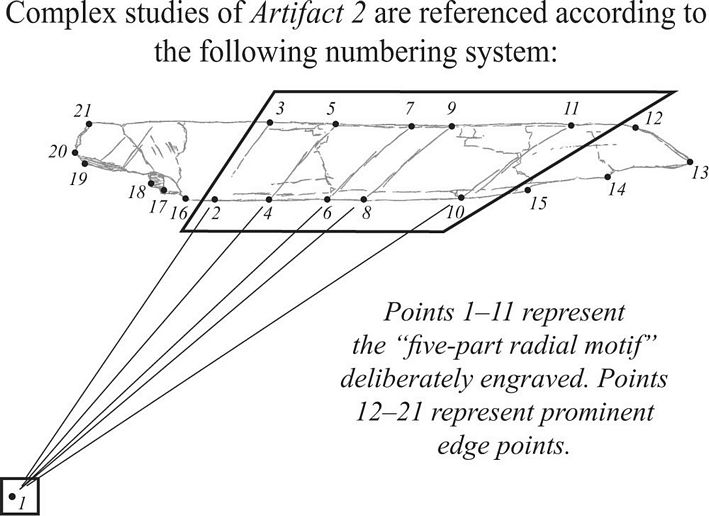Figure 10. Numbering system for the radial motif of Artifact 2. Lines which do not participate in the radial motif are not focused upon in this particular series. If the two small engraved lines at the left side of Artifact 2 are needed, their points may be referred to as 18a, 18b, and 21a, 21b.

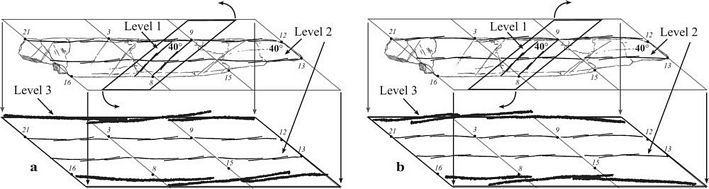Figure 11. Three-level, self-similarity fractal characterized by parallels in thirds. Interpreting components of the central double-motif as parallel rather than subtly radial, they are seen to perfectly echo the structure and basic angles of the entire artifact—whether rotated left or rotated right. Level 1 is the doubled composite motif. Level 2 is the motif duplicated three times in a row where it is seen to align perfectly with parallels 21-16, 3-8, 9-15 and 12-13. Level 3 is the double composite motif enlarged to the length of the entire artifact, at which point it is seen to still align with these very same parallels. While seeming like an inexplicable puzzle, it is simply more evidence of fractal mental structure in Homo erectus, the acceptance of which will be indispensable in understanding their language capabilities. It is notable that this interpretation works whether the motif is rotated to the left or rotated to the right. In Bach’s famous Art of the Fugue (his final work), Contrapunctus XII and XIII are known as “mirror fugues,” working equally well played forward or backward. Also, one of the mirrors is “upside-down,” while the other is a syntax inversion (see Part III). This same level of mathematical symmetry was also demonstrated by the radial motifs of Bilzingsleben Artifacts 1 & 3 (Fig. 7), that matched each other whether superimposed in standard positioning or as mirror images. (a) left rotation. (b) right rotation.

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 84

Bilzingsleben clearly had a “concept of the world.” At the time Mania and Mania suggested this, such a claim was about as far on the fringes as anyone in traditional archaeology would dare to go. It is my hope that these detailed and intricate studies of the Bilzingsleben engravings will serve not only to confirm Mania and Mania’s claim but to go much further and demonstrate that the inhabitants of Bilzingsleben had a concept of the

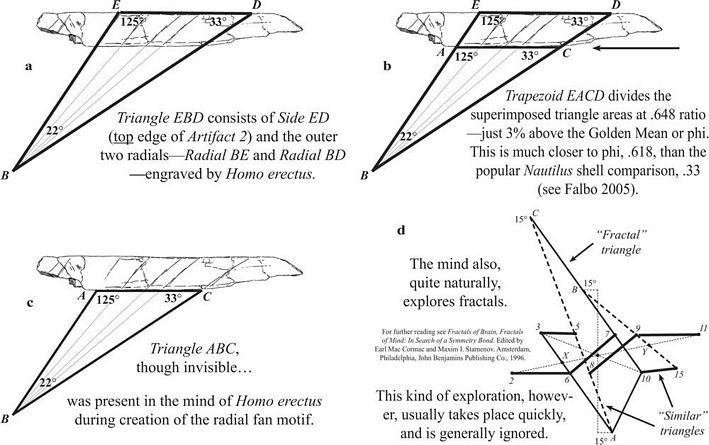Figure 12. Invisible shapes. All angle measurements are based on the original drawing by Mania and Mania 1988. (a) Radial motif of Artifact 2 pointing to invisible vertex, and defining a triangle. (b) Bottom edge of Artifact 2 divides the triangle into a smaller “fractal triangle” and a trapezoid. (c) The earliest completely abstract and measurable two-dimensional shape. (d) Excerpt from symmetric asymmetry studies. This one shows fractal extensions from the Artifact 2 central doubled motif, the same motif as in Fig. 11.

Figure 13. Proof of association between a complex graphic and an abstract point. Explanation: First, the primary engravings of Artifact 2 consist of repeating and varying composite fractal elements (see Figures 9, 11, and 14) which form a larger radial motif by way of self-similar fractal angles; this is what makes it a “complex” graphic. Second, the radial motif is traced backwards to an invisible point in space. This study suggests that the abstraction abilities necessary for complex language in which an arbitrary word stands for something which is not visually or audibly similar was already fully developed by the time of Bilzingsleben 400,000 years ago. Artifact 2 after Mania and Mania 1988.

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 85

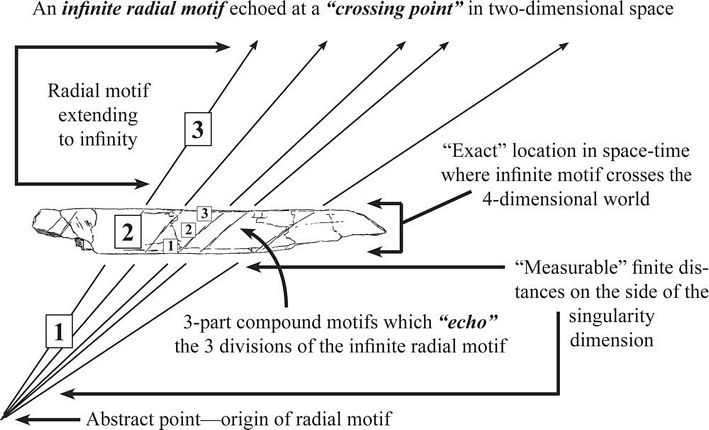Figure 14. Proof of association between an abstract point and infinity. As in the complex works of Bach, which have sometimes been described as hinting at infinite structures, the 3-part composite nature of the Artifact 2 engravings, likewise, suggest an infinite structure. Put in other terms, the fractal location of the artifact itself within the infinite radial motif is suggested by the middle segments of each 3-part composite line, which appear to have been conceived of as “breaks” in continuous radial lines, clearly “in-between” two directions of sight or thought. Conclusion: The inhabitants of Bilzingsleben were easily capable of abstract concepts at any level of complexity.

world that was not at all limited in scope. The engravings of Bilzingsleben unmistakably demonstrate that by 320,000-412,000 years ago, Lower Palaeolithic peoples were already working with advanced “ideas.” They were not only focused on their day-to-day survival needs as traditional scientific portrayals tend to suggest.

PART V
WHO WERE THE PEOPLE OF BILZINGSLEBEN? WHAT FIRE USE AND OTHER TRAITS SAY
ABOUT OUR LOWER PALAEOLITHIC ANCESTORS

The site of Bilzingsleben has been variously dated to between 320,000 and 412,000 years old (Mania and Mania 2005). The inhabitants, therefore, were contemporaries of the Homo erectus people that lived in Zhoukoudian, China, between 300,000 and 400,000 years ago. Zhoukoudian Homo erectus is also known as “Peking Man” (Fig. 7.15). The inhabitants of Bilzingsleben were similar in appearance to those at Zhoukoudian (Vlček 1978, 2002) so the skull reproduction of Fig. 7.15 may be regarded as a reasonable likeness of the people of Bilzingsleben. Not only do the Bilzingsleben and Zhoukoudian Homo erectus share physical similarities with each other but also with the Olduvai Hominid 9 Homo erectus, otherwise known as “Chellean Man,” who lived in Tanzania, Africa about 1.4 million years ago; as well as the Sangiran 17 Homo erectus who lived in Java, Indonesia about 1.7 million years ago (Vlček 1978, 2002). This similarity of appearance across such a wide geographic range effectively covers all four corners of the Lower Palaeolithic world.

Much more important, however, than physical and even genetic traits is the accumulating evidence for unifying symbolic and technological activities during the Lower Palaeolithic which includes similar stone tools and the shared technology of fire. Also, intricate bone engravings not unlike those from Bilzingsleben are known from other Lower and Middle Palaeolithic sites as well. On the level of what it actually means to be human, therefore, the presence of shared cultural traits must be considered far more important than physical appearance or genetics when it comes to either linking or distancing different human populations.

Most scholars agree that both Bilzingsleben and Zhoukoudian (not to mention many other Lower Palaeolithic sites such as Olorgesailie, Gadeb, Karari, Chesowanja, and Swartkrans, all in Africa; Yuanmou in China; L’Escale and Terra Amata in France; and Vértesszöllös in Hungary; as per Gowlett 1993: 56–7) contain abundant evidence of fire use. This is an extremely important observation when assessing the cognitive abilities and possible cultural affiliations of early peoples. The cognitive implications of the ability to create fire have been severely understated in palaeoanthropology which focuses on evolutionary distinctions and which, subsequently, necessitates finding these distinctions. Taking Gowlett’s lead, I suggest that there is

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 86

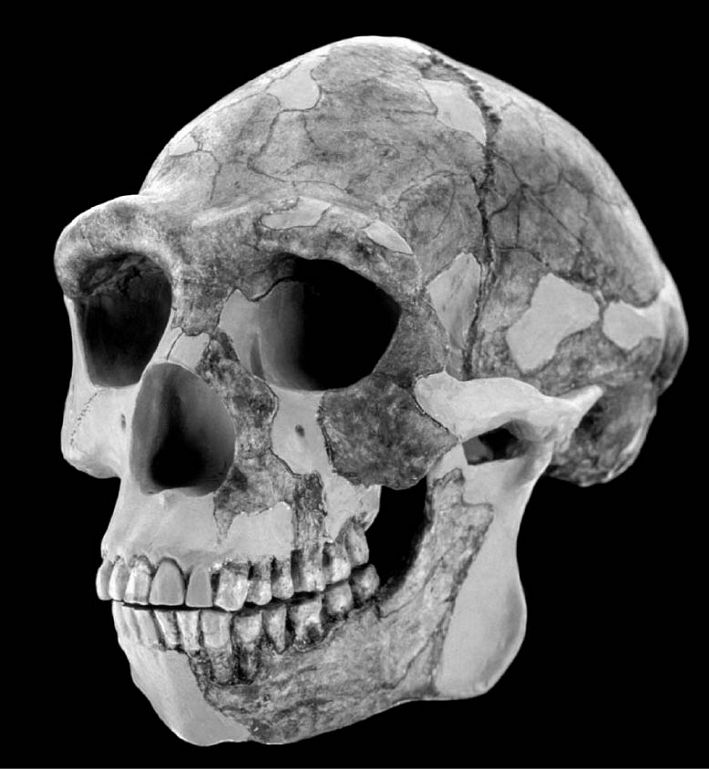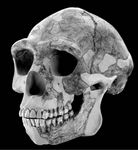
Figure 15. Who were the people of Bilzingsleben? Putting a face on the Lower Palaeolithic. In addition to their many shared cultural traits, the inhabitants of Bilzingsleben were similar in physical appearance to Homo erectus people living all over the Lower Palaeolithic world in Africa, China, and Indonesia as far back as 1.7 million years ago (Vlček 1978, 2002). This is Homo erectus from Zhoukoudian, China, also known as “Peking Man.” Skull reconstruction by I. Tattersall and G.J. Sawyer. Photograph courtesy of David Brill.

only one reason for this persistent de-emphasis. It is because what fire use actually says about the cognition of early peoples (Neanderthals included, by the way) is that they were “as intelligent” as modern humans. Our longheld belief that learning how to create fire is a sign of some transitional level of intelligence rather than completely modern intelligence is a by-product of the idea that human cognitive ability keeps evolving over time. And as Gowlett strongly hints at but does not quite say; if we accept any evidence whatsoever of higher intelligence during what are regarded as necessary-to-the theory developmental periods then the whole idea of gradual cognitive evolution collapses entirely. This is, essentially, how Gowlett accounts for the “hostility” to evidence of early fire use by some archaeologists (Gowlett 1993: 57).

In reality, fire use is a cultural trait linking all Homo erectus populations from Africa, Europe, the Middle East and Asia by way of a shared cognitive similarity. It also crosses all human time boundaries as fire use is characteristic of Neanderthals and modern Homo sapiens as well. Therefore, based on fire use alone, it is difficult to see any cognitive evolution having taken place since the earliest campfires likely created from scratch (e.g., Chesowanja, Kenya, 1.5 million years ago). Abandoning the idea of gradually-evolving intelligence in the genus Homo (as the human culture traits of long-term fire use and complex graphics suggest we should) is the key to understanding our ancestors intellectually as peers rather than as subjects of observation.

To help drive home the idea that human intelligence does not evolve, consider the following which I believe most objective persons will intuitively grasp instantly as factual without requiring any proof or testing, in other words, as a genuine axiom: If any modern Homo sapiens who had no prior knowledge of how to artificially create fire were dropped by parachute into a remote area, he/she despite their modern status would not be able to create fire even if it were necessary in order to survive. Under real-world circumstances such as this and without the aid of a supportive culture bank to inform them, even the most intelligent modern Homo sapiens individual would prove no more intelligent than the average Homo erectus. For Homo erectus and Neanderthals to have devised how to create fire in more ways than one (safely assumed), therefore, is a profound accomplishment which has been downplayed far too long.

Significance of The people of Bilzingsleben: There are two entirely unrelated schools of thought regarding early human cognitive ability and what it means to be “modern.” One is based on physical traits, and the other on symbolism or other aspects of human culture such as the use of fire. Physical anthropology, genetics, and neuroscience are telling us one story about what it means to be modern, namely, this means to be Homo sapiens; while evidence of Lower and Middle Palaeolithic symbolism is telling us a dramatically different story. The story of symbolism is far more convincing as it is based on human abilities recognizable by all people regardless of whether or not they have been specially trained. Knowledge of symbolism, fire use, etc., is what makes our shared cultural heritage accessible to everyone.

PART VI
TWO SKETCHES FROM BILZINGSLEBEN: WHEN A MAP IS
A 3D FRACTAL

Representational images are all but unknown from the Lower Palaeolithic. It would therefore seem impossible that a “map” could exist, let alone a fractal drawing (engraving) in 3D perspective. However, such capabilities are well within range of peoples now seen as capable navigators (Bednarik 1997), cooperative builders of large free standing shelters (e.g., Terra Amata, Bilzingsleben), and the makers of composite tools, necklaces and figurines (Thieme 1997, 1999, 2005; Marshack 1997). Supported by the level of cognitive ability already demonstrated in the other 5 artifacts of Bilzingsleben, I suggest that the even more complex engraving of Artifact 6 displays an image serving both as an accurate and sophisticated 3D map and a 3D perspective drawing simultaneously, each aspect done with style and a developed sense of visual impact. The confidence-of-line demonstrated in this artifact suggests the artistic flair of a confident professional graphic designer, i.e. someone who has done this type of thing many times before. This is an observation that few would question were the designer not already known to be Homo erectus. Artifact 6 (the tarsal joint bone of an extinct straight-tusked elephant) was found just 10 meters

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 87

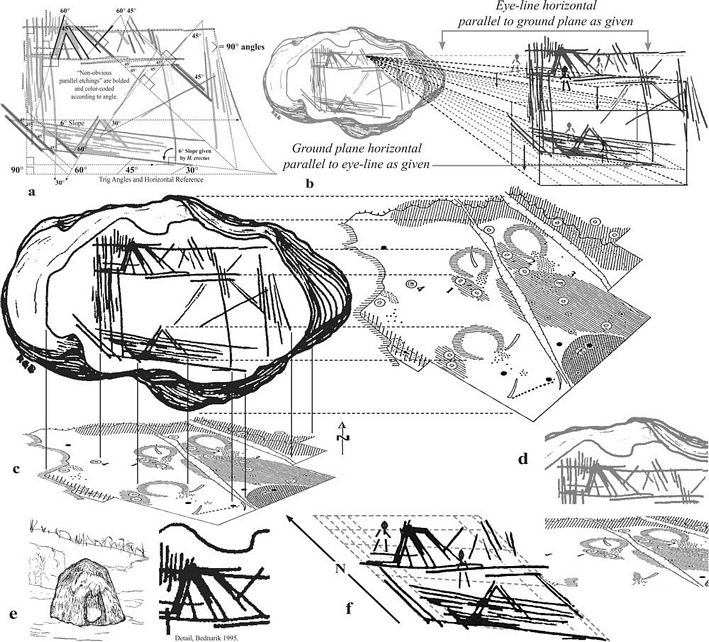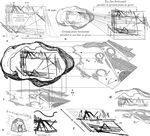
Figure 16. When a map is a 3D fractal. (a) Non-iconic interpretation of Artifact 6 demonstrates, at the very least, presence of the special trig angles 30, 45, 60, 90; parallels; diagonals; perpendiculars; and planes—all within ±3° deviation, and all likely drawn with the aid of a straight edge. Trig skills are important in surveying, mapmaking, navigation, and astronomy. (b) Seeing the planes as two tiers of a 3D map. If Artifact 6 is a map, it represents a remarkable solution by H. erectus to 3D problem. Note that the eye-line horizontal is parallel to the ground plane (as “given” by H. erectus in the lower horizontal registration notch labeled “6° Slope” in the lower right corner of the central square of Fig. 16a; parallel registration for the upper plane is visible both directly above the lower registration and to the upper left), theoretically locating the artist-cartographer in an elevated position, probably about 35 meters away from the northernmost “huts.” Ground-plane to eye-line-plane, ground-plane to observer elevation, and observer-to-huts, are measurable distances using techniques of trigonometry and a few basic assumptions. Notice other aspects of 3D perspective style including hut, ground, and angle references, depth increments (lower plane), occlusion (upper plane), and cardinal directions. (c) Comparing Artifact 6 (UPPER LEFT, Bednarik 1995) with angular views of the entire site from the shoreline south as in the original archaeological map by Mania and Mania 1988. BELOW: Site map angled to match the lower plane in Artifact 6. RIGHT: Site map angled to match the hut lines and demonstrate how the entire site is accounted for (including unanticipated nonrelief [unless the “6° Slope” and implied position of cartographer are considered] topographic features) in Artifact 6. (d) Comparing the upper plane of Artifact 6 with the two northernmost huts in the archaeological map. The map has been angled to resemble the plane suggested in the engraving. North orientation is preserved not only in the map, but in the artifact as well by way of its unambiguously engraved 90° corner. (e) LEFT: Life-size reconstruction of Bilzingsleben hut (after photo, Praehistoria Thuringica, September 2004). RIGHT: Detail from the Artifact 6 sketch perhaps by someone actually involved in the original hut’s construction, 400,000 years ago. (f) The two planes of Arfitact 6 brought to a single plane and lined up via the parallel left-right oblique “registration guides.” As a 2D map, the upper-left right angles of Artifact 6 are taken as NSEW. In the 3D interpretation, the “exactly parallel” doubled oblique registration guides are taken as NS. Remarkably, reading the artifact in this way still matches NSEW of Mania and Mania’s original archaeological map.

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 88

north of the Bilzingsleben campsite proper (Mania and Mania 2005), a fact which brings its interpretation as a map of the very same site into immediate accessibility. In fact, the location of where the artifact was found at the site can even be plotted onto the central upper tier of the artifact’s proposed 3-dimensional representational image.

As an objective courtesy, I include a plain angles study in “two” dimensions (Figure 7.16a) to demonstrate where we are going if we choose to interpret the engravings of Artifact 6 not as a map or representational drawing but rather as mere two-dimensional “scribbling.” From the perspective that Lower Palaeolithic peoples would not have been capable of representational drawing, this is as far backwards as I am willing to go in the nonrepresentational direction. Even this allegedly simpler 2D interpretation, however, still shows Artifact 6 to be one of the most sophisticated Palaeolithic artifacts yet known. In fact, given its 320,000-412,000 year-old date, the limitations of a supposedly “rudimentary” language, the medium of expression (bone), and the nature of available drafting implements (flint, bone, wood), it is as advanced as anything a modern technical designer would be capable of doing under similar circumstances.

If there is one thing that I am certain of in studying the Bilzingsleben engravings it is that they consistently express qualities analogous to the music of Bach, i.e. multiple levels of meaning. This inclines me to think that Artifact 6 was intentionally laid out to represent several perspectives simultaneously: a 2D map reflecting the campsite layout in NSEW orientation (mentally ignoring the 3D components), an accurate two-tiered 3D map, and a 3D perspective drawing to give one a sense of place, all making it a ‘cross-dimensional fractal’ in a manner similar to Artifact 2, e.g., Fig. 7.14.

There is no advantage whatsoever in interpreting the Artifact 6 engravings as “only” two-dimensional. This is because one would then have to explain the engravings in overly complex two-dimensional terms which irresistibly pull one back into 3D anyway, at which point the mind naturally settles into a relaxed state. This claim can be immediately tested simply by looking at the engraving (Figure 7.16c) and forcing oneself to see it as two-dimensional. I would compare the attempt to interpret 3D intentions as 2D to listening to a piece of music being played in a particular well-defined key (i.e. replete with tonic, sub-dominant, and dominant 7) while contrarily attempting to imagine it as though it were in a different key. In other words, certain chord combinations and progressions automatically “pull” the listener to a particular key. Could someone succeed in actually “hearing” the piece as though it were in a different key than what is obvious to everyone else? Certainly, and this kind of exercise (or technique, if one prefers) has many creative uses. However, for this type of resistance against a readily-apparent proposition in science, most traditionalists would quickly invoke Occam’s Razor—the idea that entities should not be multiplied beyond necessity. Since it takes a great deal of persistent effort to even imagine this drawing as two-dimensional, the most scientifically-sound response is to simply acknowledge rather than resist its obviously intentional three-dimensional nature.

Significance of When a map is a 3D fractal: If Artifact 6 is what it appears to be then it is the least enigmatic of all the Bilzingsleben engravings. As such, it can also quite reasonably serve as a sort of “Rosetta Stone” between our preconceptions of what intelligence in early peoples may have entailed on one extreme and the obviously sophisticated yet highly enigmatic nature of the other five engraved artifacts on the other. Also, if Artifact 6 is indeed an accurate layout map of the site, then its two-tiered system represents a remarkable solution by H. erectus to the problem of three-dimensional representation in cartography indicating extremely high intelligence. Most modern maps are abstract two-dimensional fractals (scaled representations) of object relationships in three-dimensional space (i.e. the height dimension is usually excluded), thus allowing the mapmaker to focus entirely upon only two dimensions. This is infinitely simpler than what may be represented here because even in modern times, it is no easy task to express the crucial two-dimensional information accurately while simultaneously representing the third dimension.

There is nothing at all absurd about the Bilzingsleben map proposition, wherever it may lead, or for whatever hard-to-believe capabilities it may imply. Science begins with objective observation and measurement. Apart from the studies offered in this paper, there already exist many other studies detailing the likely association between Artifact 6 and the layout of Bilzingsleben, all of which are based on openly testable evidence understandable by anyone. It is my belief that if the various archaeological maps produced by Mania and Mania over the past 20 years are accurate representations of the site, and if Artifact 6 is indeed from this very site in place and time, then there can be little doubt that Artifact 6 is a map or layout plan of the site in three dimensions. Finally, just in case the map interpretation proves not to be correct, it hardly seems to matter whether we regard this engraving as a three-dimensional map or a two-dimensional study in some basics of trigonometry; it all seems to be telling us the same thing, namely, that Homo erectus people were as intelligent and as capable as any peoples in modern historical times.

CONCLUDING THOUGHTS

About 20 years ago, Mania and Mania, the excavators of Bilzingsleben, suggested that the Homo erectus inhabitants of the site were capable of abstract thought and language and that they had a spiritual concept of the world. Although these claims may seem perfectly reasonable in light of the studies above, ideas such as these that suggest Homo sapiens-like qualities in early peoples are greatly resisted by mainstream science as they do not support the preconceived notion of gradual cognitive evolution. Homo erectus, as noted earlier, has

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 89

long played the central role of “half-way-there” link in the cognitive evolution paradigm. In this paper, I hope to have demonstrated by openly-testable empirical means not only that Mania and Mania’s interpretation of Bilzingsleben was correct from the beginning but that they actually understated it.

The geometric and representational complexity of the engraved Bilzingsleben artifacts is not anything one would expect in a survival-level environment or even in the traditional notion of a prehistoric hunter/gatherer society. Instead, it suggests an advanced cultural setting highly-supportive of pursuits unrelated to questions of survival, one that seems better matched, in fact, to a much larger society. This is especially the case if one considers the evidence offered for duplicated motifs and mathematics as most cultures that have developed anything even remotely resembling a writing system or advanced mathematical system tend to be regarded as civilizations.

While Mania and Mania’s advanced hunter/gatherer interpretation of Bilzingsleben (e.g., Mania and Mania 2005) has been difficult enough for traditional archaeology to accept, it is not at all unreasonable to point out that in modern times such an unparalleled concentration of evidence within so small an area (about 35 meters in diameter) for precision graphics which are easily readable in philosophic, linguistic, or mathematical terms would be readily identified as an academic setting of some kind. Regardless of whether or not one accepts the “academic setting” interpretation, a social environment diverse enough to inspire innovative work at the level of the Bilzingsleben engravings would certainly have been one in which artistic and academic pursuits were encouraged and held in high regard, even at this early time, 400,000 years ago. Moreover, the high degree of sophistication and innovation reflected in the six artifacts discussed does not support the idea of this being a case of sudden or isolated creativity by a single, even highly-motivated, individual; rather, it points to the presence of a larger intellectual community where there has been an exchange of similar ideas between many individuals and even between many groups of individuals for quite some time.

If Bilzingsleben represents a typical Homo erectus hunter/gatherer campsite, it is clear that early human societies were far more inclusive than traditional base level survival interpretations have long implied. From this point of view, I suggest that “hunter/gatherer campsite” and “academic setting” are two equally important and integrated aspects of early human culture that likely developed in tandem from the very beginning rather than via the unnecessary standard scenario that organized hunters and gatherers came first followed by artists and philosophers a distant second hundreds of millennia later. This latter idea, of course, is based on the single-theory mindset which has dominated Western thought ever since Darwin, the idea that humanity gradually becomes more and more intelligent over hundreds of thousands of years time. In contrast, the Bilzingsleben engravings as well as those from other Lower Palaeolithic sites represent unequivocal proof that there has been no change whatsoever in human cognitive ability for at least 400,000 years and that a great deal of reflective thought was a characteristic trait of Acheulian culture. In the Part II paper, Phi, this idea is extended back even further to the beginnings of the Acheulian.

Once we move past the idea of gradual cognitive evolution, the entire world of Lower and Middle Palaeolithic mathematics, language and philosophy opens up for us to study and learn from. This process has only begun to occur during the past 20 years or so but it promises to be a much more interesting and diverse story than we ever anticipated. In the case of Homo erectus, it is a story that involves the longest surviving and most successful group of people ever to have lived on the earth, who they actually were, and what they were capable of. The evidence is beginning to show that not only have we severely underestimated these people, but that we have done so to the highest degree imaginable. Surely, it is time to accept them as our equals.

Acknowledgments

I would like to thank the following scholars for encouragement and/or contributions to my work during the past few years. In alphabetical order: Robert Bednarik, David Brill, Noam Chomsky, Ellen Dissanayake, James Harrod, Ekkehart Malotki, Adrienne Mayor, Steven Pinker, Oliver Sacks, Raymond Tallis, and Randall White. In addition, I wish to thank my family and friends, and others who have offered support and inspiration; but I especially wish to thank the 11 sponsors who made my presentations at the XVth UISPP Congress possible.

About the author

John Feliks is an anthropology theorist specializing in the study of early human cognition. His approach is based on a long-time background in the arts and techniques of geometry and design. His recent work involves understanding the linguistic and mathematical capabilities of Homo erectus through empirical geometric studies of engraved artifacts and stone tools.

Bibliography

BEDNARIK, R.G. 1995. Concept-mediated marking in the Lower Palaeolithic. Current Anthropology 36: 605–34.

BEDNARIK, R.G. 1997. The origins of navigation and language. The Artefact 20:16–56.

BEDNARIK, R.G. 2003. The earliest evidence of palaeoart. Rock Art Research 20: 89–135.

CAPRA, F. 1982. The turning point: Science, society, and the rising culture. Simon and Schuster, New York.

PREHISTORIC ART AND SYMBOLIC BEHAVIOUR
Page 90

CHOMSKY, N. 1972. Language and mind. Enlarged Edition. Harcourt Brace Jovanovich, Inc. New York.

CORMAC, E.M. and M.I. STAMENOV (Eds.). 1996. Fractals of brain, fractals of mind: In search of a symmetry bond. Amsterdam, Philadelphia, John Benjamins Publishing Co.

DISSANAYAKE, E. 2000. Art and Intimacy: how the arts began. University of Washington Press, Seattle.

DONALD, M. 1991. Origins of the modern mind: three stages in the evolution of culture and cognition. Cambridge: Harvard University Press.

EGLASH, R., C.S. DIATTA and N. BADIANE 1998. Fractal structure in Jola material culture. Paper presented at the Congrès “Développement insulaire durable et rôles de la recherche et de la formation.” Rhodes, Greece. 277–83.

EGLASH, R. 1999. African fractals: Modern computing and indigenous design. Rutgers University Press, New Jersey.

EGLASH, R. and T.B. ODUMOSU 2005. Fractals, Complexity, and Connectivity in Africa. In G. Sica (ed.) What Mathematics from Africa? Polimetrica, International Scientific Publisher. Monza, Italy.

FELIKS, J. 1992, 1993, 1994. The Tao of Bach: J. S. Bach, mysticism, and ancient Chinese philosophy. Pp. 1–53, unpublished thesis.

FELIKS, J. 1998a. The impact of fossils on the development of visual representation. Rock Art Research 15: 109–34. (1995–97 versions submitted for publication and widely circulated).

FELIKS, J. 1998b. The value of interpretive approaches in archaeology. Rock Art Research 15: 128–29.

FELIKS, J. 2000. Iconic interface between the worlds. Comment on D. Hodgson, “Art, perception, and information processing: an evolutionary perspective.” Rock Art Research 17: 23–25.

FELIKS, J. 2003. Toward a comprehensive paradigm. Comment on Robert G. Bednarik, “The earliest evidence of palaeoart.” Rock Art Research 20: 111–14.

FELIKS, J. 2006. Musings on the Palaeolithic fan motif. In P. Chenna Reddy (ed.), Exploring the mind of ancient man: Festschrift to Robert G. Bednarik, 249–66. Research India Press, New Delhi.

FELIKS, J. 2008. Phi in the Acheulian: Lower Palaeolithic intuition and the natural origins of analogy. In BAR S1804 2008: Proceedings of the XV World Congress UISPP (Lisbon, 4-9 September 2006), Volume 19, Pleistocene Palaeoart of the World, edited by R.G. Bednarik and D. Hodgson.

FEYNMAN, R.P. 2001. What do you care what other people think? W. W. Norton and Company, New York.

GOWLETT, J.A.J. 1984. Mental Abilities of Early Man: A Look at Some Hard Evidence, in Hominid Evolution and Community Ecology: prehistoric human adaptation in biological perspective. Edited by Robert Foley. London: Academic Press.

GOWLETT, J.A.J. 1993. Ascent to civilization: The archaeology of early humans. 2nd Edition. The McGraw-Hill companies.

GREENE, B. 1999. The elegant universe: superstrings, hidden dimensions, and the quest for the ultimate theory. First Vintage Books Edition, New York.

GRUJIĆ, P.V. 2002. The concept of fractal cosmos. II: Modern cosmology. Serbian Astronomical Journal. 163: 45–66.

GRUJIĆ, P. 2006. Fractal cosmology today. Publications of the Astronomical Observatory of Belgrade 80: 67–76.

HARROD, J.B. 2006. Bhimbetka Glyphs. In P. Chenna Reddy (ed.), Exploring the mind of ancient man: Festschrift to Robert G. Bednarik, 317–328. Research India Press, New Delhi.

HAYDEN, B. 1993. The cultural capacities of Neandertals: a review and re-evaluation. Journal of Human Evolution 24: 113-46.

HREBÍCEK, L. 1994. Fractals in language. Journal of Quantitative Linguistics 1(1): 82–6.

KADMAN, A. 1995. The guitar grimoire: a compendium of formulas for guitar scales and modes. Carl Fisher, Inc., New York.

KÖHLER, R. 1997. Are there fractal structures in language? Units of measurement and dimension in linguistics. Journal of Quantitative Linguistics 4(1-3): 122–125.

LEOPOLD, E. 2001. Fractal structures in language: The question of the imbedding space. In L. Uhlirova, G. Gejza, G. Altmann, R. Köhler (eds.), Text as a linguistic paradigm: Level, constituents, constructs. Festschrift in honour of Ludek Hrebícek. pp. 163–76. Wissenschaftlicher Berlag Trier.

MANIA, D. and U. MANIA 1988. Deliberate engravings on bone artefacts of Homo erectus. Rock Art Research 5: 91–107.

MANIA, D. and U. MANIA 2003. Bilzingsleben - Homo erectus, his culture and his environment. The most important results of research. In J. M. Burdukiewicz and A. Ronen (eds.), Lower Palaeolithic small tools in Europe and The Levant. BAR S1115, pp. 29–48.

MANIA, D. and U. MANIA 2005. The natural and sociocultural environment of Homo erectus at Bilzingsleben, Germany. In C. Gamble and M. Porr (eds.), The Hominid Individual in Context: Archaeological investigations of Lower and Middle Palaeolithic landscapes, locales and artifacts, 98–114. Routledge, New York.

MARSHACK, A. 1977. The meander as a system: the analysis and recognition of iconographic units in Upper Paleolithic compositions. In Form in Indigenous Art, Prehistory and Material Culture Series, No. 13, ed. P. J. Ucko (Canberra: Australian Institute of Aboriginal Studies), pp. 286–317.

J. FELIKS: THE GRAPHICS OF BILZINGSLEBEN: SOPHISTICATION AND SUBTLETY IN THE MIND OF HOMO ERECTUS
Page 91

MARSHACK, A. 1990. Early hominid symbol and evolution of the human capacity. In P. Mellars (ed.), The emergence of modern humans: an archaeological perspective, pp. 457–98. Cornell University Press, Ithaca, N.Y..

MARSHACK, A. 1997. The Berekhat Ram figurine: a late Acheulian carving from the Middle East. Antiquity 71: 327-37.

MIKITEN, T.M., N.A. SALINGAROS, and H-S YU. 2000. Pavements as embodiments of meaning for a fractal mind. Nexus Network Journal 2: 63–74. http://www.nexusjournal.com/Miki-Sali-Yu.html. (To appear in A Theory of Architecture by Nikos A. Salingaros. Umbau-Verlag, Solingen).

MORRIS, D. 1962. The Biology of Art. Alfred A. Knopf, New York.

MORWOOD, M.J., F. AZIZ, P. O’SULLIVAN, NASRUDDIN, D.R. HOBBS, and A. RAZA. 1999. Archaeological and palaeontological research in Central Flores, East Indonesia: Results of fieldwork 1997–1998. Antiquity 73: 273–86.

OAKLEY, K.P. 1973. Fossil shell observed by Acheulian man. Antiquity 47: 59–60.

OAKLEY, K.P. 1981. Emergence of higher thought, 3.0– 0.2 Ma B.P. Philolosophical Transactions of the Royal Society of London B 292: 205–11.

POTTS, R., A.K. BEHRENSMEYER, A. DEINO, P. DITCHFIELD, and J. CLARK. 2004. Small mid-Pleistocene hominin associated with East African Acheulean technology. Science. 305: 75–8.

SACKS, O. 1990. Seeing voices: A journey into the world of the deaf. Harper Collins, New York.

SACKS, O. 1999. Migraine. Revised and expanded edition. First Vintage Books Edition, Random House, New York.

SACKS, O. 2002. Oaxaca journal. National Geographic Society, New York.

SACKS, O. 2003. A neurologist’s notebook: The mind’s eye: What the blind see. The New Yorker, July 28: 48–59.

STEGUWEIT, J. 1999. Intentionelle schnittmarken auf tierknochen von Bilzingsleben – Neue lasermikroskopische untersuchungen. Praehistoria Thuringica 3: 64–79.

THIEME, H. 1997. Lower Palaeolithic hunting spears from Germany. Nature 385: 807–10.

THIEME, H. 1999. Lower Palaeolithic throwing spears and other wooden implements from Schöningen, Germany. In H. Ullrich (ed.), Hominid Evolution: Lifestyles and Survival Strategies. Archae Edition.

THIEME, H. 2005. The lower Palaeolithic art of hunting: The case of Schöningen 13 II-4, Lower Saxony, Germany. In C. Gamble and M. Porr (eds.), The Hominid Individual in Context: Archaeological investigations of Lower and Middle Palaeolithic landscapes, locales and artifacts, 98–114. Routledge, New York.

VLČEK, E. 1978. A new discovery of Homo erectus in central Europe. Journal of Human Evolution 7:239– 51.

VLČEK, E. 2002. Der fossile mensch von Bilzingsleben – The fossil man of Bilzingsleben. In Der fossile mensch von Bilzingsleben. Bilzingsleben VI. Edited by E. Vlček, D. Mania, and U. Mania, pp. 145–392. Weissbach: Beier & Beran.

WHITE, R. 1989a “Toward a Conceptual Understanding of the Earliest Body Ornaments,” in The Emergence of Modern Humans: Biocultural adaptations in the later Peistocene. Edited by Erik Trinkaus, pp. 211– 31. Cambridge University Press.

WHITE, R. 1993. Technical and Social Dimensions of ‘Aurignacian age’ body ornaments across Europe. In Before Lascaux: the complex record of the Early Upper Paleolithic. Edited by Heidi Knecht, Anne Pike-Tag, and Randall White, pp. 277–99. CRC Press, Ann Arbor.

WHITE, R. 1993. The Dawn of Adornment. Natural History 102:60–7.