
|
Silas
Alben Professor and AIM Director Department of Mathematics 4858 East Hall 530 Church Street University of Michigan Ann Arbor, MI 48109-1043 Email: last name at umich.edu phone: 734-647-5518 |
Math 654: Introduction to Fluid Dynamics Math 501: AIM Student Seminar Course Research: My research addresses problems from biology (especially biomechanics) and engineering which can be studied with the tools of applied mathematics and continuum mechanics. My work consists of modeling, theoretical analysis and development of numerical methods, with the general goal of obtaining new physical insight into these problems. |
|
|
Membrane flutter in three-dimensional inviscid flow C. Mavroyiakoumou and S. Alben, J. Fluid Mech. (953) A32--1-38, 2022 |
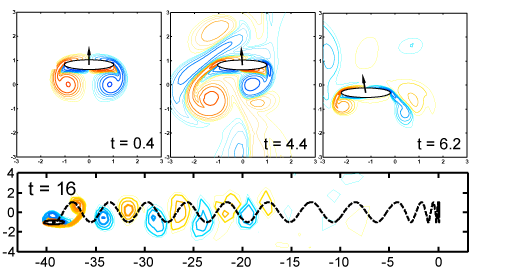
Efficient bending and lifting patterns in snake locomotion S. Alben, Proc. Roy. Soc. A (478) 20220312, 2022 |
Efficient sliding locomotion of three-link bodies with inertia A. Earnst and S. Alben, Phys. Rev. E (106) 044404, 2022 |
Packing of elastic rings with friction S. Alben, Proc. Roy. Soc. A (478) 20210742, 2022 |
Dynamics of flags over wide ranges of mass and bending stiffness S. Alben, Phys. Rev. Fluids (7) 013903, 2022 |
|
Dynamics of tethered membranes in inviscid flow C. Mavroyiakoumou and S.Alben, J. Fluids Struct. (107) 103384-1--30, 2021 |
Efficient sliding locomotion of three-link bodies S. Alben, Phys. Rev. E (103) 042414-1--18, 2021 |
|
Collective locomotion of two-dimensional lattices of flapping plates. Part 2. Lattice flows and propulsive efficiency S. Alben, J. Fluid Mech. (915) A21-1--25, 2021 |
Collective locomotion of two-dimensional lattices of flapping plates. Part 1. Numerical method, single-plate case and lattice input power S. Alben, J. Fluid Mech. (915) A20-1--28, 2021 |
Intermittent sliding locomotion of a two-link body |
Large-amplitude membrane flutter in inviscid flow C. Mavroyiakoumou and S. Alben, J. Fluid Mech. (891) A23--1-24, 2020 |
Semi-implicit methods for the dynamics of elastic sheets S. Alben, A. A. Gorodetsky, D. Kim, and R.D. Deegan, J. Comp. Phys. (399) 108952--1-17, 2019 |
Efficient sliding locomotion with isotropic friction S. Alben, Phys. Rev. E (99) 062402--1-17, 2019 |
Dynamics and locomotion of flexible foils in a frictional environment X. Wang and S. Alben, Proc. Roy. Soc. A (474) 2209:20170503--1-20, 2018 |
|
Improved convection cooling in steady channel flows |
Optimal convection cooling flows in general 2D geometries S. Alben, J. Fluid Mech. (814) 484-509, 2017 |
Enhanced convection heat transfer using small-scale vorticity concentrations effected by flow-driven, aeroelastically vibrating reeds |
Fluid–structure interactions with applications to biology W.-X. Huang and S. Alben, Acta Mechanica Sinica 32 (6): 977-979, 2016 |
Stability and scalability of piezoelectric flags X.Wang, S. Alben, C. Li, and Y.L. Young. Phys. Fluids (28) 023601-1-19, 2016 |
|
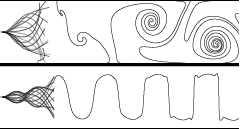 Flag
flutter in inviscid channel flow
S. Alben, Phys. Fluids, (27) 033603, 2015 Flag
flutter in inviscid channel flow
S. Alben, Phys. Fluids, (27) 033603, 2015 We determine when a straight flag in a channel-bounded inviscid flow is unstable to flapping motions. Channel confinement destabilizes heavier flags, but has little influence on lighter flags' stability. The analytical stability boundary for an infinite flag shows similar results. As the channel walls approach the flag, its flapping amplitude decreases roughly in proportion to the near-wall distance. Meanwhile, its dominant flapping frequency and wave number increase in a nearly stepwise fashion. I.e. at certain critical values of channel width, the flag jumps to a higher flapping mode. |
Passive Vibration Control of Flexible Hydrofoils using Piezoelectric Material |
  Bending
of bilayers with general initial shapes Bending
of bilayers with general initial shapes
S. Alben, Adv. Comput. Math., 2014 We present a simple discrete formulation of bilayer bending and use it to compute equilibrium configurations of actuated bilayers with general initial shapes. We identify typical bending behaviors: overall bending directions along longest and shortest dimensions, inward bending at corners, curvature intensification near boundaries, and conical bending and partitioned bending zones in some cases. |
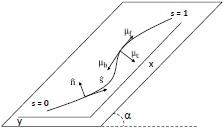 Optimizing
snake locomotion on an inclined plane Optimizing
snake locomotion on an inclined planeX.Wang, M.T. Osborne, and S. Alben, Phys. Rev. E, (89) 012717, 2014 We develop a model to study the locomotion of snakes on inclined planes. We determine numerically which snake motions are optimal for two retrograde traveling-wave body shapes, triangular and sinusoidal waves, across a wide range of frictional parameters and incline angles. In the regime of large transverse friction coefficients, we find power-law scalings for the optimal wave amplitudes and corresponding costs of locomotion. We give an asymptotic analysis to show that the optimal snake motions are traveling waves with amplitudes given by the same scaling laws found in the numerics. |
  Efficient
kinematics
for jet-propelled swimming Efficient
kinematics
for jet-propelled swimming
S. Alben, L.A. Miller, and J. Peng, J. Fluid Mech., (733) 100-133, 2013 We use computer simulations and an analytical model to study the relationship between kinematics and performance in jet-propelled jellyfish swimming. In the simulations, two types of efficient kinematics are found: a bell radius which is nearly a linear function of time, and a "burst-and-coast" kinematics. The analytical model studies the contraction phase only, and finds that the efficiency-optimizing bell radius as a function of time transitions from nearly linear for small-to-moderate output power to exponentially decaying for large output power. |
 |

 Optimizing snake locomotion in the plane S. Alben, Proc. Roy. Soc. A, 469 (2156), 2013 We determine which planar snake motions are optimal for locomotory efficiency, across frictional parameter space. With large transverse friction, our numerics and analysis show that the optimal motion is a retrograde traveling wave with amplitude scaling as the -1/4 power of the transverse friction coefficient. At zero transverse friction, a triangular direct wave is optimal. Between these extremes, we find a variety of optimal motions including standing waves (or ratcheting motions). |
 |
 |
 Functional morphology of the fin rays of teleost fishes B.E. Flammang, S. Alben, P.G.A. Madden, and G.V. Lauder, J. Morphology 2013 We examined the range of motion and curvatures of the pectoral fin rays of bluegill sunfish during steady swimming, turning maneuvers, and hovering behaviors and during a vortex perturbation impacting the fin during the fin beat. Our model showed that impacting vortices transferred little force to the fin rays due to their flexibility. This flexibility may offer intrinsic damping of environmental fluid perturbations encountered by swimming fish. |
  Optimization of two- and three-link snake-like locomotion F. Jing and S. Alben, Phys. Rev. E 87, 022711, 2013 We analyze the crawling of bodies with two and three links. The links are connected by hinge joints, and the hinge angles are actuated periodically in time. We determine the acutations which lead to the most efficient crawling motions, for different choices of coefficients of friction between the snake and the ground. High efficiency is obtained with a large backward coefficient of friction and a small transverse coefficient of friction, compared to the forward coefficient of friction. For the three-link case, the efficiency-maximizing paths are triangles in the parameter space of internal angles. |
| Using
Computational
and Mechanical Models to Study Animal Locomotion L.A. Miller, D.I. Goldman, T.L. Hedrick, E.D. Tytell, Z.J. Wang, J. Yen, and S. Alben, Integr. Comp. Biol. (2012) 52(5): 553-575 |
We review mathematical, computational, and experimental studies which compare different methods of locomotion in variable environments. A common theme of the work is applying physical principles to the understanding of living systems. |
| Passive
Robotic
Models of Propulsion by the Bodies and Caudal Fins of Fish G.V. Lauder, B.E. Flammang, and S. Alben, Integr. Comp. Biol. (2012) 52(5): 576-587 |
We discuss the use of simple robotic models of flexing fish bodies during self-propulsion. We report unexpected non-linear effects of changing the length and stiffness of the foil, and analyze the effect of changing the shape of the trailing edge on self-propelled swimming speed and kinematics. |
| Interfacing
Mathematics
and Biology: A Discussion on Training, Research,
Collaboration, and Funding L.A. Miller and S. Alben, Integr. Comp. Biol. (2012) 52(5):616-621 |
This article summarizes a workshop discussion at the 2012 Annual Meeting of the Society for Integrative and Comparative Biology on training and research at the intersection of the biological, physical, engineering, and mathematical sciences. |
  |
Dynamics
of
freely swimming flexible foils S. Alben, C. Witt, T.V. Baker, E.J. Anderson, and G.V. Lauder Physics of Fluids 24, 051901, 2012 We use modeling and simulations, guided by initial experiments, to study thin foils which are oscillated at the leading edge and are free to move unidirectionally under the resulting fluid forces. We find resonant-like peaks in the swimming speed, which is proportional to foil length to the -1/3 power and foil rigidity to the 2/15 power. |
  |
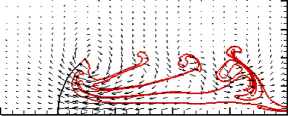 |
Effects
of
shape and stroke parameters on the propulsion performance of
an axisymmetric swimmer J. Peng and S. Alben, Bioinspir. Biomim. 2012 We consider a model jellyfish which swims by periodic body contractions, and sheds vorticity into the fluid at its outer edge according to the unsteady Kutta condition. We identify kinematic parameters which lead to swimming with high speed and small "cost of locomotion." |
| The
attraction
between a flexible filament and a point vortex S. Alben, J. Fluid Mech., 2012 A flexible filament is attracted to a point vortex when they move together as a coupled system. The point vortex collides with the filament at a finite time, with the separation distance scaling as the square root of time. We derive the power laws describing the collision. |
 |
 |
 |
Flapping
propulsion
using a fin ray S. Alben, J. Fluid Mech., 2012 We calculate optimal driving motions for a fin ray, the skeletal structure of a fin. The fin ray is driven by heaving, pitching, and a less-studied motion called "shifting." We calculate the phases of shifting relative to heaving and pitching that maximize thrust power and efficiency. |
 |
| Model
problems
for fish schooling S. Alben, IMA Volume on Natural Locomotion, 2012 |
We review recent work on model systems for body-vortex and body-body interactions in a fluid, related to fish schooling. |
| Edge
Effects
Determine the Direction of Bilayer Bending S. Alben, B. Balakrisnan, E. Smela, Nano Letters, April 29, 2011 We explain the reason for preferential bending along the long edge in thin rectangular bilayers. The bending direction is determined by the existence of doubly curved regions at the curled edges, which lower the elastic energy. Thus "spirals" are favored over "cigars." |
   |
  |
Interactions
between
vortices and flexible walls S. Alben, Int. J. Nonlinear Mech., 46, 586-591 (2011), Special issue We calculate the motion of a point vortex near a flexible wall. The vortex moves tangentially to the wall, and induces an outward "bump" on it. The force on the wall scales as the inverse cube of the distance to the point vortex, and the speed of the point vortex scales as the inverse fourth power of the same distance. |
| Self-similar
bending
in a flow: The
axisymmetric
case
S. Alben, Physics of Fluids, 22, 081901 (2010). We study how sheets roll up into conical configurations when exposed to fluid flows. We find power-law scalings for the cone angles and drag coefficients which result from a self-similar behavior of the flows at the outer edges of the cones. The similarity length scale is the radius of the vortex ring in the wake. |
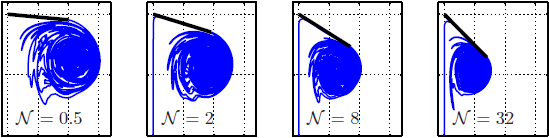 |
| Flexible sheets falling in an inviscid fluid S. Alben, Physics of Fluids, 22, 061901 (2010). Click for movie (14 Mb). | |||||
| We use inviscid simulations to study falling flexible sheets in the two-parameter space of sheet density and bending rigidity. The basic behavior is a repeated series of accelerations to a critical speed at which the sheet flexes, and rapidly decelerates, shedding large vortices. The maximum and average speeds of the sheet are closely related to the critical flutter speed. The sheet trajectories also show persistent circling, quasi-periodic flapping, and more complex repeated patterns. |      |
||||
| Coordination of multiple appendages in drag-based swimming S. Alben, K. Spears, S. Garth, D. Murphy, and J. Yen, J. R. Soc. Interface (2010). | |||||
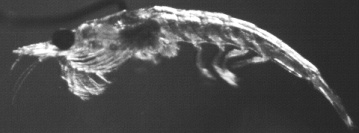 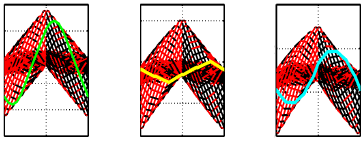 Krill are aquatic crustaceans that engage in long distance migrations. Hence efficient locomotory performance is important for their survival. Krill locomote using kinematics that are very nearly metachronal. We study a drag coefficient model which compares metachronal,synchronous and intermediate motions for a model krill. With fixed leg velocity amplitude, and with fixed output power, metachronal kinematics give the highest average body speed for both linear and quadratic drag laws. |
 |
 |
|||
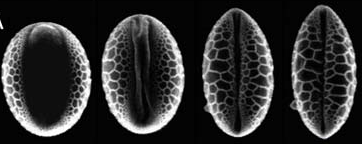
| Foldable structures and the natural design of pollen grains E. Katifori, S. Alben, E. Cerda, D.R. Nelson, and J. Dumais, PNAS, 107, 7635-7639 (2010). | |||
|
Upon release from the anther, pollen grains of angiosperm flowers are exposed to a dry environment and dehydrate. To survive this process, the pollen wall can fold inward to prevent further desiccation. Here we demonstrate that simple geometrical and mechanical principles explain how wall structure guides pollen grains toward distinct folding pathways. | 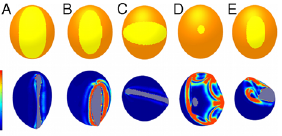 |
 |
| Regularizing
a
vortex sheet near a separation point S. Alben, Journal of Computational Physics (2010). Current methods for computing vortex sheet separation use a regularization parameter which is discontinuous from the body to the vortex sheet. We propose two methods for reducing the errors associated with the regularization parameter: the ``velocity smoothing" method and the ``tapered smoothing" method. In a model problem and a benchmark problem, both methods are found to converge much more rapidly (with exponents 3/2 and 2 versus 1/2 for the standard method) for similar computational expense. |
  |
 |
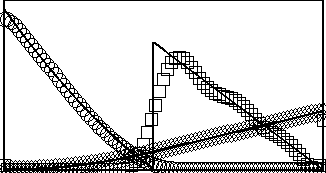
Optimizing
a
fin ray for stiffness S. Alben and R.L. McGee, Journal of the Mechanics and Physics of Solids, 58, 656-664 (2010). We optimize the elastic constants of the supporting structure in flexible fish fins--the fin ray--to obtain the least deflection under loading. We first solve the problem numerically for rays with shear layers of uniform thickness. The optimal distributions of bending and shear moduli are nonzero on disjoint regions. The numerical solution suggests the form of the analytical solution, which we obtain using calculus of variations on two intervals with continuity conditions at the interface. The deflection of the optimal ray is less than half that of the uniform ray. |
 |
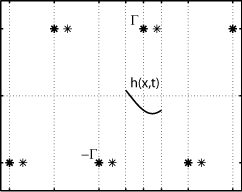
| Passive
and
active bodies in vortex-street wakes S. Alben, Journal of Fluid Mechanics, 642, 95-125 (2010). We model the swimming of a finite body in a vortex street using vortex sheets distributed along the body and in a wake emanating from its trailing edge. We consider the motion of a flexible body clamped at its leading edge in the vortex street as a model for a flag in a vortex street, and find alternating bands of thrust and drag for varying wave number. We consider a flexible body driven at its leading edge as a model for tail-fin swimming, and determine optimal motions with respect to the phase between the body's trailing edge and the vortex street. |
 |
 |
Wake-mediated
synchronization
and drafting in coupled flags S. Alben, J. Fluid Mech., 641, 489-496 (2009). Recent experiments have shown "inverted drafting" in flags: the drag force on one flag is increased by excitation from the wake of another. Here we use vortex sheet simulations to show that inverted drafting occurs when the flag wakes add coherently to form strong vortices. By contrast, normal drafting occurs for higher-frequency oscillations, when the vortex wake becomes more complex and mixed on the scale of the flag. The types of drafting and dynamics (synchronization and erratic flapping) depend on the separation distance between the flags. Movie of tandem flags, synchronized Movie of tandem flags, unsynchronized Movie of side-by-side flags |
 |
On the swimming of a flexible body in a vortex street S. Alben, Journal of Fluid Mechanics, 635, 27-45 (2009).
| We consider periodic travelling-wave swimming motions of a flexible body in a vortex street, in the limit of small amplitude. We determine the body wave which provides maximum output power for fixed amplitude and the body wave which maximizes efficiency for a given output power. We compare our results with previous experiments and simulations and give physical interpretations for agreements and disagreements in terms of the phase between the body wave and vortex street. | 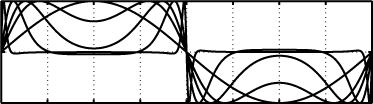 |
Collapse and folding of pressurized rings in two dimensions E. Katifori, S. Alben, D.R. Nelson, Physical Review E, 79, 056604 (2009).
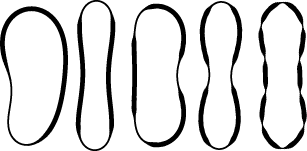 |
Hydrostatically pressurized circular rings confined to two dimensions (or cylinders constrained to have only z-independent deformations) undergo Euler-type buckling when the outside pressure exceeds a critical value. We perform a stability analysis of rings with arclength-dependent bending moduli and determine how weakened bending modulus segments affect the buckling critical pressure. Rings with a fourfold symmetric modulation are particularly susceptible to collapse. In addition we study the initial postbuckling stages of the pressurized rings to determine possible ring folding patterns. |
Simulating the dynamics of flexible bodies and vortex sheets S. Alben, Journal of Computational Physics, 228, 2587-2603 (2009) .
 |
We present a numerical method for the dynamics of a flexible body in an inviscid flow with a free vortex sheet. The formulation is implicit with respect to body variables and explicit with respect to the free vortex sheet. We apply the method to a flexible foil driven periodically in a steady stream. We give numerical evidence that the method is stable and accurate for a relatively small computational cost. A continuous form of the vortex sheet regularization permits continuity of the flow across the body's trailing edge. Nonlinear behavior arises gradually with respect to driving amplitude, and is attributed to the rolling-up of the vortex sheet. Flow quantities move across the body in traveling waves, and show large gradients at the body edges. We find that in the small-amplitude regime, the phase difference between heaving and pitching which maximizes trailing edge deflection also maximizes power output; the phase difference which minimizes trailing edge deflection maximizes efficiency. | 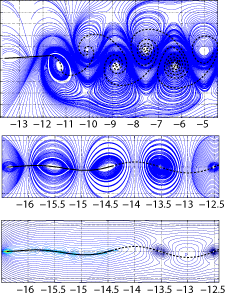 |
A cascade of length scales in elastic rings under confinement K. Spears and S. Alben, Chaos, 18, 041109 (2008).
 |
Elastic objects under confinement are common in mechanics and biology. Examples include mitochondria and chromosomes, for which conformation and function are strongly determined by confining forces. When elastic objects grow in a confined space, minimization of elastic energy creates a complex spatial configuration and force network. To simulate a two-dimensional ring growing within a rigid circular boundary with a fixed radius, we take a long strip of elastic material (mylar) of fixed length, join the ends to form a closed loop, and then shrink the confining ring boundary. We find a distribution of curvatures which is inversely proportional to the local number of overlapping layers. We give a simple quantitative argument for this relationship. |  |
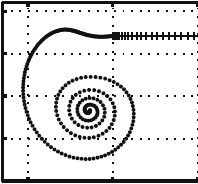
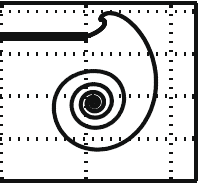
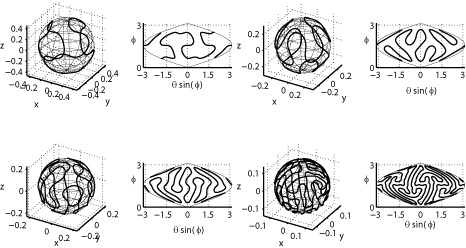
| Packings
of
a charged line on a sphere S. Alben, Physical Review E, 78, 066603 (2008). We find equilibrium configurations of open and closed lines of charge on a sphere, and track them with respect to varying sphere radius. Closed lines transition from a circle to a spiral-like shape through two low-wave-number bifurcations ("baseball seam" and "twist") which minimize Coulomb energy. The spiral shape is the unique stable equilibrium of the closed line. Other unstable equilibria arise through tip-splitting events. An open line transitions smoothly from an arc of a great circle to a spiral as the sphere radius decreases. Under repulsive potentials with faster-than-Coulomb power-law decay, the spiral is tighter in initial stages of sphere shrinkage, but at later stages of shrinkage the equilibria for all repulsive potentials converge on a spiral with uniform spacing between turns. Multiple stable equilibria of the open line are observed. |
 |
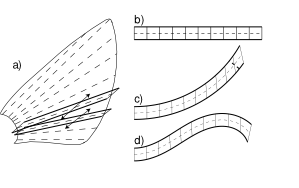
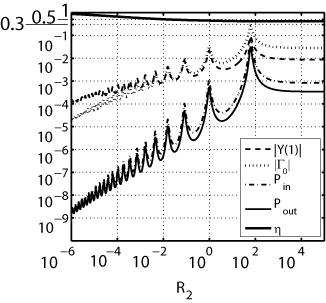
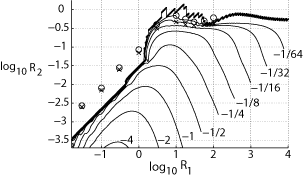
| Optimal
flexibility
of a flapping appendage in an inviscid fluid S. Alben, Journal of Fluid Mechanics, 614, 355 - 380 (2008). 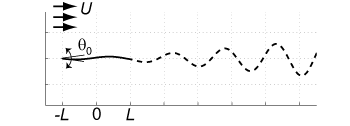 We study propulsive forces generated by a flexible body with a vortex-sheet wake pitched periodically at the leading edge. We find that the thrust power generated by the body has a series of damped resonant peaks with respect to rigidity, the highest of which corresponds to a body flexed upwards at the trailing edge in an approximately one-quarter-wavelength mode of deflection. Subsequent peaks in response have power-law scalings with respect to rigidity and correspond to higher-wavenumber modes of the body. We derive the power-law scalings by analysing the fin as a damped resonant system. In the limit of small driving frequency, solutions are self-similar at the leading edge. In the limit of large driving frequency, we find a power-law distribution of resonant rigidities. We compare these results with the range of rigidity and flapping frequency for the hawkmoth forewing and the bluegill sunfish pectoral fin. |
 |
| The
flapping-flag
instability as a nonlinear eigenvalue problem S. Alben, Physics of Fluids, 20, 104106 (2008). We reconsider the classical problem of the instability of a flapping flag in an inviscid background flow with a vortex sheet wake, and reformulate it as a nonlinear eigenvalue problem. We solve the problem numerically for the 20 lowest wave number modes in the parameter space of flag mass and flag rigidity. We study the connection between the modes and the growth rates in the eigenvalue and initial value problems. Using an infinite flag model we compute the parameters of the most unstable flag and show that a classical mechanism for the instability correlating pressure lows to flag amplitude peaks does not hold. |
 |
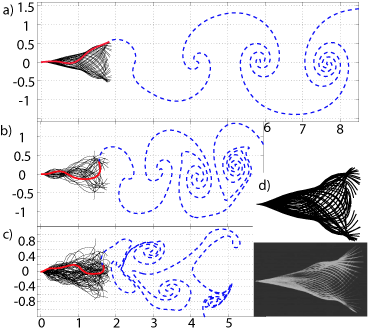 |
Flapping
states
of a flag in an inviscid fluid:
bistability
and
the transition to chaos S. Alben and M.J. Shelley, Physical Review Letters, 100, 074301 (2008). We investigate the "flapping flag" instability through a model for an inextensible flexible sheet in an inviscid 2D flow with a free vortex sheet. We solve the fully-nonlinear dynamics numerically and find a transition from a power spectrum dominated by discrete frequencies to an apparently continuous spectrum of frequencies. We compute the linear stability domain which agrees with previous approximate models in scaling but differs by large multiplicative factors. We also find hysteresis, in agreement with previous experiments. Erratum: correction of parameters and Fig. 2 Movies of Flapping Flags (.avi files): First Periodic State Second Periodic State Third Periodic State Chaotic State |
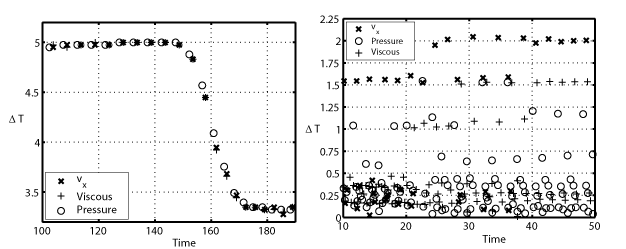
| An
implicit
method for coupled flow-body dynamics S. Alben, Journal of Computational Physics, 227, 4912--4933 (2008). We propose an efficient method for computing coupled flow-body dynamics. The time-stepping is implicit, and uses an iterative method (preconditioned GMRES) to solve the flow-body equations. The preconditioner solves a decoupled version of the equations which involves only the inversion of banded matrices, and requires a small number of iterations per time step. We use the method to probe the instability to horizontal motions of an elliptical body with simple vertical motions: flapping and rising. |
 |
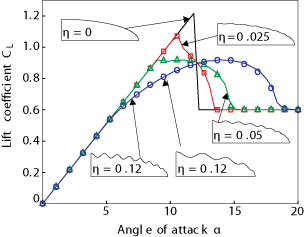
| How
bumps
on whale flippers delay stall: an aerodynamic model E.A. van Nierop, S. Alben, and M.P. Brenner, Physical Review Letters, 100, 054502 (2008). |
Wind tunnel experiments have shown that bumps on the
leading edge of model humpback whale flippers cause them to "stall" (i.e., lose lift
dramatically) more gradually and at a higher angle of attack. Here
we develop an aerodynamic model which explains the observed
increase in stall angle. The model predicts that as the amplitude of the bumps is
increased, the lift curve flattens out, leading to potentially
desirable control properties. See also: "Whale-Inspired Windmills," MIT Technology Review Mar. 6, 2008 "Fluid dynamics: Lifting a whale," Nature, Research Highlights Feb. 21, 2008 |
 |
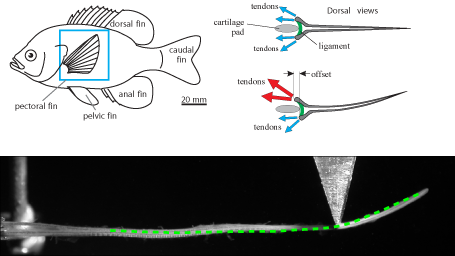
| The
mechanics
of active fin-shape control in ray-finned fishes
S. Alben, P.G. Madden and G.V. Lauder, Journal of the Royal Society Interface, 4, 243--256 (2007). We have studied the mechanical properties of fin rays, which are a fundamental component of fish fin structure. We have derived a linear elasticity model which predicts the shape of fin rays given the input muscle actuation and external loading. The model agrees well with experiments: both show a concentration of curvature at the ray base or at the point of an externally-applied force, and a variation in ray stiffness over more than an order of magnitude depending on actuation at the bases of the fin rays. |
 |
 |
The
self-assembly
of flat sheets into closed surfaces S. Alben and M.P. Brenner, Physical Review E, 75, 056113 (2007). A recent experiment (Boncheva et al. PNAS 102, 3924-3929 (2005)) introduced the possibility of initiating the self-assembly of a 3D structure from a flat elastic sheet. The ultimate utility of this method for assembly depends on whether it leads to incorrect, metastable structures. Here we examine how the number of metastable states depends on the sheet shape and thickness. Using simulations and theory we have identified out-of-plane buckling as the key event leading to metastability. The buckling strain that arises from joining edges of a planar sheet can be estimated using the theory of dislocations in elastic media. The number of metastable states increases rapidly with increasing variability in the boundary curvature and decreasing sheet thickness. See also: Self-assembly could simplify nanotech construction, New Scientist, June 7, 2007 |
| Coherent
locomotion
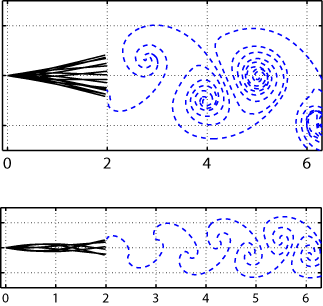
as an attracting state for a free flapping body PNAS, 2005, 102 (32), 11163-11166; S. Alben and M.J. Shelley. We study numerically a fluid flow problem at the transition between low and high Reynolds number locomotion, motivated by an experiment at the Courant Institute Applied Math Lab. In our study, a 2-D rigid body is flapped in the vertical direction and is free to move horizontally. Above a critical flapping frequency, the wing becomes unstable to horizontal motion. For certain ranges of wing shape and mass, this instability saturates to unidirectional flapping flight. We have found that the typical event which triggers "take-off" is a fortuitous collision of the body with vortices shed on previous flapping strokes. Dynamics of a free flapping body Take-off (.mov) Take-off (.avi) Back-and-forth (.mov) Back-and-forth (.avi) Chaotic (.mov) Chaotic (.avi) Thin body (.mov) Thin body (.avi) |
 |
| How
flexibility
induces streamlining in a two-dimensional flow
Physics of Fluids 16 (5): 1694-1713 (2004); S. Alben, M. Shelley, and J. Zhang Drag reduction through self-similar bending of a flexible body Nature 420, 479-481 (2002); S. Alben, M. Shelley, and J. Zhang |
|
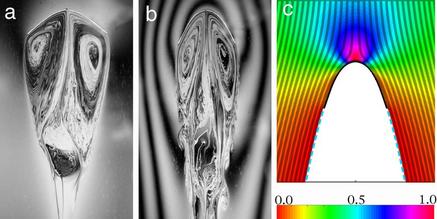 |
Nature
abounds
with organisms utilizing body flexibility in order to survive in
flowing fluids. An experiment in the Applied Mathematics
Lab at Courant studied aspects of this using a length of fiber
optic glass -- a flexible body -- immersed in the the quasi-
two-dimensional flow of a running soap film. As the flow
speed increases the shape of the flexible body bends and becomes
more and more streamlined -- the two left panels -- and
consequently the fluid drag on the body grows much more slowly
than if it were rigid. The rightmost figure shows the
numerical solution of our model of a flexible body deformed by
an surrounding flow and wake. This theory shows an
emerging self-similarity in shape arising from a balance of
fluid and elastic forces at the tip. This self-similarity
yields a new, reduced drag law where drags grows as the 4/3
power, rather than the square, of the flow velocity. See also: Nature's Secret to Building for Strength: Flexibility, New York Times, Dec. 17, 2002 |


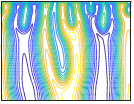




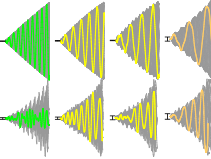
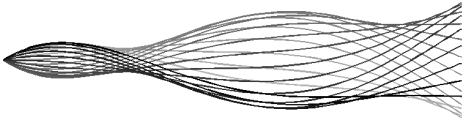
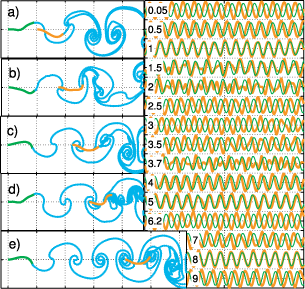
 There have been many studies of the instability of a flexible plate or flag to flapping motions, and of large-amplitude flapping. Here we use inviscid simulations and a linearized model to more generally study how key quantities—mode number (or wave number), frequency, and amplitude—depend on the two dimensionless parameters: flag mass and bending stiffness. In the limit of small flag mass, flags perform traveling wave motions that move at nearly the speed of the oncoming flow. The flag mode number scales as the −1/4 power of bending stiffness. The flapping frequency has the same scaling, with an additional slight increase with flag mass in the small-mass regime. The flapping amplitude scales approximately as flag mass to the 1/2 power. In a linearized model, the fastest growing modes have somewhat different power law scalings for wave number and frequency. We discuss how the numerical scalings are consistent with a weakly nonlinear model.
There have been many studies of the instability of a flexible plate or flag to flapping motions, and of large-amplitude flapping. Here we use inviscid simulations and a linearized model to more generally study how key quantities—mode number (or wave number), frequency, and amplitude—depend on the two dimensionless parameters: flag mass and bending stiffness. In the limit of small flag mass, flags perform traveling wave motions that move at nearly the speed of the oncoming flow. The flag mode number scales as the −1/4 power of bending stiffness. The flapping frequency has the same scaling, with an additional slight increase with flag mass in the small-mass regime. The flapping amplitude scales approximately as flag mass to the 1/2 power. In a linearized model, the fastest growing modes have somewhat different power law scalings for wave number and frequency. We discuss how the numerical scalings are consistent with a weakly nonlinear model.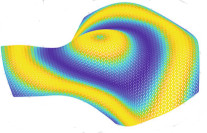 Inverse design of self-oscillatory gels through deep learning
Inverse design of self-oscillatory gels through deep learning
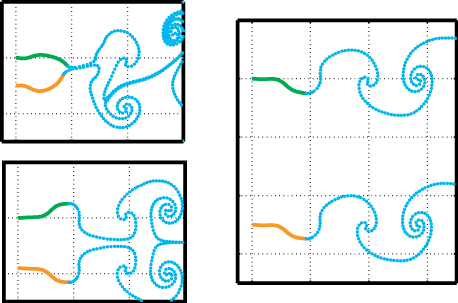
 Eigenmode analysis of membrane stability in inviscid flow
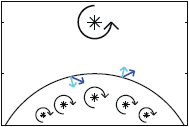
Eigenmode analysis of membrane stability in inviscid flow 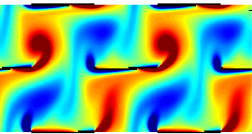 We study propulsion of rectangular and rhombic lattices of flapping plates at O(10–100) Reynolds numbers in incompressible flow. We classify the propulsive performances of the lattices and the periodicities of the flows with respect to flapping amplitude and frequency, horizontal and vertical spacings between plates, and oncoming flow velocity. Non-periodic states are most common at small streamwise spacing, large lateral spacing and large Reynolds number. Lattices that are closely spaced streamwise shed intense vortex dipoles. The flows transition sharply from drag- to thrust-producing at critical flow speeds, and pass through a variety of periodic and non-periodic states. Multiple stable self-propelled speeds can occur. As the streamwise spacing increases (and with large lateral spacing), the plates may shed vortex streets that impinge on downstream neighbors. With small lateral spacing, the rectangular lattices yield net drag, while the rhombic lattices may generate net thrust efficiently. As lateral spacing increases, the two types of flows converge. The lattices’ maximum Froude efficiencies exceed those of an isolated plate by a factor that grows with decreasing Re, exceeding two at Re = 70.
We study propulsion of rectangular and rhombic lattices of flapping plates at O(10–100) Reynolds numbers in incompressible flow. We classify the propulsive performances of the lattices and the periodicities of the flows with respect to flapping amplitude and frequency, horizontal and vertical spacings between plates, and oncoming flow velocity. Non-periodic states are most common at small streamwise spacing, large lateral spacing and large Reynolds number. Lattices that are closely spaced streamwise shed intense vortex dipoles. The flows transition sharply from drag- to thrust-producing at critical flow speeds, and pass through a variety of periodic and non-periodic states. Multiple stable self-propelled speeds can occur. As the streamwise spacing increases (and with large lateral spacing), the plates may shed vortex streets that impinge on downstream neighbors. With small lateral spacing, the rectangular lattices yield net drag, while the rhombic lattices may generate net thrust efficiently. As lateral spacing increases, the two types of flows converge. The lattices’ maximum Froude efficiencies exceed those of an isolated plate by a factor that grows with decreasing Re, exceeding two at Re = 70.  We propose a model and numerical method for the propulsion of rectangular and rhombic lattices of flapping plates at O(10–100) Reynolds numbers in incompressible flow. We use an adaptive mesh to mitigate singularities at the plates’ edges, and find convergence rates in a test problem. We then establish benchmark results for a single flapping plate, including vortex wake characteristics and Froude efficiency over ranges of flapping amplitude, frequency and Strouhal number. As a prelude to a study of propulsive efficiency in Part 2, we study a key ingredient: the time-averaged input power in lattices of plates. Scaling laws for the mean input power are estimated in the limits of small and large streamwise spacings, using steady flow models with small-gap and Poiseuille-like flows between the plates respectively in the two limits.
We propose a model and numerical method for the propulsion of rectangular and rhombic lattices of flapping plates at O(10–100) Reynolds numbers in incompressible flow. We use an adaptive mesh to mitigate singularities at the plates’ edges, and find convergence rates in a test problem. We then establish benchmark results for a single flapping plate, including vortex wake characteristics and Froude efficiency over ranges of flapping amplitude, frequency and Strouhal number. As a prelude to a study of propulsive efficiency in Part 2, we study a key ingredient: the time-averaged input power in lattices of plates. Scaling laws for the mean input power are estimated in the limits of small and large streamwise spacings, using steady flow models with small-gap and Poiseuille-like flows between the plates respectively in the two limits.  S. Alben and C. Puritz, Phys. Rev. E (101) 052613-1--20, 2020
S. Alben and C. Puritz, Phys. Rev. E (101) 052613-1--20, 2020

 Intracellular localization of nanoparticle dimers by chirality reversal
Intracellular localization of nanoparticle dimers by chirality reversal
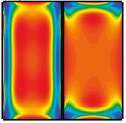
 We generalize a recent method for computing optimal 2D convection cooling flows in a horizontal layer to a wide range of geometries, including those relevant for technological applications. We write the problem in a conformal pair of coordinates which are the pure conduction temperature and its harmonic conjugate. We find optimal flows for cooling a cylinder in an annular domain, a hot plate embedded in a cold surface, and a channel with a hot interior and cold exterior.
We generalize a recent method for computing optimal 2D convection cooling flows in a horizontal layer to a wide range of geometries, including those relevant for technological applications. We write the problem in a conformal pair of coordinates which are the pure conduction temperature and its harmonic conjugate. We find optimal flows for cooling a cylinder in an annular domain, a hot plate embedded in a cold surface, and a channel with a hot interior and cold exterior.



