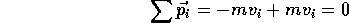
© Timothy E. Chupp, 1995
Collisions take place all the time, everywhere. Most sports played in America are based on collisions. Hitting a baseball is the collision of batter and bat with ball. Soccer requires collisions of feet and head with the ball. Hockey and football are sports for which the collisions of two or more players is as important as collisions of foot with ball or stick with puck. All materials are made up of molecules that are in constant motion and constantly colliding. We will soon analyze the motions of colliding molecules in gaseous materials.
Energy conservation and momentum conservation provide the tools necessary to consider the outcome of collisions. In most cases we will encounter systems for which the external forces are balanced so that PE does not change and conservation of momentum is useful for analyzing the collision. Since it is not necessary to account for changes in PE, it can be set to ZERO, and the total energy of the system is the sum of KE and any heat produced in the collision.
In some collisions (such as those often taking place between molecules of a gas) the total KE of the objects is constant, and no energy is converted to heat. These are called elastic collisions.
Inelastic collisions are those for which some KE is converted into heat. In a totally inelastic collision, the maximum amount of KE is converted to heat, consistent with momentum conservation.
A very straightforward elastic collision is one for which two equal mass objects are moving toward each other with velocities of equal magnitude and opposite direction. The outcome, it should be no surprise, is that after the collision, they move apart having only exchange velocities, that is the final velocity of each is just the negative of its initial velocity. Momentum conservation and conservation of KE provide two equations with two unknowns (the final velocities of each object). We can use momentum conservation for the one dimensional case as follows:
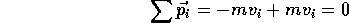
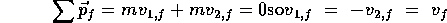
And energy conservation for the elastic collision provides
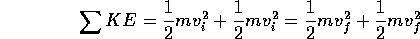
Or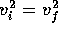 
which means that 
.
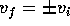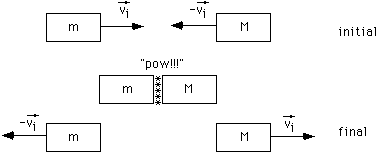
Figure 1: A special elastic collision for which two objects of equal mass initally move toward each other along a line. The result is that they exchange velocities so that the final velocity of each is the negative of its initial velocity.
This special elastic collision can be used to predict the outcome of other elastic collisions of equal mass objects by considering the collision in a moving reference frame. This is called making a transformation to a moving reference frame. Though this is not very difficult to do, it does take some getting used to, so work through this with some care.
The particular transformation we want to consider is to a frame moving to the right with
velocity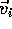 
. This is like watching the collision take place through
the window of a train moving past you. Within the train, that is in the
view of an observer on the train, the special collision described above
takes place. What does the observer on the station platform see?
We must answer this question before the collision (initial situation)
and after the collision (final situation). We'll also distinguish
the two masses as M and m.
Initial situation The mass M moving within the train at velocity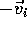 
will appear to be standing still to you observing from the platform. The mass m moving
with initial velocity 
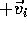will appear to be moving toward your
right with velocity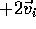 
.
Final situation After the collision, the mass M is moving in the train with
velocity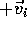 
and as observed from the platform with velocity 
,
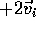and the mass m is moving in the train with velocity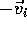 
and
as viewed from the platform with velocity ZERO.
This analysis provides the outcome of an elastic collision between two objects of equal mass when one is intially at rest. The result is they exchange velocities, and the one initially moving stops as the one initially at rest has a final velocity equal to the other's initial velocity. The "toy" called Newton's Balls provides a nice demonstration of elastic collisions of equal mass objects and the exchange of velocities.
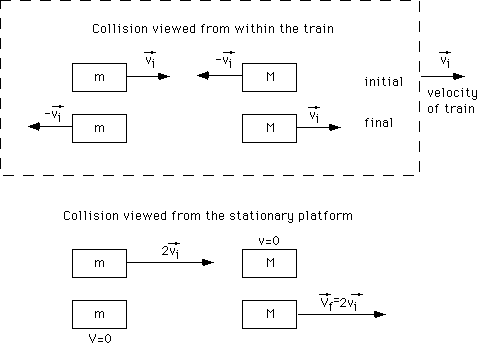
Figure 2: The special elastic collision in a moving train as viewed from the station platform.
Now we'll analyze a collision of two unequal masses, one mass M initially
at rest and the other m approaching with velocity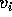 
.
Energy and momentum conservation
tell us:
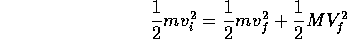
A few steps of algebra yield
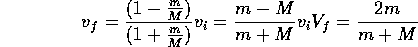
This is general result produces the results discussed above for equal mass objects when m=M, so that
Also, note that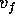 
can be positive, if m>M or negative if M<m. A smaller mass
approaching a larger mass will bounce back in a collision. If a larger mass is intially
moving toward a smaller mass, both will continue with momentum in the direction of the
intial momentum.
Elastic collisions in two dimensions must also conserve momentum and kinetic energy. Consider the case of two equal masses approaching each other with velocities of equal magnitude but not parallel. Again we can use the transformation of observing the collision in a moving reference frame, BUT the direction of the reference frame's velocity is not parallel to the initial velocities of the objects viewed from within the train.
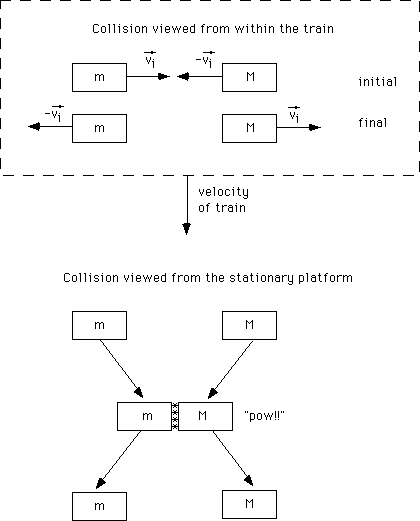
Figure 3: Two dimensional elastic collisions of two equal mass objects.
Return to Physics 125