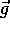 and is downward with magnitude about 9.8
and is downward with magnitude about 9.8 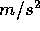 .
.
© Timothy E. Chupp, 1995
We can now use our skill with vectors in two dimensions to describe the motion
of objects that accelerate due to the influence of gravity. As we know when
the gravitational force is not balanced and air friction is neglected,
the acceleration of an object is determined by the local
gravitational field 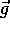 and is downward with magnitude about 9.8
and is downward with magnitude about 9.8 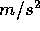 .
.
For our first example, let's describe the motion of a basketball "shot" from an initial
height of 1 meter above the ground with some initial velocity, say 8.5 m/s at 45 above
the horizontal.
First we choose a convenient coordinate system oriented such that there is no acceleration along
one axis. Thus for projectile motion in two dimensions,
one axis should be vertical (along
above
the horizontal.
First we choose a convenient coordinate system oriented such that there is no acceleration along
one axis. Thus for projectile motion in two dimensions,
one axis should be vertical (along  ) and the other
horizontal with orientation upward and toward the right positive.
The components of the velocity are
) and the other
horizontal with orientation upward and toward the right positive.
The components of the velocity are 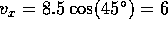 m/s and
m/s and
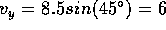 m/s.
m/s.
How do we describe the motion?
We must provide the position and velocity as time progresses.
The motion of the
basketball in the horizontal direction is not coupled to
its motion in the vertical direction. The initial horizontal velocity component is 6 m/s (to the right), the
horizontal component of its position will increase 6 m every second
regardless of how much its initial vertical velocity. And if I throw it
with an initial vertical velocity of 6 m/s, its vertical velocity will
decrease at the rate of 10 m/s every second so that after 1 second its
vertical velocity is 4 m/s and after 2 seconds its vertical velocity is
-2 m/s (2 m/s downward). This is true regardless of the horizontal velocity. Of course
the vector velocity (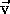 ) at any time is specified by the pair
of horizontal and vertical velocity components; and its position at
any time is specified by the pair of horizontal and vertical position
coordinates.
) at any time is specified by the pair
of horizontal and vertical velocity components; and its position at
any time is specified by the pair of horizontal and vertical position
coordinates.
One
way we have adopted is the use of strobe photographs. This shows position in two dimensions
at successive "near instants" of time. Such a strobe photo would appear like the figure.
This picture can be used to describe the motion as long as we know the interval between
flashes, which is 0.1 seconds. The average velocity for each interval can be determined from
the displacement divided by the length of the interval. For example between 0.2 and 0.3 seconds,
the second and third flashes, the displacement components are 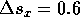 m, and
m, and 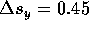 s m.
Thus
s m.
Thus 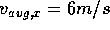 , and
, and 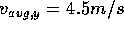 . Notice that
. Notice that 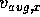 has not changed from its
initial value, because the x-component of the acceleration is zero. Of course the y-component of
has not changed from its
initial value, because the x-component of the acceleration is zero. Of course the y-component of
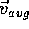 is less than its initial value, though still positive.
is less than its initial value, though still positive.
Another way to describe the motion is to provide graphs of 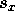 vs t,
vs t, 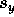 vs t,
vs t, 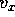 vs t, and
vs t, and
 vs t. Yet another way is to provide equations that provide
vs t. Yet another way is to provide equations that provide 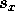 ,
, 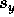 ,
, 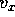 , and
, and
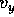 as functions of t. Remember that the equations of motion for
the components are the same as those for the vector quantity itself. We can therefore
use our tabular approach and specialize to the motion of projectiles without
air resistance:
as functions of t. Remember that the equations of motion for
the components are the same as those for the vector quantity itself. We can therefore
use our tabular approach and specialize to the motion of projectiles without
air resistance:
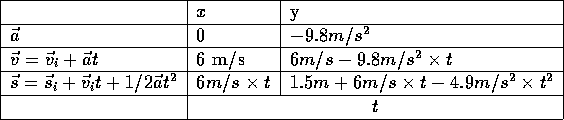
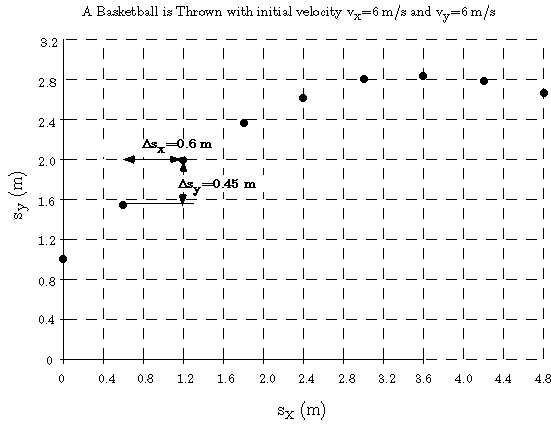
Figure 1: What a strobe photo of a basketball thrown from 1 meter high would
look like with 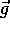 m/s at
m/s at 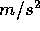 above the horizontal.
above the horizontal.
Consider the example of a basketball thrown with initial velocity
2 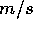 to the right (positive x direction. As an example, we may ask the following question: at what position does the basketball hit the ground if thrown from
1.5 meters high. We are therefore given
to the right (positive x direction. As an example, we may ask the following question: at what position does the basketball hit the ground if thrown from
1.5 meters high. We are therefore given 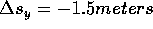 We can fill in the known quantities in the
table.
We can fill in the known quantities in the
table.
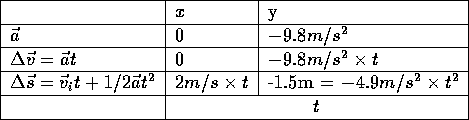
The equation for the y component of  can be solved for
can be solved for 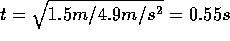 .
(Be sure to check that the units of seconds for t make sense!) We can therefore complete the table:
.
(Be sure to check that the units of seconds for t make sense!) We can therefore complete the table:

We can therefore answer the question posed: the ball hits the ground 1.5 meters below the height from which it was thrown and 1.1 meters to the right. Also, we know the velocity has changed by -5.4 m/s in the y direction, but is unchanged in the x direction.
Consider the following question: if a soccer ball is kicked at an angle of
45 above the horizontal with a velocity of magnitude 13.9 m/s, how high does
it go? To answer this, first consider that the words "how high does it go"
are translated by the physics student as "what is the y component of its
displacement when the y component of its velocity is zero, that is
above the horizontal with a velocity of magnitude 13.9 m/s, how high does
it go? To answer this, first consider that the words "how high does it go"
are translated by the physics student as "what is the y component of its
displacement when the y component of its velocity is zero, that is 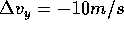 ."
Let's fill in the table with the knowledge that
."
Let's fill in the table with the knowledge that  has components
has components
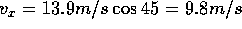 and
and 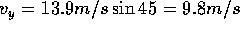 :
:
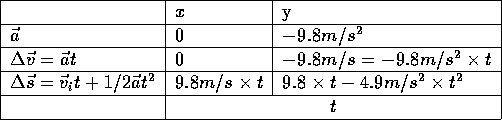
Solving 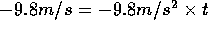 , t= 1 s and filling in the table:
, t= 1 s and filling in the table:

We also see that the horizontal displacement from the initial position to the highest point is 9.8 meters. It will take an additional second for the ball to return to the ground and therefore the distance traveled before the ball returns to the ground is 19.6 meters.
The graphical approach to kinematics problems is really the best. It is sometimes recommended to note an additional equation in one dimension derived from the constant acceleration equations by eliminating t. This equation is
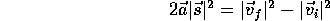
We know of course, that the description of an object's motion is incomplete because we leave out many factors such as the rotation of the earth, revolution around the sun, etc. This is a practical necessity. What we always do is describe the motion in a frame of reference which is convenient and useful for the problem at hand. Generally, we describe motion relative to a position on the earth's surface or the lecture hall. Sometimes, for example if you are in a sailing ship or on a train, motion relative to the ship or train is most appropriate. An airplane registers ground velocity and air velocity meaning velocity relative to the ground and air. Both are meaningful and important because the airplane engines and design limit air velocity, but if the air is moving, the ground velocity that affects your trip duration is different. Consider this: flying home from Europe, you are flying against the jet stream that moves the air from West to East at high altitude. In the summer, the jet stream dips south and can be hundreds of miles per hour. A 747, with air velocity of 600 miles per hour, will have a ground speed less by the jet stream velocity:, i.e. 500 miles per hour. A 3500 trip that took 5 hours West to East would take 7 hours East to West!
Relative velocities add as vectors: We would write the ground velocity of the plane with respect to the
ground ( ) in terms of its air velocity
) in terms of its air velocity 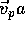 and the jet stream velocity of air with
respect to the ground (
and the jet stream velocity of air with
respect to the ground (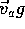 ).
).

When the plane is moving with repspect to the air in the same direction as the air with respect to the ground, the ground velocity is greater.

Figure 2: The representation of the velocity vectors of the swimmer and the
water in the stream. The resulting velocity vector of the swimmer with respect
to the bank is  m/s at
m/s at
 North of East.
North of East.
The same principles apply when there are more than one dimension. The classic example is swimming across
a stream or a current. A swimmer's velocity relative to say the bank of the stream is the sum of the
swimmers velocity with respect to the water and the water velocity with respect to the bank.
Let the stream flow north at 1 m/s and a really good swimmer capable of swimming at 2 m/s in still water.
If she heads across the stream perpendicular to the current, the resultant velocity is 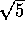 m/s = 2.24 m/s.
A typical question is a.) where does she land on the opposite bank of the 40 meter wide river
(2.24 meters
m/s = 2.24 m/s.
A typical question is a.) where does she land on the opposite bank of the 40 meter wide river
(2.24 meters  20 s = 44.8 meters downstream or North). In words we say, the velocity of the
swimmer with respect to the river bank is the sum of the vector velocity of the swimmer with respect to
the water and the vector velocity of the water with respect to the bank. Often we use the notation
20 s = 44.8 meters downstream or North). In words we say, the velocity of the
swimmer with respect to the river bank is the sum of the vector velocity of the swimmer with respect to
the water and the vector velocity of the water with respect to the bank. Often we use the notation
 referring to the vector velocity of the swimmer with respect to the water. The words
above could thus be written
referring to the vector velocity of the swimmer with respect to the water. The words
above could thus be written

This is equivalently expressed in terms of the picture representing the three vectors.
We have seen three ways to describe the physics of the motion
of objects such as basketballs and swimmers: words, the graphical
representation, and equations that express  and
and  as time passes. It is crucial to realize that these are all
equivalent, though not all equally useful in a particular situation.
A good way to practice is to express some motion you observe, invent,
or recall all three ways. Make sure that you are able to use one
description to produce the other two. Keep practicing.
as time passes. It is crucial to realize that these are all
equivalent, though not all equally useful in a particular situation.
A good way to practice is to express some motion you observe, invent,
or recall all three ways. Make sure that you are able to use one
description to produce the other two. Keep practicing.
Problem solving is a process. The process is, first THINK: what do I know about the problem and
what do I know will happen. Then express what you know in mathematical
terms
and use your knowledge of what will happen to set up the algebra.
Finally solve the equation(s).
I suggest you always construct a table like the one above.
In this case we know the initial velocity and
the accelerations and we know the ball's vertical motion will be up
and down with no net change in position BUT it will take time.
During this time it will move horizontally.
You should be able to show that the final velocity of the ball is
(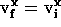 ,
, 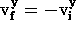 ).
).
The physical quantities position, velocity, acceleration, momentum, angular momentum, and force are vector quantities, that is they have a direction as well as a magnitude. If you can point in the direction of the quantity ( e.g. over that way) it's a vector. This pointing refers to real, three dimensional space in which you can wave your hands around. Time is not a vector quantity though you'll later hear about "The Arrow of Time." You cannot point in the direction of time! Mass and the various forms of energy are not vectors either. Time, mass and energy are often called scalar quantities. Since a vector quantity has both magnitude and direction, both must be specified. So, for velocity, you might have 25 m/s Northwest or 10 m/s to the left or 1 m/s up. In all cases, a frame of reference is necessary which is formally called a coordinate system.
We shall always use a cartesian coordinate system in one or two
dimensions. A cartesian coordinate system is one which is represented
by perpendicular axes, and is easy to draw in two dimensions as shown below.
One dimension is simply represented by a
number line which runs in the direction of the motion under consideration
i.e. up-down or horizontally across the front of the lecture hall.
For the vertical dimension, we will adopt the convention that up is in
the positive direction. Hold this sheet vertically and note that
vector 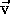 is pointed upward and is therefore positive while
vector
is pointed upward and is therefore positive while
vector 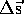 is downward and therefore the change in position
is negative.
The two dimensional coordinate system shown is appropriate for projectile motion
and, in fact, most motion can be described in two dimensions. This is fortunate
since I can't draw a three dimensional coordinate system, which I leave to your
imaginations.
The algebra of vectors includes the operations of addition and multiplication.
Addition is performed among vectors of the same quantity.
You can't
add position and velocity.
But you can add a change in position to an original position,
for example: a sailboat's original position is 10 miles NW of Rockport
and its change in position is 7 miles south. The question is, of course,
what is its final position? (7 miles west of Rockport).
The drill is as follows:
is downward and therefore the change in position
is negative.
The two dimensional coordinate system shown is appropriate for projectile motion
and, in fact, most motion can be described in two dimensions. This is fortunate
since I can't draw a three dimensional coordinate system, which I leave to your
imaginations.
The algebra of vectors includes the operations of addition and multiplication.
Addition is performed among vectors of the same quantity.
You can't
add position and velocity.
But you can add a change in position to an original position,
for example: a sailboat's original position is 10 miles NW of Rockport
and its change in position is 7 miles south. The question is, of course,
what is its final position? (7 miles west of Rockport).
The drill is as follows:
1) Choose the coordinate system, that is a set of perpendicular axes with the origin at a useful place (Rockport) and a useful orientation (North-South and West-East).
2) The original position (X marks the spot) is represented by the arrow from the origin to the X. The change in position is represented by a second arrow with appropriate magnitude and direction from the X to the dot.
3) The final position is represented by the arrow from the origin to the dot. The vector of the final position can be specified by the length and compass direction or by the cartesian coordinates (an ordered pair) of the dot. In either case, two things must be specified for our two dimensional example.
All you need to know about adding two vectors is contained in this, last,
example. There are two techniques: a graphic one which generally requires tools
like a ruler and protractor and an arithmetic one which requires
ordered pairs of coordinates
and the pythagorean theorem. The arithmetic technique is
easier to apply in practical cases while the graphic technique gives a
real picture of what's going on. Here is a summary of the arithmetic
technique for the operation  (the subscripts mean initial and final):
(the subscripts mean initial and final):
1) Pick an appropriate coordinate system.
2) Find the coordinates of  , i.e. the
ordered pair of the
point X.
, i.e. the
ordered pair of the
point X.
3) Find the coordinates of the change 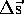 , i.e. the
change of the N-S coordinate and the change of the W-E coordinate.
, i.e. the
change of the N-S coordinate and the change of the W-E coordinate.
4) Add the N-S coordinates and the W-E coordinates. The sums make the
ordered pair of coordinates of  .
.
5) The magnitude of 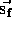 (
(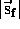 )
is given by the pythagorean theorem as
the square root of the sum of the squares of the two coordinates.
The
direction can be specified by the angle
)
is given by the pythagorean theorem as
the square root of the sum of the squares of the two coordinates.
The
direction can be specified by the angle 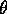 with
tan
with
tan 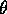 =
= 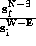 .
Other points about vector addition:
.
Other points about vector addition:
- Velocities, forces and momenta can all be added as vectors. You should think of examples of each.
- The negative of a vector is just the vector of the same magnitude pointing in the opposite direction, thus simply take the negative of each coordinate. Convince yourself that this makes sense.
- To subtract: 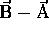 , find the negative of
, find the negative of 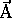 and add:
and add: 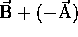 .
.
Return to Physics 125