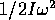. We have seen that
the work done that results in a change of the rotational energy of an
object is due to a net torque
©Timothy E. Chupp, 1995
The angular motion of an object has been characterized by it's angular velocity
and it's rotational kinetic energy 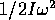. We have seen that
the work done that results in a change of the rotational energy of an
object is due to a net torque
The torque and the angular acceleration are related by the moment of inertia
:
To see that this makes sense, consider an mass on a string that constrains its motion to be a circular orbit around an axis. The instantaneous result of the torque
will be a change in the angular velocity of the object.
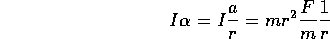
The torque produces an angular impulse which is identified with a change of the angular momentum.
Where
As we'll see, the angular momentum is a unique vector quantity that is a conserved quantity.
An orbiting mass has an angular momentum of magnitude
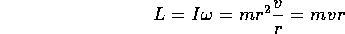
This is a special case. We can also write the vector quantity
as
where the vector or cross product of two vectors has been discussed earlier. The magnitude of
is given by
where
is the angle between
and
. Usually,
is 90
.
Angular momentum is a conserved vector quantity. For a system with no
external torque,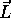 
is a constant. A nice example of this is
a spinning figure skater. A skater begins her spin with an external
torque provided by pushing off from the ice with one leg. By
spinning with a point of the skate blade planted in the ice,
very little friction dissipates the rotational energy. At the start
of the spin, the skater's arms are held outward, and a reasonable
model of the skater separates the body from the arms.
We'll model the body as a cylinder and the arms as a rod as shown in the
figure. The initial angular momentum at the start of the spin is:
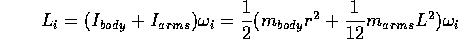
The skater can increase the angular velocity of her spin by pulling her arms (and legs) inward, thus decreasing her moment of inertia and increasing
. Notice that the quadratic dependence on the arm span
can result in a large contribution to the initial moment of inertia. When the arms are pulled inward, the large change in
results in the large change in
.
The rotational kinetic energy of the skater changes, even though her angular momentum remains constant. This means that work is done by the skater to pull her arms in. If the skater lets her arms out again to decrease
, negative work is done.
Riding a bicycle is possible because of angular momentum. The angular momentum of the wheels is a vector that remains constant unless the external torque is imbalanced. When the wheels are not turning, the bicycle and rider are in an unstable equilibrium. Any imbalance of torques leads to tipping the bicycle. Only the most skilled riders can respond in a way that dynamically maintains the bicycle upright, though not in equilibrium. When the wheels are rotating, however, tipping the bicycle by a small angle can result in a large change of angular momentum and therefore requires a large torque. For the most part, such a large torque is not supplied, and the bicycle becomes very stable when the wheels are rotating. To prove this, learn how to ride on rollers.
Another aspect of angular momentum conservation is the response of a rotating object to an external torque. The response, called precession, is that the axis of rotation twists around an axis parallel to the applied force. This makes it possible to turn a bicycle: leaning causes an external torque due to gravity resulting in the bicycle turning around a vertical axis. Lean left, the bike turns left. The greater the external torque, the greater the precession rate.
Nuclear magnetic resonance and magnetic resonance imaging (MRI) are
manifestations of precession. The nuclei of atoms have intrinsic
angular momentum, called spin. For example, the proton has
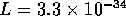kg m
/s. Associated with this nuclear
spin is a nuclear magnet arising from the charge distribution of the nucleus.
The nuclear magnet, called the magnetic moment, has its axis along
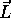(or opposite 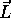). Thus an external torque, provided
by a combination of applied magnetic fields, leads to precession
of the nuclear spin and of the nuclear magnets. This is often
easily detected.
Magnetic resonance images are made by detecting the precessing
nuclear magnetism in a scanner that controls magnetic fields
position and time dependence. Most commonly, protons in tissue
are detected. However, isotopes of other elements including
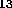C,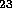 
Na and gases of 
and 
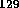Xe
are useful in scientific research.
Physics 125
This document was generated using the LaTeX2HTML translator Version 0.6.4 (Tues Aug 30 1994) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -link 0 -split 0 -no_navigation ninet.tex.
The translation was initiated by Scott D. Dexter on Tue Dec 5 16:25:22 EST 1995