© Timothy E. Chupp, 1995
We now introduce three new quantities of motion: mass, momentum
and force. We will see that momentum is characteristic of
the amount of motion of
a moving object. Changing the motion, that is the momentum, requires
an imbalance of the forces acting on that object. Mass is a property
of the object that relates that momentum to the velocity and that imbalance
of forces to the acceleration.
A good physicists' definition of mass requires us to think a bit about
the consequence of a body's mass. We all have a feel for what it means to
have more or less mass. In fact, most of us would think of a bodies weight
as the primary consequence of its mass. But weight is not a property of the
specific body alone. A particular body (say that of an astronaut) on the
surface of the moon has a different weight than on the surface of the earth
(about six times different), but the body's mass is intrinsic. Mass is a
property of any object from an elementary electron to a huge and complex
galaxy.
Weight is
not a good definition of mass. How about something like number of atoms?
This isn't convenient at any rate because it's hard to count so many atoms
(10^24 or so). But number of atoms is not a good definition for one reason
because a body with 10^{24} atoms of Carbon (C) and one with 10^24 atoms of
Lead (Pb) have very different weights even on the surface of the earth and in
fact have very different masses.
For a good definition of mass, we should consider the motion of a body as
Galileo did.
Galileo noted that an object in uniform motion (which includes zero velocity)
will change its motion only if it is subject to an imbalance of forces or a
net force i.e. a push and/or a pull. In this case,
net force is a more precise way to say an imbalance of forces,
and it means the vector sum of all the forces on the object.
Thus an object at rest on the table top will move only if the downward
pull of gravity and the upward push of the table top are accompanied by another
force such as the pull of someone's hand. The resistance to a change of
motion is called inertia and the mass of an object is a quantitative measure
of its inertia. This will be made more quantitative by Newton's second law
to be discussed later.
Imagine a ping pong ball coming at you with a velocity of 15 m/s (toward you)
(15  is about 25 mph).
To change or arrest its motion, you might catch it without much trouble.
Now imagine a bowling ball coming toward you with the same velocity.
It should be clear to your imagination that it would be a lot harder to
change its motion in the same way! The difference is not the velocity
but the difference is somehow related to the greater mass of the bowling ball.
Mass is measured in kilograms (kg). The ping pong ball has a mass of about
0.01 kg and the bowling ball about 4 kg.
is about 25 mph).
To change or arrest its motion, you might catch it without much trouble.
Now imagine a bowling ball coming toward you with the same velocity.
It should be clear to your imagination that it would be a lot harder to
change its motion in the same way! The difference is not the velocity
but the difference is somehow related to the greater mass of the bowling ball.
Mass is measured in kilograms (kg). The ping pong ball has a mass of about
0.01 kg and the bowling ball about 4 kg.
A note is in order about mass and weight. Weight only has meaning when the
device used to measure it is specified. We use a scale which generally
has a spring in it that pushes up or pulls up to balance the force of
gravity on an object. Weight is a measure
of how hard a scale must push to balance the pull of
gravity. Thus weight is the magnitude of
a force (the force balancing gravity) and has SI units of newtons and
English units of pounds (lbs.!). Mass is not a measure of force, BUT
your weight in a particular location is proportional to your mass (the
proportionality constant is g). Therefore in Europe you'll buy pate
in units of 100 gm while in the States it is sold in units of 1/4 lbs.
You may say, "1 kg weighs 2.2 lbs.", but do not say,
"1 kg is 2.2 lbs."
Momentum is a quantitative measure of the motion of an object.
There is greater total motion of the bowling ball than of the softball. Momentum
is a vector quantity defined by

Momentum is a vector quantity because it has a direction. The momentum of
an object is in the same direction as its velocity.
Note the multiplication of the vector quantity,
velocity, and the scalar quantity, mass, produces a vector quantity.
A system
of two or more objects has a total motion or momentum that is given by the vector
sum of each object's momentum. This is an important concept, because it allows
us to look at a very complicated combination of objects in motion in a very
simple way. As examples, recall the complexity of motion following the
break of the pool rack after the cue ball hit the 15 other balls or
the motion of a large number of molecules of air within a balloon.
There really is a significance to the total momentum of all those objects in
each system because it is governed by the law of Conservation of Momentum.
A force is a push or a pull. We all know how it feels to apply a force
to an object, for example to suspend a bowling ball or to push
an automobile. An imbalance of
forces is required to change the momentum of an object. To be more precise
the imbalance of forces is equal to the rate of change of momentum i.e.
for a constant imbalance of forces

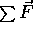 or
or  is a precise way of expressing the imbalance
of forces and is the vector sum of all the forces acting on an object.
is a precise way of expressing the imbalance
of forces and is the vector sum of all the forces acting on an object.
In order to quantify force, we'll make use of spring scales as handles
to push or pull. The scale works because a spring generally stretches
proportionally to the force applied to it (or equivalently it applies).
The spring scales
are expected to be calibrated in units of newton (N) and 2 N will be indicated by
extension or compression of the spring twice as long as that for 1 N.
Imagine pulling on
a rope attached to a box of books sitting on a rough floor. The force you apply to the
rope results in a force applied to the books by the rope. This is, of course, not the
only force on the box of books. Other forces are gravity, pulling downward and
the floor pushing upward, which is called the normal force. Some combination
of the floor's upward normal force and the upward component of the force exerted
on the books by the rope balance the force of gravity. If the box is
not moving, i.e. it is in uniform motion with constant momentum,
the horizontal force exerted on the books by the rope must also be balanced
by another horizontal force. This other force is friction, which is just
strong enough to balance the force of the rope. In order to get the box
of books moving, the rope must pull on the box with a horizontal force
greater than the maximum force of friction. Usually, once such a box
is moving, the frictional force is less than this maximum static friction
force. When the box is moving with a constant velocity and momentum, the
forces are once again balanced: The floor and rope push and pull upward to
balance the downward pull of gravity, and the horizontal force of the rope
balance the retarding force of friction.

Figure 1: A Free body diagram for the box of books.
We can imagine doing the following experiments
and noting the outcomes:
1. A 1 kg mass is accelerated at 1 m/s on the air track and the
force required is found to be 1 N (in the direction of the acceleration).
on the air track and the
force required is found to be 1 N (in the direction of the acceleration).
Since the air track pushes up on the mass to balance the force of gravity and
there is no friction, the net, unbalanced force on the mass is 1 N.
2. The 1 kg mass is accelerated at 2 m/s on the air track and the force
is found to be 2 N. At 5 m/s
on the air track and the force
is found to be 2 N. At 5 m/s , the force is found to be 5 N.
, the force is found to be 5 N.
3. The 1 kg mass is hung from the spring scale and remains stationary.
The force is 9.8 N. In this case, there is no acceleration so the net
force is zero, i.e. the force of gravity is balanced by the upward
pull of the scale. The force exerted by the spring scale must therefore
be equal in magnitude, though opposite in direction to the force exerted by
gravity. (In fact the mass is being weighed, and the weight is 9.8 N.)
If the mass were pulled along the airtrack with this force, what would
its acceleration be?
4. The previous experiment is performed in an elevator. While the elevator is
accelerating upward at 2 m/s , the force is 11.8 N. While the elevator is
accelerating downward at 3 m/s
, the force is 11.8 N. While the elevator is
accelerating downward at 3 m/s , the force is 6.8 N.
, the force is 6.8 N.
5. Each of the preceeding experiments is performed with a mass of 2 kg and
5 kg and the force is found to be respectively
2 times and 5 times that for the 1 kg mass.
In the previous experiments, the 1 kg mass accelerated only if a net, unbalanced
force was exerted. If there existed such a net force, the acceleration, the mass
and the force are related as follows:
 .
.
Let's make sure this is the case for each experiment. In 1.), the unit of
force 1 Newton is defined as the net force exerted on 1 kg accelerating at
1 m/s .
From 2.) we see that this force is proportional to the acceleration and from
5.) that it is proportional to the mass.
.
From 2.) we see that this force is proportional to the acceleration and from
5.) that it is proportional to the mass.
Experiment 3.) is different. In this case, we are measuring the force needed
to balance the force of gravity and so the net force is the vector
sum of gravity and that of the scale:
 . Since gravity
pulls down and the scale pulls up, we can express this in terms of
the components in the vertical direction as
. Since gravity
pulls down and the scale pulls up, we can express this in terms of
the components in the vertical direction as
 and note that
and note that  .
Finally, as expected, we have
.
Finally, as expected, we have  . The force
of gravity is therefore 9.8 N, 19.6 N and 49 N respectively
for the 1 kg, 2 kg and 5 kg masses, that is 9.8 m/s
. The force
of gravity is therefore 9.8 N, 19.6 N and 49 N respectively
for the 1 kg, 2 kg and 5 kg masses, that is 9.8 m/s times the mass.
times the mass.
 = mg (g = 9.8 m/s
= mg (g = 9.8 m/s
 10 m/s
10 m/s ).
).
From the relationship of force, mass and
acceleration, what would be the accelerations of these three masses if the
spring scale were removed?
The experiment 4.), performed in the elevator relates to your experience.
When the elevator starts upward, you feel a bit "heavier" as it
accelerates and as it starts downward, you feel a bit "lighter."
We can now consider this quantitatively:  where
where  is either 2 m/s
is either 2 m/s upward or 3 m/s
upward or 3 m/s downward.
Let's solve for
downward.
Let's solve for 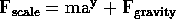 . For the 1 kg mass
accelerating upward at 2 m/s
. For the 1 kg mass
accelerating upward at 2 m/s ,
,  = 9.8 N and
= 9.8 N and
 = 2 N + 9.8 N = 11.8 N. For the mass accelerating downward
at 3 m/s
= 2 N + 9.8 N = 11.8 N. For the mass accelerating downward
at 3 m/s (a
(a = -3 m/s
= -3 m/s ),
),
 = -3 N + 9.8 N = 6.8 N.
= -3 N + 9.8 N = 6.8 N.
Return to Physics 125
 is about 25 mph).
To change or arrest its motion, you might catch it without much trouble.
Now imagine a bowling ball coming toward you with the same velocity.
It should be clear to your imagination that it would be a lot harder to
change its motion in the same way! The difference is not the velocity
but the difference is somehow related to the greater mass of the bowling ball.
Mass is measured in kilograms (kg). The ping pong ball has a mass of about
0.01 kg and the bowling ball about 4 kg.
is about 25 mph).
To change or arrest its motion, you might catch it without much trouble.
Now imagine a bowling ball coming toward you with the same velocity.
It should be clear to your imagination that it would be a lot harder to
change its motion in the same way! The difference is not the velocity
but the difference is somehow related to the greater mass of the bowling ball.
Mass is measured in kilograms (kg). The ping pong ball has a mass of about
0.01 kg and the bowling ball about 4 kg.


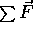 or
or  is a precise way of expressing the imbalance
of forces and is the vector sum of all the forces acting on an object.
is a precise way of expressing the imbalance
of forces and is the vector sum of all the forces acting on an object.

 on the air track and the
force required is found to be 1 N (in the direction of the acceleration).
on the air track and the
force required is found to be 1 N (in the direction of the acceleration).
 on the air track and the force
is found to be 2 N. At 5 m/s
on the air track and the force
is found to be 2 N. At 5 m/s , the force is found to be 5 N.
, the force is found to be 5 N.
 , the force is 11.8 N. While the elevator is
accelerating downward at 3 m/s
, the force is 11.8 N. While the elevator is
accelerating downward at 3 m/s , the force is 6.8 N.
, the force is 6.8 N.
 .
.
 .
From 2.) we see that this force is proportional to the acceleration and from
5.) that it is proportional to the mass.
.
From 2.) we see that this force is proportional to the acceleration and from
5.) that it is proportional to the mass.
 . Since gravity
pulls down and the scale pulls up, we can express this in terms of
the components in the vertical direction as
. Since gravity
pulls down and the scale pulls up, we can express this in terms of
the components in the vertical direction as
 and note that
and note that  .
Finally, as expected, we have
.
Finally, as expected, we have  . The force
of gravity is therefore 9.8 N, 19.6 N and 49 N respectively
for the 1 kg, 2 kg and 5 kg masses, that is 9.8 m/s
. The force
of gravity is therefore 9.8 N, 19.6 N and 49 N respectively
for the 1 kg, 2 kg and 5 kg masses, that is 9.8 m/s times the mass.
times the mass.
 = mg (g = 9.8 m/s
= mg (g = 9.8 m/s
 10 m/s
10 m/s ).
).
 where
where  is either 2 m/s
is either 2 m/s upward or 3 m/s
upward or 3 m/s downward.
Let's solve for
downward.
Let's solve for 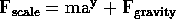 . For the 1 kg mass
accelerating upward at 2 m/s
. For the 1 kg mass
accelerating upward at 2 m/s ,
,  = 9.8 N and
= 9.8 N and
 = 2 N + 9.8 N = 11.8 N. For the mass accelerating downward
at 3 m/s
= 2 N + 9.8 N = 11.8 N. For the mass accelerating downward
at 3 m/s (a
(a = -3 m/s
= -3 m/s ),
),
 = -3 N + 9.8 N = 6.8 N.
= -3 N + 9.8 N = 6.8 N.