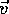) is accelerating and the rate of change of
velocity is needed to completely describe its motion.
Acceleration is the rate of change of velocity, and the average acceleration
during an interval is
© Timothy E. Chupp, 1995
Motion characterized by a straight line on the graph of position versus time, is a special case of motion called uniform motion. Uniform motion is the natural state of an object -- to change an object's motion requires an imbalance of the forces pushing and pulling on the object. For example, an air cart at rest is in uniform motion with the pull of gravity balanced by the upward force of the cushion of air. To change the motion, I give it a push, momentarily providing an imbalance of forces. Afterwards, it is moving, again with roughly uniform motion.
An object with changing velocity (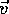) is accelerating and the rate of change of
velocity is needed to completely describe its motion.
Acceleration is the rate of change of velocity, and the average acceleration
during an interval is
Acceleration, like velocity, is a vector. The velocity of an apple, initially at rest, just after the force holding it up is suddenly removed at a point 6 m above the floor of the lecture hall is shown in the graph below. This measurement might be made with a Doppler Radar gun. In this case the motion is not uniform. What are the forces exerted on the apple which is responsible for this non-uniform motion? During successive time intervals, the velocity is negative just like the change of position (since I've chosen the starting point for my position measurements to be the floor and positions above the floor are called positive positions).
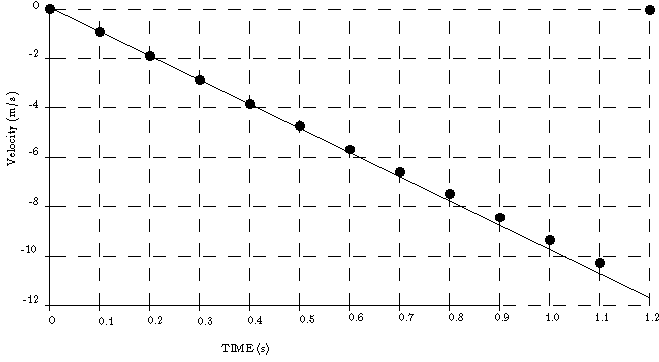
Figure 1: The velocity of a falling apple, initially at rest.
The dots representing measurements made at 0.1 second intervals show a realistic example
of air resistance which is not eliminated, say by performing the experiment in an evacuated
tube. The straight line is idealized, and is an accurate representation of what
would be measured in the absence of air resistance. The slope of this line
is the rate of change of the apple's velocity, that is the average acceleration
over the interval. For an evacuted tube, this would be very close to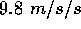 
Downward, usually written
when upward is considered the positive direction.
(The minus sign indicates the opposite of up, that is down.)
We will generally consider time intervals (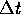
) during which the motion of
an object undergoes constant acceleration. No acceleration 
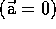during an interval
is a special case of constant acceleration. The value 9.8 m/s/s = 9.8 Newtons/kg
is the value of the gravitational field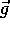 
at the surface of the earth. The gravitational
field will be discussed later, but note that its magnitude is labeled g and that if the only
force exerted on an object is the gravitational force, the objects acceleration identically
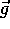with magnitude 
.
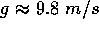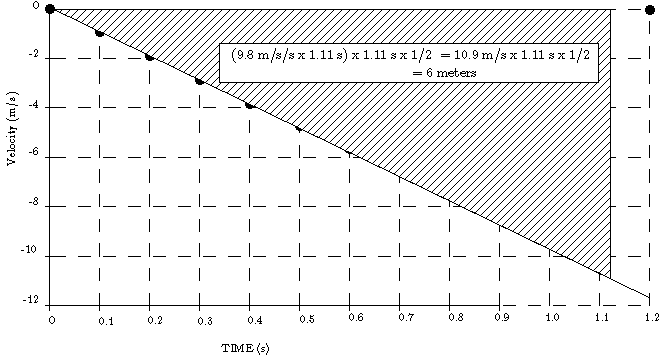
Figure 2: The area under the curve of velocity versus time is the displacement.
The rule that the displacement is given by the area under the velocity versus time curve is easily
applied for the case of constant acceleration. If the acceleration is non-zero and the velocity
is initially zero, the curve traces out a triangle with area given by one half the base times
the height. The base
is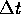 
and the height is the change of velocity
For constant acceleration with intial velocity zero, the displacement is
We therefore predict and expect that the position will change quadratically with time and trace a parabola on a position versus time graph.
The direction of the acceleration is always down whether the object is moving upward or downward. This turns
out to be one of the most difficult concepts for students of motion. Let me try to illustrate that the
upward path of an object and the downward path after it has reached
the apex of its journey have exactly the same rate of change of velocity. To do this, we look at strobe
photos of the motion. Recall that the strobe photo includes many "instants" of time and we can use
it to determine the distance traveled in the interval between flashes. What is crucial is to realize
that it is impossible to tell from the strobe photo, whether an object is moving upward after being thrown,
or moving downward after passing the apex of its flight. Recall that it is also impossible to tell which way
an object in uniform motion is moving. Use the position and velocity versus time graphs for an object thrown
upward with some initial velocity to determine the acceleration. It is constant and negative, i.e. -9.8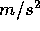 
.
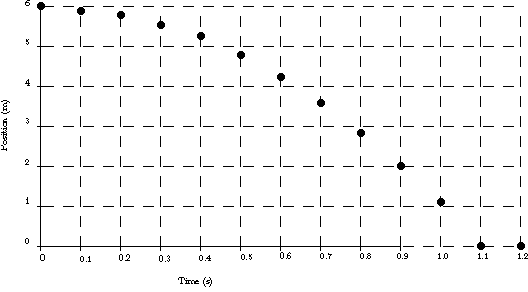
Figure 3: The velocity of a falling apple, initially at rest.
For a non-zero initial velocity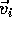 
the area under the curve would be different by the area
of the rectangle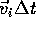 
, and the complete set of equations describing the motion of
an object with constant acceleration
is:
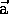= constant
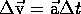
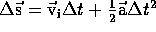
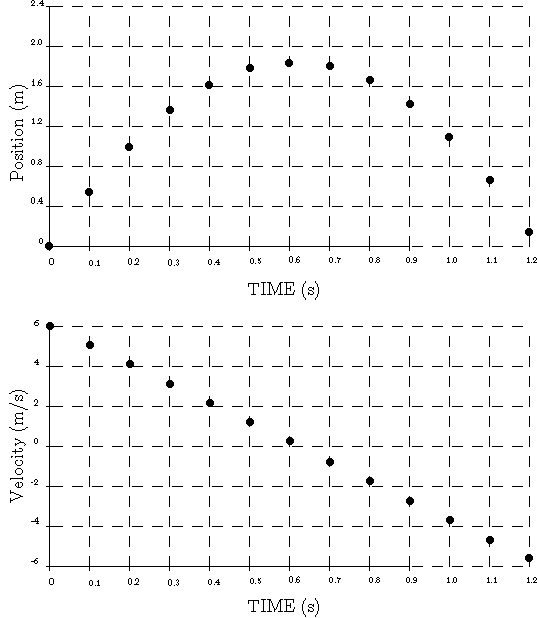
Figure 4: The position and velocity versus time for an object thrown directly upward.
We'll encounter three cases of one dimensional motion:
1) Horizontal motion with no acceleration: 
(to the right)
2) Vertical motion with acceleration due to gravity: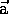 
= -g (up)
3) Motion along an incline with acceleration due to gravity and the
presence of the plane: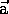 
= -g sin
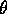(up the plane).
I was very careful to remember that acceleration is a vector and to specify the direction, in spite of the one dimension. Also note that -g (up) = g (down), but we have established the convention that up and to the right are the directions of increasing value.
A note about directions: The physical quantities which are vectors
( e.g.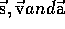 
have directions
even in one dimension. The difference between a positive and negative
vector is that the negative vector is directed
opposite the positive one. Thus for position relative to the X
at the front of the class room, a position to the left of the X
is a negative position and one to the right is a positive position.
A change of the position toward the left is a negative 
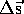. In the left-hand graph of velocity versus time shown above, the
change of velocity during any interval is negative and therefore the
acceleration is negative.
Return to Physics 125