 are examples
of the new kinds of energy that have been uncovered by this compelling
principle:
are examples
of the new kinds of energy that have been uncovered by this compelling
principle:
©Timothy E. Chupp, 1995
Our description of the principle of energy conservation requires us to search
for a ``new kind of energy'' whenever it appears that the law
is violated. Rotational energy, the neutrino and mc are examples
of the new kinds of energy that have been uncovered by this compelling
principle:
are examples
of the new kinds of energy that have been uncovered by this compelling
principle:
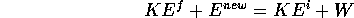
Let us now consider the process of doing work to lift a basketball to a height of 1m and letting it fall. Upon bouncing from a hard surface, energy conservation tells us that the ball can rebound to no higher than 2m, but in fact no basketball rebounds more than about 60% of its original height, or 1.2 m. For a 0.5 kg ball, this is a loss of translation kinetic energy (

mv

) of 4 J . Where does this 4 J go? The ball may pick up some spin as it bounces and thus rotational kinetic energy. The collision also produces sound which is the coherent motion of air molecules that jiggles your eardrums in perceptibly recognizable ways. Thus the increased kinetic energy of the air molecules helps account for the 4 J. But a careful accounting would show that there must be yet another kind of energy which would become more noticeable after repeating the process many times: the basketball warms up! That is, the basketball is heated. I would prefer to say that the quantity of heat of the basketball increases and that heat is a ``new kind of energy''. The change in the quantity of heat will be denoted

U. Thus
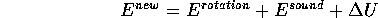
We will soon look more closely at the heat of an object as the total of translational and rotational kinetic energy of the microscopic constituents of the object. Thus the heat of the basketball is the total kinetic energy of the rubber and air molecules of the ball; the heat of the air in the room is the total kinetic energy of all the air molecules in the room (80% N

, 20% O

with CO

, H

O, Ar and other gases); the heat of a block of ice is the total kinetic energy of the molecules of H

O in the ice.
The heat of an object is related to its temperature. We can perform experiments to reveal this relationship, such as dropping a mass which does not bounce at all and makes no sound. Thus the kinetic energy just before it collides with the ground is totally converted into heat. By varying the mass, the material and the height the following relationship will emerge:
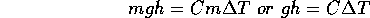
where h is the height from which the object of mass m is dropped,

T is the change in temperature of the object and C is a constant called the specific heat of the specific material. Specific heat is thus a measure of how much energy is needed to raise the temperature of a unit mass of a substance by a specified number of degrees (usually one degree C).
The specific heat depends on the material, the temperature and other factors such as the pressure exerted on the material. The following table gives the specific heats of a few materials:
Specific Heats of Selected Materials at Room Temperature and Atmospheric Pressure
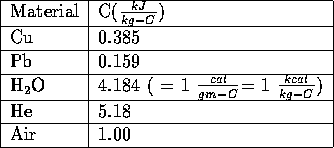
A kJ is a kilo-Joule which is 1000 Joules. The calorie (cal) is a unit that was invented so that the specific heat for water is 1

. The kcal (1000 cal) is sometimes written Calorie and is pronounced the same way. This is the unit known to everyone, especially those who count them.
If two objects with different temperatures are placed in thermal contact such that heat can flow from one to the other, they will both come to the same final temperature that is between the two initial temperatures. This is a remarkable phenomenon, but one that is very common: any hot object will eventually cool until its temperature is the same as its surroundings and the surroundings will warm up. This phenomenon can be understood by considering the following experiment:
Figure 1 Two objects, initially at different temperatures, come to an equilibrium temperature due to transfer of heat energy from the hotter to the colder.
Container 1 is at T , and container 2 is at T
, and container 2 is at T where T
where T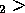 T
T .
Imagine a few atoms from 1 traded with the same number of atoms from 2.
Now since the temperature of 2 is higher, the trade will result in
a bit more heat added to 1 than was taken away and a bit more heat
taken away from 2 than was added. Thus the temperature of 2 will drop
a bit and the temperature of 1 will rise a bit. If we continue the trading
process, a point will be reached at which the temperature of 2 will
be lower than that of 1 and the next trade will result in 2 warming up a bit.
Then next trade will result in 1 warming and so on. When this condition
is reached, very nearly the same amount of heat is taken away from each as
is added to each, the temperature does not change, and the system has
reached thermal equilibrium (equal-balance).
.
Imagine a few atoms from 1 traded with the same number of atoms from 2.
Now since the temperature of 2 is higher, the trade will result in
a bit more heat added to 1 than was taken away and a bit more heat
taken away from 2 than was added. Thus the temperature of 2 will drop
a bit and the temperature of 1 will rise a bit. If we continue the trading
process, a point will be reached at which the temperature of 2 will
be lower than that of 1 and the next trade will result in 2 warming up a bit.
Then next trade will result in 1 warming and so on. When this condition
is reached, very nearly the same amount of heat is taken away from each as
is added to each, the temperature does not change, and the system has
reached thermal equilibrium (equal-balance).
In the case of gases, heat is actually transferred by the motion of
the molecules of the gas. This process is called convection. For
solid materials, it is not the atoms, but the atoms' energies that
are traded. To visualize this, imagine an atom moving with great speed
among many much slower atoms. With each, elastic collision, the fast atom
will loose some speed and its collision partner will gain some. The two
will move on to subsequent collisions until
the fast atom is no longer the fastest. This process of heat transfer is
called conduction.
A third important way to transfer heat is in the form of electromagnetic
energy which can carry energy. This is called radiative heat transfer
and is most convincingly demonstrated by use of the ``radiometer.''
Radiative energy transfer is that responsible for the cooling of the
surface of the earth on a clear night. The energy is transferred into space
which has the remarkably cold temperature of 270 C below zero!
C below zero!
We can make useful pictures or models of these processes with a few assumptions and derive predictions about the behavior of systems that are in fact verifiable. First, however, we'll introduce a new concept: entropy.
Entropy is a quantity like heat which we'll define in terms of its change as the result of a physical process: For a system at temperature T, the change in entropy is

where Q is the heat added to the system and T is the temperature in

K. Thus consider the situation described above, the establishment of thermal equilibrium. For container 1, a bit of heat (Q)is added at temperature T

and for container 2, a bit of heat is taken away (-Q) at temperature T

each time a few atoms are traded. Thus the changes of entropy are:
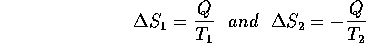
Since T

T

,

and therefore

. In the process of transferring heat from a warmer container to a cooler container (the natural flow of things) the quantity of entropy of the total system of two containers increases.
Consider another process: the cooling of water which forms ice. In order to form ice, liquid water at 0 C must loose heat, in fact 333 J for each gram. Thus the change of entropy of 1 gram of freezing water is -1.22

. In this case the change of entropy is negative and ice, the solid, crystalline form of water is formed.
The two processes for which we have found the change of entropy: the natural motion of heat from a warmer to cooler container and the freezing of water to form ice are both characterized by a change in the organization or order of the system. Two containers with different temperatures represent a more organized or ordered system than two containers whose temperatures are indistinguishable: more of the faster molecules are in container 2 at the start, but as the system moves toward thermal equilibrium, this organization disappears. Ice is a crystalline solid and more ordered than liquid water. In each case, the change toward a less ordered system is described by a positive change of the system's entropy. In this sense entropy is a measure of disorder, and the natural tendency of physical systems is toward disorder or increasing entropy. This tendency drives many physical processes and to overcome the tendency, energy has to be put into the system as we will soon see.
Processes which involve the movement of heat are called thermodynamic processes. Consider a container of fixed volume with an ideal gas inside. If we add heat to the gas, for example with a flame, and no change of state (i.e solid to liquid or liquid to vapor) the temperature must rise: the heat goes into the total kinetic energy of the molecules of the gas.
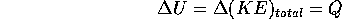
where U is the symbol used for (KE)

and Q is the heat added. This is just the principle of conservation of energy applied to the specific process described above.
Now let's put the piston back into action. If the temperature of the gas increases, the Ideal Gas Law tells us that either the pressure or volume or both must increase. If the gas in the container is allowed to expand and the weight of the plunger does not change, the pressure of the gas does not change and therefore the volume must increase.
For the case of constant pressure, the gas does work on the piston, W=

. The force is the pressure exerted by the gas multiplied by the surface area of the piston:

=

and the change of volume is

=

. Therefore
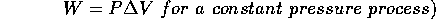
Conservation of energy requires that we must therefore also consider the work done by the gas:

Or in words: the change in the total energy of the gas is the heat added to the gas minus the work done by the gas.
It is useful to show the path of a thermodynamic process on a graph of P vs. V.
For the process of constant pressure expansion, the path is a horizontal line
and the area under the line (or curve) is P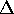 V, the work done by
the gas. In fact the work done by the gas is the area under the curve
on this graph regardless of the nature of the path. To convince yourself
that this is reasonable, break the process up into pieces for which the
pressure is roughly constant (an operation used several times before).
For a given number of moles of an ideal gas, each point on the P vs. V graph
also corresponds to a unique temperature T =
V, the work done by
the gas. In fact the work done by the gas is the area under the curve
on this graph regardless of the nature of the path. To convince yourself
that this is reasonable, break the process up into pieces for which the
pressure is roughly constant (an operation used several times before).
For a given number of moles of an ideal gas, each point on the P vs. V graph
also corresponds to a unique temperature T = 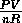 .
.
Two kinds of process are particularly useful: isothermal and adiabatic.
An isothermal process is one for which the temperature remains constant
and therefore
P=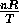
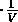 = const.
= const.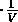 .
On the P vs. V. graph, this would be a hyperbolic curve resembling that
shown. Since the temperature is constant,
.
On the P vs. V. graph, this would be a hyperbolic curve resembling that
shown. Since the temperature is constant, 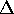 U = 0 and
U = 0 and
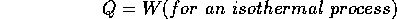
An adiabatic process is one for which no heat is added, i.e. Q= 0. The path of an adiabatic process on the P vs. V graph is shown, but it is not as straight-forward to predict it.
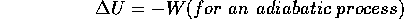
The utility of the isothermal and adiabatic processes arises from the fact (which we'll demonstrate below) that the change of entropy for the process is 0, that is, there is no change in the disorder of the system. Why is this so useful? Because a process for which the entropy does not change can be easily reversed. Consider the system shown below. A reservoir of heat at a constant temperature such as an ice bath at 0C transfers heat to a gas at the same, constant temperature. The work done by the gas is the area under the curve on the P vs. V graph, shown shaded in the figure drawn below. Conservation of energy for this isothermal process requires Q = W. The gas will do work on the piston. The change in entropy of the gas is

and the change in entropy of the reservoir is -

. Thus

S

= 0. Now let the piston do work on the gas until it returns to its initial pressure and volume. The path on the P vs. V graph is the same, only the arrow is reversed and the work done by the gas is of equal magnitude but it is negative as is Q. Again,

S

= 0. For an adiabatic process Q = 0 always and

S = 0 always.
In order to convince yourself that these reversible processes are indeed special, consider the isobaric (constant pressure) transition discussed earlier. As the gas expands with P constant, T =

V will increase. Since the gas is doing work W = P

V and U is increasing, heat must be added: Q =

U + W. This heat comes from a reservoir that must be at a higher temperature than the gas in order for heat to flow in the natural direction. Using the same principles as in the consideration of thermal equilibrium, the total change in entropy is positive. Is this process reversible, that is can the gas be returned to the initial pressure and temperature? In order to do this, work must be done on the gas and it will cool. But if it is still in contact with the reservoir at a higher temperature, heat will not naturally flow from cold to hot. We would need something like a refrigerator to transfer heat from the cooler gas to the warmer reservoir and electrical power for the refrigerator. Think about it: if we allow the gas to expand in a non-reversible way (

S

= 0) we will have to supply extra energy to return it to its initial state!
Truly isothermal or adiabatic process are very hard to realize experimentally. For a gas, the temperature is never completely uniform throughout and therefore even if the container is at a specified temperature, the entire volume of gas is probably not at that temperature. In fact, the only conditions under which a truly isothermal process can occur, i.e. true thermal equilibrium, is at one for which T = 0K. Adiabatic processes require perfect insulation which has not yet been developed, and would also require no molecular motion within the insulation, i.e. T = 0K.
The statements of the last two sections have been consolidated into the three laws of thermodynamics. They are
I. For a system,
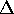 U = Q - W for any process. (This is, of course, just the law of
conservation of energy.)
U = Q - W for any process. (This is, of course, just the law of
conservation of energy.)
II. For any non-reversible process which takes a system from an initial state
(P , V
, V and T
and T ) to a final state (P
) to a final state (P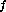 , V
, V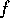 and T
and T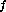 ),
additional energy must be added to return the system to the initial state.
Furthermore, a truly reversible process is possible only at T = 0K.
),
additional energy must be added to return the system to the initial state.
Furthermore, a truly reversible process is possible only at T = 0K.
III. There is a third law which I state with no further discussion because I cannot demonstrate or prove it. It is a form of pessimism: it is not possible to achieve T = 0.
A restatement of the laws might be:
I. You can't win.
II. You can't break even except at absolute zero.
III. You can't reach absolute zero.
Physics 125
This document was generated using the LaTeX2HTML translator Version 0.6.4 (Tues Aug 30 1994) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -link 0 -split 0 -no_navigation tsix.tex.
The translation was initiated by Scott D. Dexter on Tue Dec 5 16:35:32 EST 1995