© Timothy E. Chupp, 1995
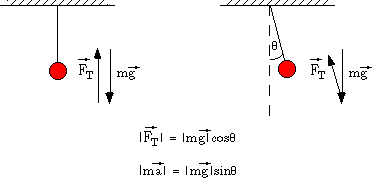
In our experience, any object at rest is nevertheless subject to a combination (or sum) of forces that balance. (Implicit in our considerations of "objects" up to now has been the simplifications that igonre the extent of the object, the exact position where the force is applied, and others that will be considered here.) This balance of forces is often true only at a special position of the object. Consider a our mass suspended from a cable, we'll call it Bob. The forces on Bob balance only when Bob is "at rest" and the cable is vertical. Only when the cable is vertical is the force of the cable on Bob exactly opposite the force of gravity on Bob. What happens when Bob is slightly displaced, so that the cable makes a small angle with the vertical? Well in order to maintain Bob at that displacement, an additional force must be applied to balance the forces. When the force is removed, there is an imbalance of forces on Bob, and it accelerates in a direction that will return it to the equilibrium position. However the momentum of Bob, when it reaches the equilibrium position, carries it past vertical to a slight displacement on the other side. It eventually reverses direction and the swings back etc. These are the oscillations of a pendulum about its equilibrium position. The equilibrium position is that where the forces on Bob are balanced.
In this example of Bob, the slight displacement from equilibrium leads to a force that pushes the object back toward its equilibrium position. (Note that the force is not directly toward the equilibrium position. See Figure 1.) This kind of equilibrium is called stable equilibrium because 1) the forces are balanced and 2) small displacements lead to restoring forces.

Figure 1: Bob suspended by a cable at its equilibrium position and displaced
by and angle 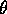 . The restoring forces push Bob toward the equilibrium
position which is stable.
. The restoring forces push Bob toward the equilibrium
position which is stable.
As another example, consider Bob supported by two pieces of wood connected at the appex of a triangle. It is in principle possible, if difficult, to "balance" Bob in this position. Once again the forces are balanced, however in this case a small displacement in either direction leads to a force that pushes Bob away from the equilbrium point. This is called unstable equilibrium.
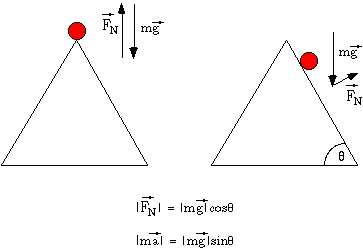
Figure 2: Bob supported by a triangle. The restoring forces push Bob away from the equilibrium position which is unstable.
These two examples both ignore the possibility that Bob can rotate without moving. To set Bob rotating without moving while at the end of the cable or at the apex of the triangle requires an additional pair of forces that are in opposite directions with equal magnitudes, BUT do not act along the same line. Such a pair of forces exerts a net torque, a vector quantity that will be defined below. For the case of Bob hanging from the cable, the nature of the cable resists the rotation and a restoring torque acts to rotate Bob toward the equilibrium rotational position.
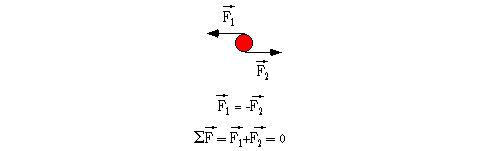
Figure 3: The forces 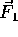 and
and 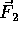 are balanced, and the forces of gravity
and the cable tension (into and out of the page) are also balanced. However, since
are balanced, and the forces of gravity
and the cable tension (into and out of the page) are also balanced. However, since
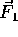 and
and 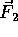 are not colinear, a net torque arises that can
rotate Bob away from the equilibrium rotational position.
are not colinear, a net torque arises that can
rotate Bob away from the equilibrium rotational position.
It is therefore most accurate to describe an object in equilibrium, not at rest. In equilibrium, the forces applied to the object are balanced and the torques applied to the object are balanced. For stable equilibrium, the restoring forces and/or torques always push the object toward the equilibrium position. For unstable equilibrium, the forces and/or torques push the object away from the equilibrium position.
A final example is an object that will be neither restored toward nor pushed away from an equilibrium position, such as a puck on an air table. This is sometimes called a position of neutral equilibrium because a displacement causes no change in the balance of forces and torques.
We will encounter many examples for which the forces balance, but are not colinear. Consider a see saw balancing two people of very different mass (for example Prof. Chupp (70 kg) and Theo (10 kg)). We'll be as accurate as possible here, so let's note that the see-saw itself has a mass of 20 kg, 10 kg on each side of the fulcrum. The figure shows how the forces on the see-saw balance: the masses push downward and the fulcrum pushes up.
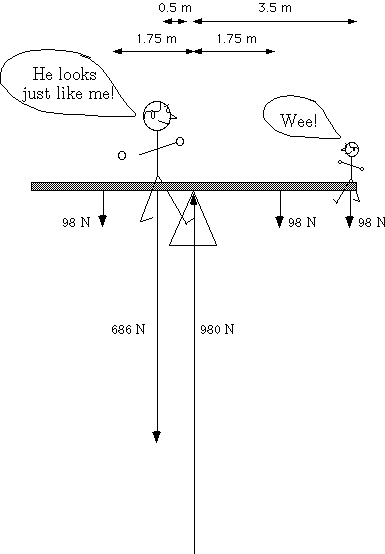
Figure 4: The forces on a seesaw due to 70 kg and 10 kg masses, the mass of the seesaw and the fulcrum.
You know well that Theo can balance me, but only if we are different distances from the
fulcrum. The reason is that the torque caused by the force of Theo must equal
the torque caused by me. Torque depends on both the force and the position
at which the torque is applied, called the position of the line of force. Both force and
torque are vectors. An imbalance of torques leads to a change of rotational motion around an axis
that is perpendicular to the force and to the displacement of the line of force from the
axis of rotation. Changes of rotational motion caused by torque will be
discussed more later. For now, we'll consider only cases for which the torques balance.
The torque about an axis caused by a force 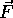 displaced from that axis by
displaced from that axis by
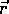 is
is

This is a new kind of vector equation that combines two vectors into a third vector
in three dimensions. Such a product of vectors is called the cross product.
The magnitude of the cross product of  and
and 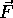 is
is

Where 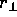 is the component of
is the component of 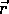 perpendicular to
perpendicular to 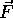 , that is
, that is
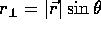 , where
, where 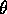 is the angle between
is the angle between 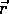 and
and 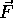 . So
. So

The direction of 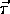 is along the axis around which the object would
rotate that is perpendicular to the plane containing
is along the axis around which the object would
rotate that is perpendicular to the plane containing 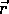 and
and 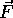 .
The rule is this: consider the direction the object at rest would begin to rotate
and curl the fingers of the right hand in that direction. The thumb points in
the direction of
.
The rule is this: consider the direction the object at rest would begin to rotate
and curl the fingers of the right hand in that direction. The thumb points in
the direction of 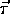 . This is called the right handed convention
or the right hand rule for defining the direction the result of a vector
cross product.
. This is called the right handed convention
or the right hand rule for defining the direction the result of a vector
cross product.
The seesaw with me and Theo is in equilbrium as long as the forces and torques balance. Here's how it works:
a.) 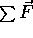 = 0
= 0
The forces are due to the force of gravity on each half of the seesaw (10 kg 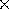 9.8 N/kg
each), the downward force of me on the left side (70 kg
9.8 N/kg
each), the downward force of me on the left side (70 kg 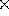 9.8 N/kg = 686 N), the downward
force of Theo (10 kg
9.8 N/kg = 686 N), the downward
force of Theo (10 kg 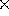 9.8 N/kg
and the upward force on the seesaw by the fulcrum (
9.8 N/kg
and the upward force on the seesaw by the fulcrum (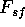 ):
):
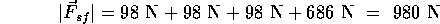
b.)  = 0
= 0
The torques are due to the force of gravity on each half of the see saw which
is directed at the center of mass of each half, and the torques due to
me and due to Theo. Note that the direction of the torque of the right
side of the seesaw and of Theo would rotate the seesaw clock-wise
and the torque due to me and the left hand side of the seesaw would rotate
the seesaw counter clock-wise. Thus the torques due to Theo (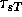 ) and me (
) and me (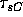 are
opposite (by the right hand convention:
are
opposite (by the right hand convention: 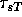 is into the page and
is into the page and 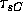 is out of the
page). The torques along an axis perpendicular to the page and passing through the
point of intersection of the seesaw and fulcrum balance as follows (notice that
is out of the
page). The torques along an axis perpendicular to the page and passing through the
point of intersection of the seesaw and fulcrum balance as follows (notice that  and
and 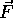 are perpendicular for each force so
are perpendicular for each force so 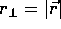 ):
):
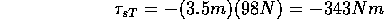
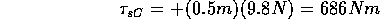
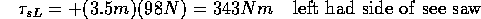
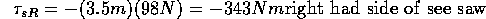
Everywhere you look, you will see objects in equilibrium. Hold your arm out. Sit, leaning back, in a chair. The awning of a cafe. Everywhere! Practice looking and analyzing the balance of forces and torques in things you see around you.
Return to Physics 125