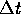is written
as
© Timothy E. Chupp, 1995
The velocity of an object
is its rate of change of position, which can be determined by measuring
its position at different times or by measuring the time it takes the object
to move a measured distance betweeen two points. This actually determines
only the average velocity during the interval, and is distinct from the
idealized notion of instantaneous velocity. The average velocity
during the interval 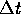is written
as
The arrow over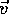 
reminds us that this quantity includes the
direction in which the object is moving. 
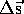is the
change in position which also includes the direction.
In order to observe such motion and thus determine the average velocity of an object over specified intervals, we can use a strobe light that provides flashes of light of very short duration (typically micro-seconds, i.e. 10^(-3) s or less) evenly spaced, say by 0.2 s. (The strobe rate is set to 300 flashes per minute.) The position of an air track cart (measured from a defined reference point) can be shown on a graph of position versus time. The velocity in any interval during the time considered is the same as in any other interval. This shows up as a straight line on the graph of position versus time, and is a special case of motion called uniform motion. Note that the definition of average velocity over an interval is identically the definition of the slope of the straight line on the position versus time graph, i.e.
The slope of a segment on the position versus time graph is the average velocity over the interval of time.
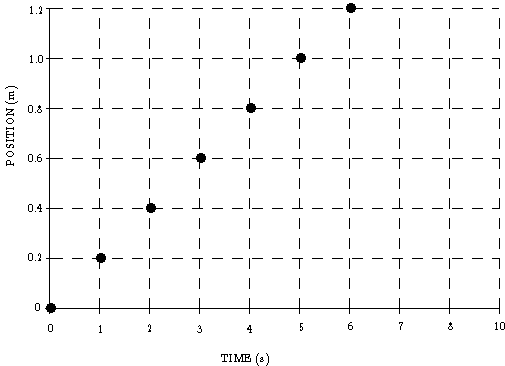
Figure 1: Positions of the air track cart at the times indicated. The average velocity is a constant 0.2 m/s from left to right.
It's easy to draw a graph of the velocity versus time, but this graph reveals something very important: The area under the curve of velocity versus time is the displacement over the given interval of time. This statement is accurate for non-constant as well as constant velocity, though it requires the Calculus introduced by Newton to prove it. For a constant velocity over an interval, the displacement is
And for our particular example of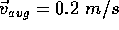 
from left to right, the displacement during a 6 second interval is
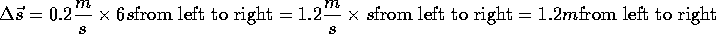
Note that the algebra of units, written out carefully, provides an answer for displacement in meters as it should. Always
be sure to check that the units of your answer make sense by careful dimensional analysis.
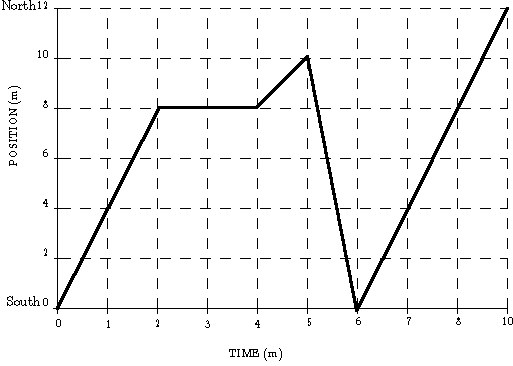
Figure 2: Theo's position along the wall, measured continuously as a function of time.
This graph shows the position of Theo, my 10 month old son, along a 12 meter long stone wall, running south to north, as time goes by. The horizontal axis represents the time measured from some starting time, say noon, and the vertical axis represents the position along some direction from a starting point, for instance the south end of the wall.
Consider the following questions about Theo's motion (which are typical of exam questions)
:
A. What was Theo's average velocity between 0 and 2 minutes?
B. between 2 and 4 minutes?
C. What was Theo's average velocity over the entire 10 minutes?
D. In which direction was Theo moving between 5 an 6 minutes?
E. Sketch a graph of Theo's velocity as a function of time.
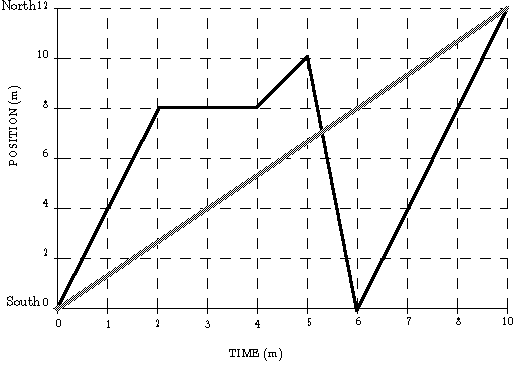
Figure 3: Theo's average velocity during the entire 10 minute interval is given by the slope of the line connecting his position at the beginning and at the end of the interval.
Theo's average velocity over the entire 10 minute interval is represented by the slope of line that connects his postion at the beginning and at the end of the interval.
Theo's velocity as a function of time is not constant since the slope of the lines on the position versus time graph change. However, there are four distinct intervals, each with a straight line representing Theo's position and therefore a uniform velocity over that interval, given by the slope of each line.
Finally, Theo's displacement, which can be determined from the graph of position versus time, can also be determined by the area under the curve on the velocity versus time graph. In the graph below, we can see how much distance Theo covered during each interval of uniform velocity.
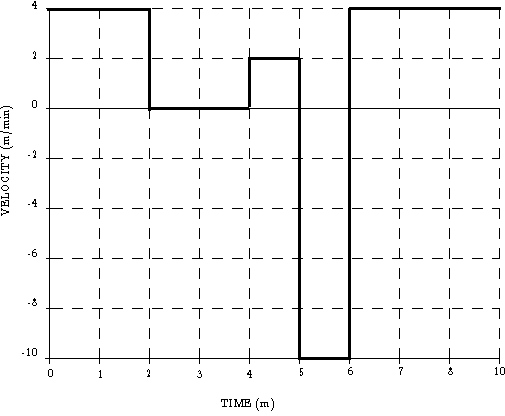
Figure 4: Theo's average velocity during each of the four intervals during which his velocity was constant is given by the slopes of each line.
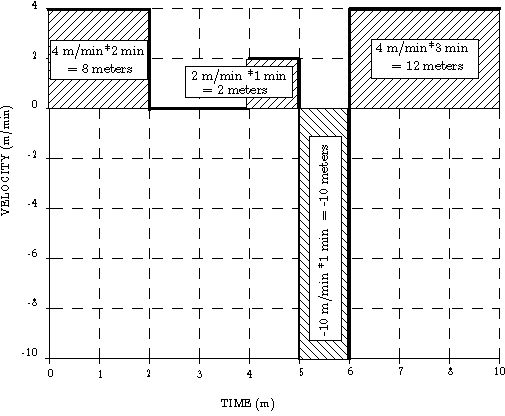
Figure 5: Theo's displacement for each of the four intervals is given by the area under the velocity versus time curve.
When the position of an object as a function of time is determined in a manner similar to that provided by the strobe light, only the average velocity during the intervals between flashes of the strobe can be determined, either as the slope on the position versus time graph or with the definition of average velocity over the interval. The fact that the strobe flash does last a finite (non-zero) length of time is not very significant, but to be exact, we might say that the instantaneous position of the object is revealed only as the duration of the strobe flash goes to zero seconds. Instantaneous velocity has a similar definition, as the limit of the average velocity over an interval as the duration of the interval goes to zero seconds. Such limits are the basis of the Derivatives of Calculus, and there is no need to manipulate them. The concept, however, is important.
Certain devices such as the radar and laser or LIDAR devices used by police measure velocity directly. This is done by the method of Doppler shifts, which detect the change in frequency (analagous to pitch for sound) of electromagnetic radio or light waves. The change in frequency is proportional to the velocity of the object from which the waves are reflected. Doppler radar can determine velocities measured over extremely short intervals and therefore provide a good approximation to instantaneous velocity. Thus we may also produce a graph of velocity versus time. How do we find the displacement over an interval? It is given by the area under the curve on the velocity versus time graph.
Return to Physics 125