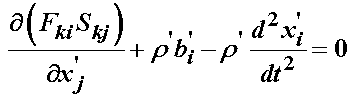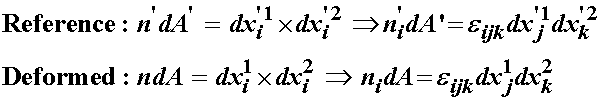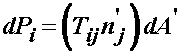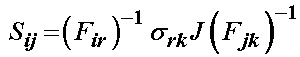BME 456: Biosolid Mechanics: Modeling and Applications
Section 4: Alternate Stress Tensors for Large Deformation
I. Overview
In Section 3 we introduced the concepts
of reference and deformed configurations, displacement, deformation gradient
tensor, and the small and large strain tensor. We noted that the small deformation
stress tensor was valid for the deformed configuration, just as the Cauchy
stress tensor developed in section 2. The large or finite strain tensor,
however, was developed using displacement gradients that refer to the reference
configuration. While the Cauchy stress tensor and the small strain tensor
are energetically conjugate, that is strain energy calculated as 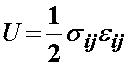 ,
is valid. At this point, we do not have a stress tensor that is energetically
conjugate to the finite strain tensor. Furthermore, we note that in section
2 we derived the stress equilibrium equation with respect to the Cauchy
stress tensor in the deformed configuration. The difficulty with this is
that we must know the deformed configuration to solve the stress equilibrium
equation. This leaves us with a chicken and egg problem in that to solve
the stress equilibrium problem we need to know the deformed configuration,
however, to know the deformed configuration we need to first solve the stress
equilibrium problem. Thus, to solve the nonlinear problems that arise out
of large deformation, we will need to refer all quantities back to the reference
configuration, including stress. Thus, the purpose of this chapter is to
define alternate stress tensors that we can refer to the reference configuration
and to define the stress equilibrium equation in the reference configuration.
The important concepts in this section to understand are:
,
is valid. At this point, we do not have a stress tensor that is energetically
conjugate to the finite strain tensor. Furthermore, we note that in section
2 we derived the stress equilibrium equation with respect to the Cauchy
stress tensor in the deformed configuration. The difficulty with this is
that we must know the deformed configuration to solve the stress equilibrium
equation. This leaves us with a chicken and egg problem in that to solve
the stress equilibrium problem we need to know the deformed configuration,
however, to know the deformed configuration we need to first solve the stress
equilibrium problem. Thus, to solve the nonlinear problems that arise out
of large deformation, we will need to refer all quantities back to the reference
configuration, including stress. Thus, the purpose of this chapter is to
define alternate stress tensors that we can refer to the reference configuration
and to define the stress equilibrium equation in the reference configuration.
The important concepts in this section to understand are:
1. Relationships between volume in reference and deformed configuration
2. Relationships between area in reference and deformed configuration
3. Definition of the First Piola-Kirchoff Stress
4. Definition of the Second Piola-Kircholff Stress
5. Definition of the Stress Equilibrium Equation in the reference configuration
II. Relationships between volume in the Reference and Deformed Configuration
The best and most straightforward place to start is to define the relationship between volume in the deformed and reference configuration. Recall from the section on mathematical preliminaries that we can calculate the volume in any space using three vectors, specifically as the cross product of two of these vectors dotted with the third. Let us consider three vectors in both the deformed and reference configuration:
Our goal is to convert the expression in terms of the deformed configuration to vectors in terms of the reference configuration. We know that an infinitesimal volume element may be written in the reference and deformed configuration as:
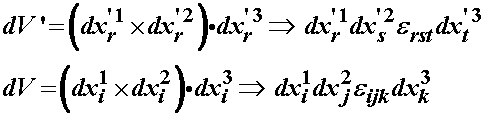
This can be done using the deformation gradient tensor:
![]()
Now, we can rewrite the above expression as:
![]()
While it is not readily clear, we can replace the quantity
![]()
with the following quantity:
![]()
as:
which gives us:
![]()
We may recall that the determinant of F is the third invariant of the deformation gradient tensor F. Also, we recognize that the last product of dx'1, dx'2, and dx'3 represents and infinitesimal volume element dV' in the reference configuration. Thus, we can rewrite the above as:
![]()
The above equations gives us the relationship between a volume dV in the deformed configuration and a volume dV' in the reference configuration. Many texts denote the determinant of F as the Jacobian, and denote the Jacobian as J. This would allow us to rewrite the above expression as:
![]()
If we divide the deformed configuration volume by the reference configuration volume, we see that the Jacobian J actually represents the ratio of the deformed configuration volume to the reference configuration volume:
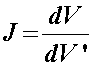
Likewise, if we want to know the reference volume in terms of the deformed volume, we can simply take the inverse of J since it is a scalar:
![]()
and then the inverse Jacobian represents the ratio of the reference configuration volume to the deformed configuration volume:
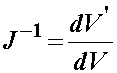
III. Relationships between area in the Reference and Deformed Configuration
Know that we have established the relationship between volumes in the reference and deformed configuration, we may now define relationships between surface area, since the volume ratio is used in the surface area relation. Again, we start with the calculation of the area as the cross product of two vectors. Without loss of generality, we consider two vectors on the surface of a body in both the reference and deformed configuration. These are denoted as:
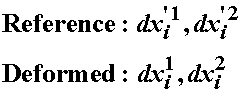
Before we take the cross product, note that the normal vector to the surface vectors in both configurations is can be computed as the cross product of two vectors divided by the magnitude of the cross product:
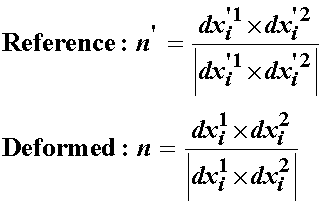
We also recall from the mathematical preliminary section that the area contained by the two vectors is simply the magnitude of the cross product. If we label the area in the reference configuraiton dA' and the area in the deformed configuration dA, the we can define these areas as:
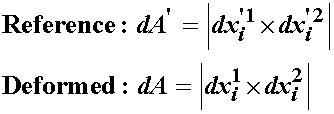
Therefore, if we multiply each normal vector by the surface area, we obtain the cross product itself as a result:
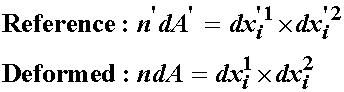
Now again, the trick becomes to write the reference configuration in terms of the deformed configuration. To do so, we will gain make use of the deformation gradient, only this time we will use its inverse. First, let's write the cross product in index notation:
We now use the deformation gradient tensor inverse and subsitute this into the normal-area definition in the reference coordinate system:
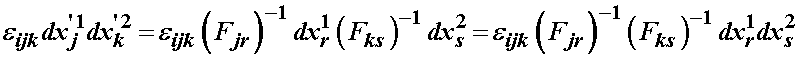
At this point we can now write:
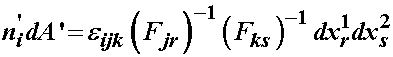
Now, to simply this expression, we multiply both sides by the quantity
![]() to
obtain:
to
obtain:
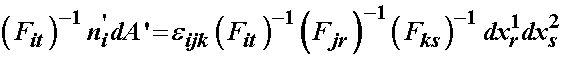
we that the terms on the right hand side except the dx terms are equivalent to the inverse Jacobian multipled by the permutation tensor. Thus, we can rewrite the above as:
![]()
or, multiplying both sides by J gives:
![]()
We recognize the right hand side of the above equation is actually the normal in the deformed configuration multiplied by the area in the deformed configuration. Thus, we can write:
This defines a relationship between normal vectors and areas in the reference configuration to normal vectors and areas in the deformed configuration. This is a fundamental formula in continuum mechanics known as Nanson's formula, and is used as a basis to develop alternate stress tensors.
IV. Derivation of Alternate Stress Tensors: Relationship to Cauchy Stress Tensor
Cauchy's stress tensor is defined in the deformed configuration and is thus not practical to use for large deformation analysis or experimental measures. Therefore, we need to develop alternative stress tensors. Two often used for large deformation mechanics are the 1st Piola-Kirchoff (PK) stress tensor and the 2nd Piola-Kirchoff (PK) stress tensor.
Let us consider first the 1st PK stress. The 1st PK stress is defined such that the total force resulting from the 1st PK stress multiplied by the normal and area in the reference configuration is the same as the total force resulting from the Cauchy stress times the normal and area in the deformed configuration. If we denote the total force over the infinitesimal area in both configurations as dP, the Cauchy stress as s, the infinitesimal deformed area as dA, we have:
![]()
recall that the stress times the normal is the traction force, which is defined per unit area. We can likewise generate the same total force in the reference configuration using the 1st PK stress T, the normal n' and the infinitesimal area dA' as:
The question becomes how the 1st PK stress is related to the Cauchy stress. To determine this, we need to write the normal and deformed area of the deformed configuration in terms of the normal and area of the reference configuration, which we will do using the Nanson formula derived in the previous segment. We know that we can equate the forces defined from stresses in two different configurations:
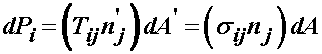
We can use Nanson's formula to define the normal times the area in the deformed configuration in terms of the normal times the area in the reference configuration:
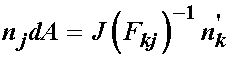
If we substitute the area expression into the total force expression, we have:

Note that in the above expression on the far right that j and k are both repeated dummy indices. Thus, it does not matter what letter we use for the index. Let's switch the j and k index in the above expression. This gives:
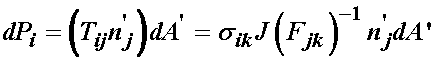
We next subtract the two right hand expressions from one another to give:
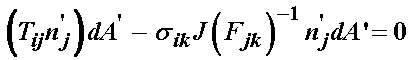
Since dA' is common to both expressions and a scalar, we can divide this term out. Since the normal n'j is common to both expressions, we can pull this term out and arrive at:
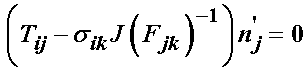
The expression in the brackets must hold for any arbitary normal vector, therefore we have the following relationship between the 1st PK stress tensor and the Cauchy stress tensor:
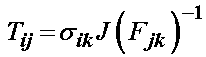
we can then also write the Cauchy stress tensor in terms of the 1st PK stress as:
![]()
Physical Interpretation: Since the 1st PK stress is defined in the reference configuration, it makes since that we multiply the Cauchy stress by the inverse of F to map back to the reference configuration. Also, if we divide through the original expression for the 1st PK stress by the reference area, then we get the following expression for the 1st PK stress traction:
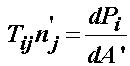
Physically, this indicates that the 1st PK stress is equivalent to dividing the total force in the deformed configuration by the area in the reference configuration. When testing soft tissues, this is the typical stress measurement that is made. We constantly monitor the force via the load cell in the testing system, hence the force in the current deformed configuration, but typically only make a measurement of the cross-sectional area in the reference configuration. Thus, any computed stress is the 1st PK stress.
One of the difficulties with the 1st PK stress is that it is not a symmetric stress tensor. We can see thus because we are multiplying a symmetric stress tensor, the Cauchy stress, with a generally non-symmetric deformation gradient tensor, we will have as a results a non-symmetric tensor. Such non-symmetry makes it difficult to form constitutive models. Therefore, the 2nd PK stress was developed to be a symmetric stress tensor for large deformation.
The 2nd PK stress involves one further mapping step between the reference and deformed configuration than the 1st PK stress. As such, it does not have such a straightforward physical interpretation as the 1st PK stress. To develop the total force dP is transformed from the deformed configuration to using the inverse of the deformation gradient tensor. If we call the transformed force dP', it may be written as:
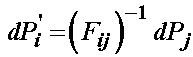
The 2nd PK stress Sij is defined such that the traction force resulting from the 2nd PK stress in the reference configuration multipled by the area in the reference configuration creates the transformed total force dP':
![]()
Taking the definition of the transformed total force as the inverse deformation gradient times the total force in the deformed configuration, we can write this in terms of the Cauchy stress tensor and area in the deformed configuration:
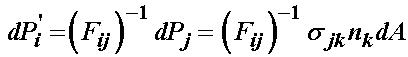
If we combine the representation of the total force using the 2nd PK stress and the Cauchy stress, we have:
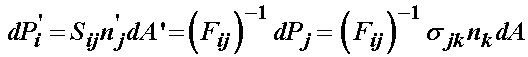
We can then directly write a relationship between the 2nd PK stress and the Cauchy stress:
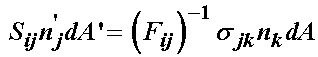
The question now of course is how to replace the deformed area and normal on the right hand side with the reference normal and area on the left hand side so we can make a direct represenation. To do this, we again utilize Nanson's formula to rewrite the deformed area normal product in terms of the reference area. Applying this in the above relation gives:
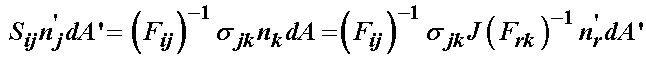
We need to write n'r in terms of the index j to combine the far left and far right terms in the above expression. To do this, we note that the indices j, k and r are all repeated in the far right expression and are thus dummy indices. As such, we may rearrange these indices without changing the meaning of the expression. In this case, if we switch the j and r indices we have:
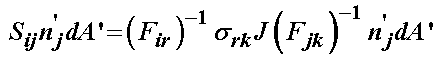
Combining these expressions we have:
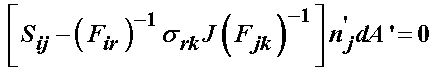
Since the expression inside the bracket must hold for any arbitrary normal and area, it must be equal to zero. Thus, we have the 2nd PK stress defined in terms of the Cauchy stress, inverse deformation gradient and Jacobian:
If instead we write the Cauchy stress in terms of the 2nd PK stress we have:
Now that we have both the 1st and 2nd PK stress defined in terms of the Cauchy stress tensor, we may write a relationsihip between the 1st and 2nd PK stress as:
![]()
we then can multiply both sides by J and by the inverse of Fjk to obtain the relationship between the 2nd PK and 1st PK stress::
V. Derivation of Stress Equilibrium in terms of the 1st and 2nd PK stress
We would now like to consider rewriting the stress equilibrium equation in the reference configuration. To do this, we are going to balance forces in an integral concept over the whole body. In other words, if we add up all the surface traction forces, the body forces and inertia forces on the body in the reference configuration, this amounts to integrating the surface forces over the area of the body, the body forces over the volume of hte body, and the inertia forces also over the volume of the body. We use the traction vector resulting from the 1st PK stress and the volume force and density also defined in the reference configuration. We write this integration of forces as:
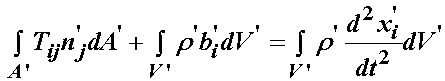
For the integral over the area, we need to apply the Gauss Divergence theorem. The Gauss divergence theorem states the following relationship between surface and volume integrals:
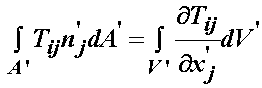
If we subsitute the result from the Gauss divergence theorem into the balance of forces we obtain:
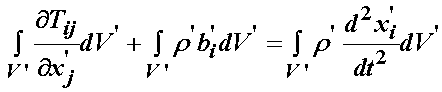
since all the terms are integrated over the reference volume, we may combine them under one volume integral:
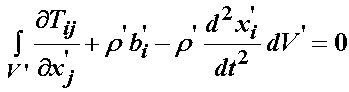
Thus, the terms inside the integral must equate to zero, giving us the stress equilibrium equation defined with respect to the reference coordinate system in terms of the 1st PK stress:
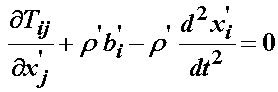
To derive the stress equilibrium equation in terms of the 2nd PK stress, we substitute for the 1st PK stress in the above equation using the relationship between the 1st and 2nd PK stress to obtain the stress equilibrium equation in the reference configuration in terms of the 2nd PK stress:
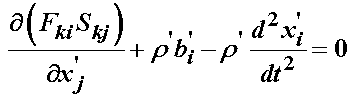
we compare the stress equilibrium equations written in terms of the 1st and 2nd PK stress to the stress equilibrium equation written in terms of the Cauchy stress for the deformed configuration:
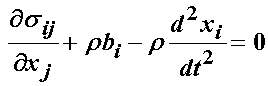
We can see that the stress equilibrium equation in the deformed configuration with the Cauchy stress tensor has the same form as the stress equilibrium with the 1st PK stress tensor in the reference configuration.
VI. Summary of Key Concepts
The purpose of this section was to define alternative stress tensors for large deformation analysis. As a basis, we first had to define relationships between area and volume in the reference and deformed configuration. Once these relationships were established, we could derive the 1st and 2nd Piola Kirchoff stress tensors in relation to the Cauchy stress tensor. Finally, we could rewrite the stress equilibrium equations using these alternate stress tensors in the reference configuration. This is very important for large deformation nonlinear analysis of soft tissues. In addition, these alternate stress tensors are important in the definition of hyperelastic consitutive equations for soft tissues. The key concepts and formula are repeated below:
Relationship between Volume in the Reference V' and the Deformed V Configuration:
![]()
Relationship between norma-Area product in the Reference A' and the Deformed A Configuration (Nanson's formula):
![]()
Definition of 1st Piola-Kirchoff Stress T in terms of Caucy Stress s:
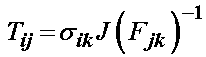
or in matrix form:
![]()
Definition of 2nd Piola-Kirchoff Stress S in terms of Caucy Stress s:
or in matrix format as:
![]()
We can then define the Cauchy stress in terms of the 2nd PK stress as:
![]()
or in matrix form as:
![]()
Relation of 1st Piola-Kirchoff Stress T to 2nd Piola-Kirchoff Stress S:
![]()
or in matrix form:
![]()
Definition of Stress Equilibrium Equation in Reference Configuraiton using 1st Piola-Kirchoff stress:
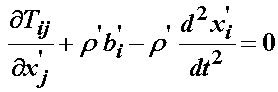
Definition of Stress Equilibrium Equation in Reference Configuraiton using 2nd Piola-Kirchoff stress: