Computer Assisted Concept Mapping and Analysis

Barbara Fife,

Northville Schools, Northville Michigan

Carl Berger

University of Michigan, Ann Arbor Michigan

National Association for Research in Science Teaching,

St. Louis. April 1996

Contact carl.berger@umich.edu

Objectives of the Study

The purpose of this study is to compare knowledge of experts and novices by computer analysis of concepts maps. The program is used to compare similarities between expert and novice concept maps, as well as to identify within novice maps common misconceptions or alternative conceptions, and missed relationships.

Significance of the Study

Traditional methods of producing and analyzing concept maps have relied upon pencil and paper generation of concept maps, frequently basing them on clinical interviews of students. The interview, hand drawing of the map, and hand scoring introduced by Novak (1984), are time consuming procedures that necessitate limiting the number of subjects and the statistical comparisons that are practicable in a given study.

Theoretical Underpinnings

Concept mapping was developed by Novak (1984) to depict learners’ conceptual change over time. This visualization clarifies how the learner links concepts within the domain of knowledge and reveals specific changes in knowledge constructs. Concept mapping has a place in the classroom teacher’s repertoire as an alternative assessment method. Typical multiple choice tests focus on rote learning and simple relationships, but cannot convey a more global understanding of the topic, while language and writing difficulties may mask accurately perceived relationships in student essay responses. Concept mapping provides a simple and direct way to show how students link ideas. Missing conceptions and alternative conceptions are easily recognized within concept maps, and the teacher can design further instruction accordingly.

Computer-based analysis of knowledge has been devised, notably by Schvaneveldt (1990) and Fisher (1990). Schvaneveldt uses Pathfinder analysis and has devised a program that produces a non-hierarchical linked spatial model. An intriguing feature of Pathfinder's program is the ability to constrain the data so that links disappear, showing which are the strongest and weakest cognitive links, based on the closeness rating. The concept maps generated by Pathfinder can be compared and analyzed statistically.

SemNet, developed by Kathleen Fisher and colleagues, is a fully developed computer tool for the construction of concept maps. A top down spatial orientation of the concepts does not necessarily show hierarchy. The sprawling nature of an "all inclusive" map makes it challenging to assess.

As an alternative to free mapping of concepts, students could be asked to map a set of concepts provided. Then, if knowledge maps could be consistent if not identical, the concept maps could be grouped, or clusters of student maps averaged, for comparison with other student groups or with an expert’s map.

Design and Procedures

The instructor provides a list of concepts and links, and students move and join concepts with links through the use of the computer program. The computer exports a coded listing of all relations found within each completed concept map. A matrix of concepts and links is generated for each concept map. The matrix representation of the relations within a given concept map makes possible numerous computer-based comparisons of concept map characteristics.

The following methodology identifies similarities in the concept maps.

1. Are the same concepts connected in both maps? Whether or not the same linking propositions are used and whether or not the directionality of the linkage is the same, do both maps indicate a relationship between the same concepts?

2. Between the concepts, are the same linking propositions used? Whether or not the directionality of the linkage is the same, do both maps use the same linking proposition for the relation between the two matching concepts?

3. For each pair of matching concepts with matching linking propositions, is the directionality of the relation the same in both maps?

These questions, answered in this order of priority, layer the similarity between the two maps. The first question evaluates the skeleton of the concept maps, asking only whether the concepts are connected to one another in the same way. The second question focuses on the agreement of the linking proposition used to define the relationship between each matching pair of concepts. The third question answers to what degree the concepts, links and directionality of relations match. The third question, then, provides the most rigorous appraisal of the congruence between the maps, while the first and second questions allow for differences in linking propositions and/or directionality of the relation. One criteria of a successful algorithm for the comparison of two concept maps is that it yields the same results as a visual inspection of the maps being compared.

Several measures of comparison of concept maps have been developed in the computer program. Based on the work of Goldsmith and Acton (1989), the C-measure algorithm, the following new measures of similarity were developed for the project. Taken together, the comparisons provide a measure of the global similarity or congruence between any two concept maps. In the A-measure the program looks to see if the same concepts are connected by any link in any direction. Thus the following simple comparisons would show an A-measure of 1.0

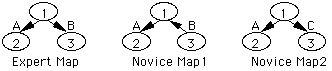
Figure 1. Example expert and novice maps showing concepts as numbers, links as letters and arrows for direction of links.

Table 1

Relationships between Expert and Novice 1 and Novice 2 Concept Maps

Type of measure	Expert to Novice 1	Expert to Novice 2
A-Measure	1.00	1.00
B-Measure	1.00	0.50
F-Measure	0.33	0.50
Average	0.71	0.67

The B-measure compares the choice of linking proposition, but without regard for the directionality of the link between the two matching concepts. The F-measure or full-measure assesses total congruence between the maps including concepts, linking propositions, and directionality of the relations. In addition to these similarity measures, a difference or D-measure was created to identify within novice concept maps common alternative relations and missed concepts.

Other comparisons are possible: the computer program may be used to identify the relatedness or connectedness of each concept, levels of hierarchy, branching, cross-linking, and inter-concept distances. Finally, a map score representing the complexity of the concept map can be derived from these characteristics.

Findings

It is possible to discriminate for large numbers of students as well as pairs of students on concept maps. It is possible to identify common misconceptions in alternative links and link directions. As important is the ease to which missed concepts are highlighted and presented in clear graphical patterns. Further research needs to be done to determine whether the identification of common misconceptions and missing conceptions can ameliorate actual classroom instruction, which is beyond the scope of this paper.

Conclusion

To use concept mapping more effectively as a means of assessing student understanding, more powerful tools are needed to see how students identify relationships. Tools are needed which not only make it easier for the teacher, but also provide insights that laborious hand analysis would prevent. This paper has demonstrated the possibility of using a computer program as well as the constraints in using a computer program, and has provided insights to how such measures can identify common misconceptions that need further class time, or identify groups of students having alternative perceptions so that group or individual support can be provided, thus improving learning for all students.

Bibliography

Fisher, Kathleen M. (1990). Semantic Networking: The New Kid on the Block. Journal of Research in Science Teaching, 27(10), 1001—1018.

Fisher, Kathleen M. (1994). Which Text Mapping System is Best? Mapping Book Chapters with SemNet: Example Views. Symposium Proceedings of the 1994 Annual Meeting of the American Educational Research Association, New Orleans, LA.

Goldsmith, T.E., Johnson, P.J. & Acton, W.H. (1991). Assessing structural Knowledge. Journal of Educational Psychology, 83, 88—96.

Groulx, Judith & Dansereau, Donald F. (1994). Knowledge Maps: Some How-To’s for Interpretation and Construction. Symposium Proceedings of the 1994 Annual Meeting of the American Educational Research Association, New Orleans, LA.

Jonassen, D. H., Beissner, K. & Yacci, M. (1993). Structural Knowledge: Techniques for Representing, Conveying, and Acquiring Structural Knowledge. Hillsdale, NJ: Erlbaum.

Malone, John & Dekkers, John. (1984). The Concept Map as an Aid to Instruction in Science and Mathematics. School Science and Mathematics, 84(3):220—232.

Markham, Kimberly M., Mintzes, Joel J. & Jones, M. Gail. (1994), The Concept Map as a Research and Evaluation Tool: Further Evidence of Validity. Journal of Research in Science Teaching, 31(1):91—101.

Miller, Bill, Faletti, Joseph & Fisher, Kathleen M. (1991). SemNet User’s Guide. SanDiego, CA:SemNet Research Group

Moreira, Marco A.. (1987). Concept Mapping as a Possible Strategy to Detect and to Deal with Misconceptions in Physics. Proceedings of the Second International Seminar on Misconceptions and Educational Strategies on Science and Mathematics. Ithaca, NY: Cornell University.

Novak, Joseph D. (1977). A Theory of Education. Ithaca, NY: Cornell University Press.

Novak, Joseph D. (1984). Application of Advances in Learning Theory and Philosophy of Science to the Improvement of Chemistry Teaching. Journal of Chemical Education, 61(7), 607—612.

Novak, Joseph D. (1990). Concept Mapping: a Useful Tool for Science Education. Journal of Research in Science Teaching, 27(10), 937—949.

Novak, Joseph D. (1993). Human Constructivism: A Unification of Psychological and Epistemological Phenomena in Meaning Making. International Journal of Personal Construct Psychology, 6(2), 167—193.

Novak, Joseph D. & Gowin, D. B. (1984). Learning How to Learn. Cambridge, England: Cambridge University Press.

Novak, Joseph D. & Musonda, Dismas. (1991). A Twelve Year Longitudinal Study of Student Science Concept Learning. American Educational Research Journal, 28(1), 117—153.

Novak, Joseph D. & Wandersee, James H. (1994). Using Concept Maps to Help Students Learn How to Learn. Symposium Proceedings of the 1994 Annual Meeting of the American Educational Research Association, New Orleans, LA.

Pendley, Bradford D., Bretz, Richard L. & Novak, Joseph D. (1994). Concept Maps as a Tool To Assess Learning in Chemistry. Journal of Chemical Education, 71(1), 9—15.

Schvanevelt, Roger W., Ed. (1990). Pathfinder Associative Networks: Studies in Knowledge Organization. Norwood, NJ:Ablex.

Wallace, Josephine. D. & Mintzes, Joel J. (1990). The Concept Map as a Research Tool: Exploring Conceptual Change in Biology. Journal of Research in Science Teaching, 27(10), 1033—1052.

Wandersee, James H. (1990). Concept Mapping and the Cartography of Cognition. Journal of Research in Science Teaching, 27(10), 923—936.

White, Richard. and Gunstone, Richard. (1992). Probing Understanding. New York: The Falmer Press.