Adaptive Mesh
Refinement (AMR) techniques provide an attractive framework for
atmospheric flows since they allow an improved resolution in limited
regions without requiring a fine grid resolution throughout the entire
model domain. The model regions at high resolution are kept at a
minimum and can be individually tailored towards the research problem
associated with atmospheric model simulations.
A solution-adaptive grid is a virtual necessity for resolving a problem
with different length scales. In order to avoid under-resolving
high-gradient regions in the problem, or conversely, over-resolving
low-gradient regions at the expense of more critical regions, solution
adaptation is a powerful tool saving several orders of magnitude in
computing resources for many problems. Climate and weather models, or
generally speaking computational fluid dynamics (CFD) codes, are among
the many applications that are characterized by multiscale
phenomena and their resulting interactions.
For instance, large-scale weather systems such as midlatitude cyclones
drive small-scale frontal zones, thunderstorms or rain events. These
small-scale features may then influence the larger scale if, as an
example, evaporation processes and turbulence at the surface trigger
sensible and latent heat fluxes. But although today's atmospheric
general circulation models (GCMs), and in particular weather prediction
codes, are already capable of uniformly resolving horizontal scales of
order 10-20 km (e.g. the model IFS of the European Centre for
Medium-Range Weather Forecasts), the atmospheric motions of interest
span many more scales than those captured in a fixed resolution model
run. The widely varying spatial and temporal scales, in addition to the
nonlinearity of the dynamical system, raise an interesting and
challenging modeling problem. Solving such a problem more efficiently
and accurately requires variable resolution.
The adaptive FV dynamical core has been
run in two configurations: the full 3D hydrostatic dynamical core on
the sphere and the corresponding 2D shallow water model that has been
extracted out of the 3D version (
Jablonowski 2004,
Jablonowski et al. 2004,
Jablonowski et al. 2006,
St-Cyr et al. 2008,
Jablonowski et al. 2009). In general, the shallow water system
can be considered a 1-level version of the 3D dynamical core. This
shallow water setup serves as an
ideal testbed for the horizontal discretization and the 2D
adaptive-mesh strategy. It further allows the efficient and quick
testing of
interpolation routines at fine-coarse grid interfaces.
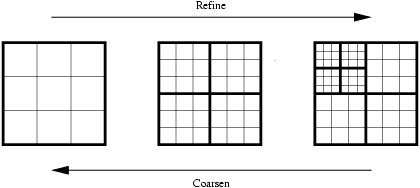
Both static and dynamic adaptation strategies have been tested. Static
adaptations can be used to vary the resolution in pre-defined regions
of interest. This includes static refinements near mountain ranges or
static coarsenings in the longitudinal direction for the implementation
of a so-called reduced grid in polar regions. Dynamic adaptations are
based on flow characteristics and guided by refinement criteria that
detect user-defined features of interest during a simulation. In
particular, flow-based refinement criteria, such as vorticity or
gradient indicators, have been tested. Refinements and coarsenings then
occur according to pre-defined threshold values.
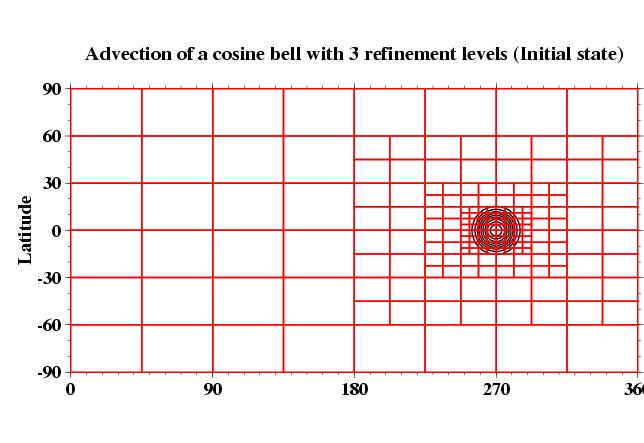
An example of an adaptive passive advection test on the sphere is shown
below. The figure shows the initial conditions for the shallow water
standard test case 1 with a 90
o rotation angle (see
Williamson et a. 1992 for the test
specifications). Here the adapted blocks track a cosine bell as it is
transported once around the sphere. Note that each self-similar blocks
contains 9x6 grid points in lon x lat direction so that the finest grid
resolution in this example corresponds to a 0.625
o x 0.625
o
grid. The maximum number of refinement levels is set to 3.
The adaptation criterion is based on a simple threshold assessment. A
block is refined as soon as the height of the cosine bell exceeds a
user-determined threshold value at (at least) one grid point within the
block. On the other hand, a block gets coarsened if the height of the
cosine bell in the block no longer meets the criterion. The
corresponding
mpeg movie (4.1 MB)
shows that the cosine bell is successfully captured as indicated by the
overlaid block distribution. The movie shows a 12-day simulation. After 12-days
the tracer distribution returns to its initial position which then serves
as the reference solution. There are no visible distortions of the
height field as the cosine bell approaches, passes over and leaves the
poles. The increased resolution clearly helps preserve the shape and
peak amplitude.
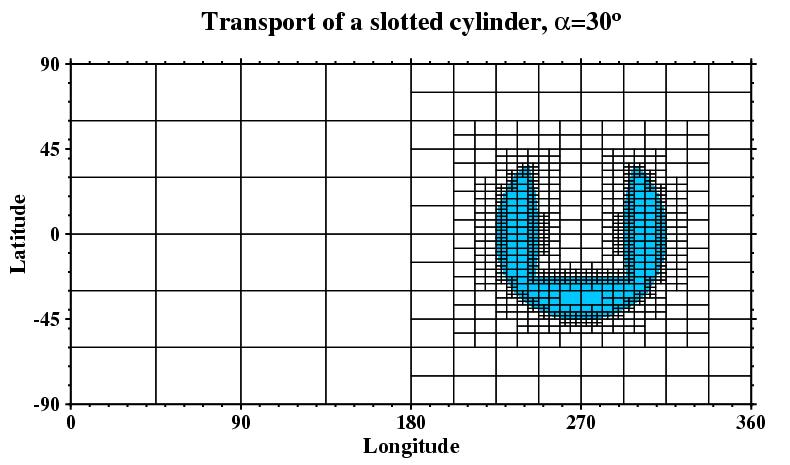
The cosine bell represents a rather smooth tracer
distribution. An alternative tracer field is shown below and also in this 12-day
simulation (4.4 MB)
with a rotation angle of 30
o.
The slotted cylinder is initialized with a constant value and is set to zero outside the inner domain. The movie shows that the sharp edges are tracked successfully by a gradient-based refinement criterion.
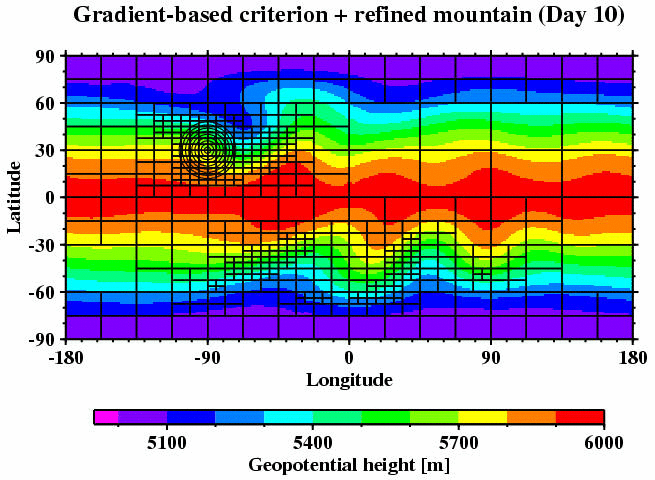
An example of a dynamically adapted nonlinear flow field is presented in
the next figure. It shows an idealized flow over a single mountain at
model day 10 (test case 5,
Williamson
et a. 1992). Here the adaptations are guided by the absolute value
of the geopotential height gradient. The refined regions pick out the
strong gradient regimes that are associated with the evolving wave
train behind the mountain. Other refinement criteria are also feasible for this mountain-induced wave response.
For example, the following
15-day
mpeg movie (5 MB)
shows the evolution of the geopotential height field that is dynamically
tracked by a relative vorticity refinement criterion.
It detects the evolving lee-side wave reliably and highlights slightly different
refinement regions in comparison to the gradient criterion shown below.
Carpenter,
R. L., K. K. Droegemeier, P. R. Woodward and C. E. Hane, Application
of the Piecewise Parabolic Method to Meteorological Modeling, Mon. Wea.
Rev., 118, 586-612, 1990.
Colella, P. and P. R. Woodward, The Piecewise
Parabolic Method (PPM) for Gas-Dynamical Simulations, J. Comput. Phys.,
54, 174-201, 1984.
Ferguson, J. O., C. Jablonowski, H. Johansen, P. McCorquodale, P. Colella and P. A. Ullrich,
Analyzing the Adaptive Mesh Refinement (AMR) characteristics of a high-order cubed-sphere 2D shallow water model,
Mon. Wea. Rev., 144, 4641-4666, 2016
Ferguson, J. O., C. Jablonowski, and H. Johansen,
Assessing Adaptive Mesh Refinement (AMR) in a Forced Shallow-Water Model with Moisture,
Mon. Wea. Rev., Vol. 147, 3673–3692, 2019
Jablonowski, C., Adaptive Grids in Weather and Climate
Modeling, Ph.D. dissertation, University of Michigan, Ann Arbor, MI, 2004
(
download the pdf version,
8MB),
Jablonowski, C., M. Herzog, J. E. Penner,
R. C. Oehmke, Q. F. Stout and B. van Leer, Adaptive Grids for Weather and Climate Models,
ECMWF Seminar Proceedings on Recent Developments in Numerical
Methods for Atmospheric and Ocean Modelling, Reading, UK, 6-10
September 2004, pp. 233-250 (download the
pdf version 2MB)
Jablonowski, C., M. Herzog, J. E. Penner,
R. C. Oehmke, Q. F. Stout, B. van Leer and K. G. Powell, Block-Structured Adaptive Grids
on the Sphere: Advection Experiments, Mon. Wea. Rev., 134, 3691-3713, 2006
Jablonowski, C. and D. L. Williamson, A
Baroclinic Instability Test Case for Atmospheric Model Dynamical Cores,
Quarterly J. Roy. Met. Soc., 132, No. 621C, 2943-2975, 2006
Jablonowski, C., R. C. Oehmke and Q. F. Stout,
Block-structured Adaptive Meshes and Reduced Grids for Atmospheric General Circulation Models,
Phil. Transaction Royal Society A, 367, 4497-4522, 2009
Lin, S.-J., A Finite-Volume Integration Method for
Computing the Pressure Forces in General Vertical Coordinates, Quart.
J. Roy. Meteor. Soc., 123, 1749-1762, 1997.
Lin, S.-J., A "Vertically Lagrangian"
Finite-Volume Dynamical Core for Global Models, Mon. Wea. Rev., 132,
2293-2307, 2004.
Lin, S.-J. and R. B. Rood, Multidimensional
Flux-Form Semi-Lagrangian Scheme, Mon. Wea. Rev., 124, 2046-2070, 1996.
Lin, S.-J. and R. B. Rood, An Explicit
Flux-Form Semi-Lagrangian Shallow Water Model on the Sphere, Quart. J.
Roy. Meteor. Soc., 123, 2477-22498, 1997.
McCorquodale, P., P. A. Ullrich, H. Johansen, and P. Colella, An adaptive multiblock high-order finite-volume method for solving the shallow-water equations on the sphere. Communications in Applied Mathematics and Computational Science, 10 (2), 121–162, 2015.
Oehmke, R. C. and Q. F. Stout, Parallel
Adaptive Blocks on a Sphere, in
Proc. 11th SIAM Conference on Parallel Processing for Scientific
Computing, 2001, CD-ROM.
Oehmke, R. C., High Performance Dynamic Array
Structures, Ph.D. Dissertation, University of Michigan, Ann Arbor,
2004, Department of Electrical Engineering and Computer Science, 93 pp.
St-Cyr, A., C. Jablonowski, J. M. Dennis, H. M. Tufo and S. J. Thomas, A Comparison of Two Shallow Water Models with Non-Conforming Adaptive Grids,
Mon. Wea. Rev., 136, 1898-1922, 2008.
van Leer, B., Towards the Ultimate
Conservative Difference Scheme. II. Monotonicity and Conservation
Combined in a Second-Order Scheme, J. Comput. Phys., 14, 361-370, 1974.
van Leer, B., Towards the Ultimate
Conservative Difference Scheme. IV. A New Approach to Numerical
Convection, J. Comput. Phys., 23, 276-299, 1977.
Williamson, D. L., J. B. Drake, J. J. Hack,
R. Jakob and P. N. Swarztrauber, A Standard Test Set for Numerical
Approximations to the Shallow Water Equations in Spherical Geometry, J.
Comput. Phys., 102, 211-224, 1992