If we assume ideal gas behavior, then calculating the moles of A initially present in the reactor is quite simple. We insert our variables into the ideal gas equation:
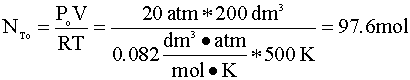
Knowing the mole fraction of A (yAo) is 75%, we multiply the total number of moles (NTo) by the yA:
![]()
The initial concentration of A (CAo) is just the moles of A divided by the volume:
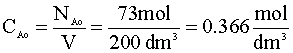
With both 1st and 2nd order reactions, we will begin with the mole balance:
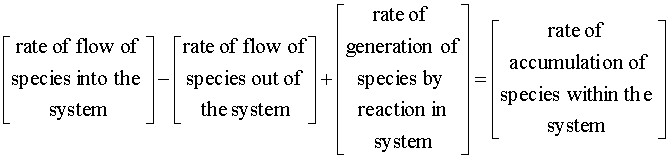
![]()
There is no flow in or out of our system, and we will assume that there is no spatial variation in the reaction rate. We are left with:
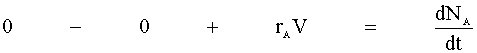
Knowing the moles per volume (NA/V) is concentration (CA), we then define the reaction rate as a function of concentration:
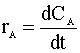
First Order Reaction
This is the point where the solutions for the different reaction orders diverge.
Our first order rate law is:
![]()
We insert this relation into our mole balance:
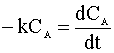
and integrate:
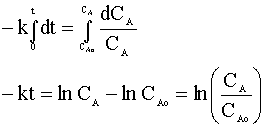
Knowing CA=0.01 CAo and our rate constant (k=0.1 min-1), we can solve for the time of the reaction:
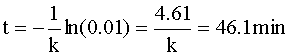
Second Order Reaction
Our second order rate law is:
![]()
We insert this relation into our mole balance:
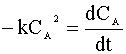
and integrate:
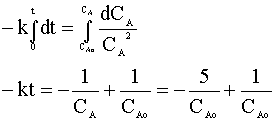
We can solve for the time in terms of our rate constant (k = 0.7) and our initial concentration (CAo):
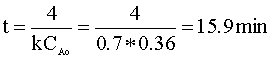
To determine the pressure of the reactor following this reaction, we will again use the ideal gas law. First, we determine the number of moles in the reactor:
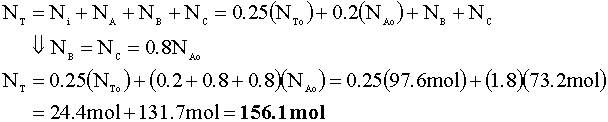
Now, we calculate the new pressure using the ideal gas law:
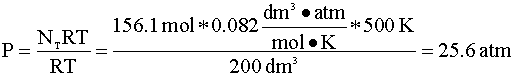
Back to problem statement.