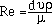
To aid in the effective design of impellers, several dimensionless numbers have been introduced. The first of the dimensionless numbers we will define is the impeller Reynold's number, NRe, which is used to characterize the flow in the tank as either laminar, turbulent, or in the transition region. The impeller Reynold's number can be derived from the Reynold's number for flow in pipes, Re.

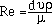
where:

d is the inside diameter of the pipe

u is the fluid velocity

r is the fluid density

m is the fluid viscosity

The impeller Reynold's number can be obtained by substituing in the impeller diameter, D, for the pipe diameter and the angular velocity of the impeller, ND, for the fluid velocity to yield:

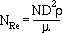
where:

N is the rotational speed of the impeller

D is the impeller diameter

Another dimensionless quantity commonly used to characterize impellers is the power number, NP. It has been shown through experimental data that the power consumption of an impeller, P, is proportional to the cube of the rotational speed of the impeller, the fifth power of the impeller diameter, and the density of the fluid. Therefore, the following relationship holds :

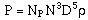
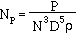
Two other dimensionless numbers that are encountered are the Froude number, N_Fr, and the pumping number, N_q. The Froude number is defined as

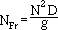
where: g is gravitational acceleration

The Froude number is useful in studying vortex motion during scale up. The pumping number is defined as:

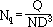
and can be used to find the pumping rate of the impeller, Q.

To the Mixing in Chemical Reactors Main Page