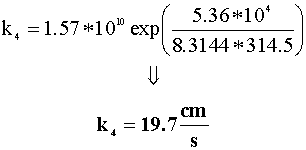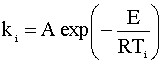
For this problem, the behavior of the beetle can be modeled by the Arrhenius equation. Essentially, the beetle's speed (k) increases exponentially with increases in temperature.
We begin with the Arrhenius equation:
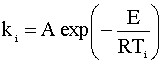
In order to calculate how fast the beetle can push the ball, we will need to determine the activation energy (E) and the Arrhenius coefficient (A) of the beetle.
We will arrange our data as such:
|
Rate Constant (cm/s) |
Temperature (K) |
|
k1 = 6.5 |
T1 = 300 K |
|
k2 = 13 |
T2 = 310 K |
|
k3 = 18 |
T3 = 313 K |
|
k4 = ? |
T4 = 314.5 K |
To solve the problem graphically and get an approximate answer, we may plot ln(k) vs. 1/T. This plot should form a straight line and will predict the ln(k) for T=314.5 K.
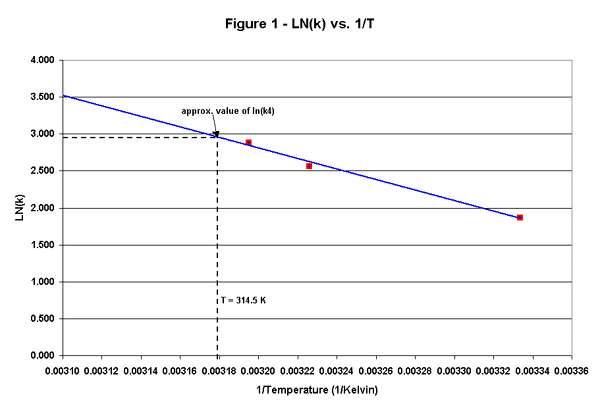
As we can see here, ln(k) for T=314.5 is equal to ~2.95. This corresponds to a k4 value of 19.1 cm/s.
Now we will solve the problem numerically to get an exact answer. By dividing k1 by k2 we can eliminate A and solve for E:
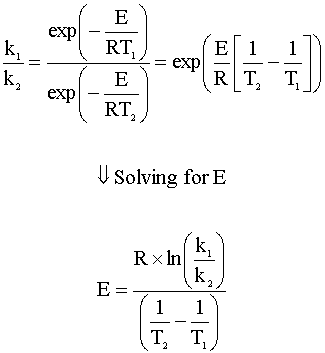
Then inserting the values for our variables (k1, k2, T1, T2), we get
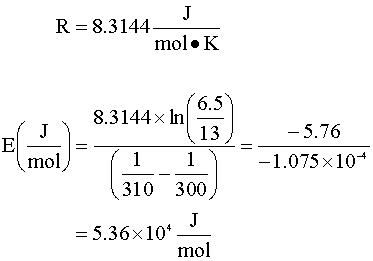
Inserting this activation energy into our Arrhenius equation for k3, we can solve for our coefficient (A):
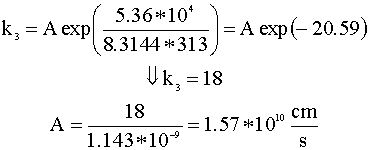
Now that we have solved for our Arrhenius constants, we can calculate the rate (k4) at which the beetle pushes the ball at 314.5 K: