The first step in setting up our stoichiometric table is to determine the stoichiometric coefficients (a, b, c, d, & e).
![]()
After making sure the elements are balanced on both sides of the above equation, the complete equation looks like:
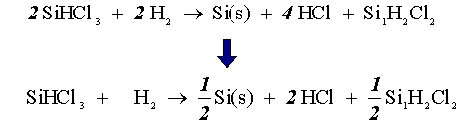
We will assume that our reactor acts like a PFR in setting up our stoichiometric table.
The stoichiometric table consists of the species name (I), species symbol (II), the flow rate in (III), the change in flow rate (IV), and the flow rate out (V). We will demonstrate how the table is set up with an example on the trichlorosilane (SiHCl3).
Our first species is trichlorosilane (SiHCl3).
We will give SiHCl3 the symbol A.
The flow of A into the PFR is FAo.
The change in flow of A will be -FAoX. Where X is conversion.
The flow of A out of the system is FAo(1-X).
The complete stoichiometric table is given below:
|
Species |
Symbol |
Flow Rate In |
Change in Flow Rate |
Flow Rate Out |
|
SiHCl3 |
A |
FAo |
-FAoX |
FAo(1-X) |
|
H2 |
B |
FAo |
-FAoX |
FAo(1-X) |
|
Si |
C |
0 |
0.5FAoX |
0.5FAoX |
|
HCl |
D |
0 |
2FAoX |
2FAoX |
|
Si1H2Cl2 |
E |
0 |
0.5FAoX |
0.5FAoX |
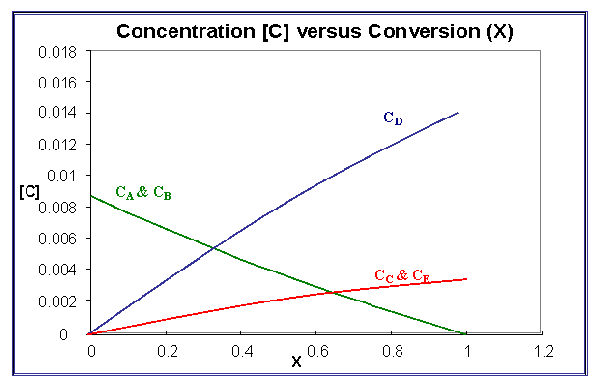
The second part of the problem is to sketch the concentration of each species as a function of conversion.
If the PFR operates at constant temperature (T) and pressure (P) then we know the total concentration (CT) by the following relation:

Under constant temperature and pressure, the concentration of each species (Ci) is:
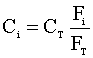
Knowing that CTo = CT.
The total molar flow rate (FT) is:
![]()
Where d is:
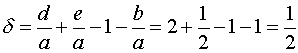
We do not include component C in this calculation because it is a solid.
Combining the above equations, the concentration of each species can be written as:
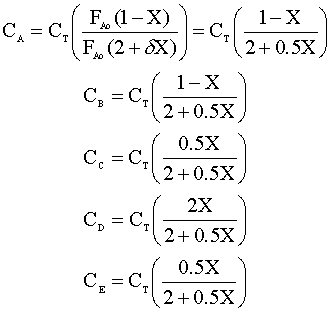
The resulting sketch looks like