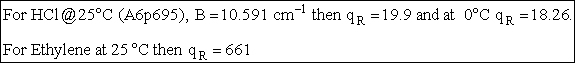Rigid Rotation (A5p409, 413, 557 and A24)
To show
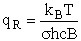(R1)
where
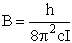= Rotational Constant
(R2)
Consider a particle of mass m rotating about the z axis a distance r from the origin.
(R3)
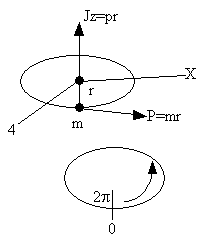
This time we convert the wave equation to spherical coordinate to obtain (A5p410)
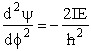(R4)
Classical Energy of a rigid rotator is
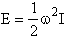(R5)
where w is the angular velocity (rod/s) and I is the
Moment of inertia(A5p555)
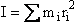(R6)
where mi is the mass located and distance ri from the center of mass.
Quantum mechanics solutions to the
wave equation gives two quantum numbers,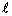 
and
m.
Magnitude of angular momentum
= 
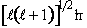
z component of angular momentum = mh
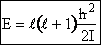(A5p408,p413) (R7)
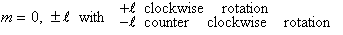
Let J º l
For a linear rigid rotator
E = 
hcB
J (J+ 1) (R8)
Where B is the rotation constant:
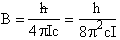(A5p557) (R2)
with
c = speed of light
I = moment of inertia about the center of mass
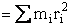
The rotational partition function is
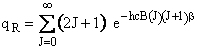(A5p414,563,671) (R9)
Replacing the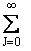 
by an integral from 0 to ¥ and integrating,
we obtain the rotational partition function qR
for a linear molecule (A5p694)
| This is the result we have been looking for! |
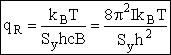(R10)
where Sy is the symmetry number which is the number of different but equivalent arrangements that can be made by rotating the molecules.
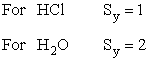
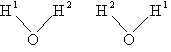
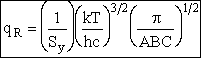
where
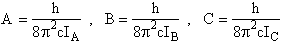
Sy = symmetry number. [For discussion
of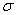 
see Laidler 3rd Ed. p.99.] For a hetronuclear
molecule 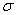= 1 and for a homonuclear diatomic molecule
or a symmetrical linear molecule, e.g., H2,
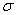then = 2.
Order of Magnitude and Representative Values
