Transition State Theory

Example:� Calculating the Frequency Factor Using Transition State Theory

Use transition state theory to calculate the frequency factor A at 300K for the reaction

�� H + HBr � H₂ + Br

Additional Information Literature values.� (Note:� Most of this information can be obtained from computational chemistry software packages such as Cerius², Spartan or Cache.)

Reactants.� H, HBr

�� H atom (mass)�� 1 amu

�� HBr (mass)�� 80.9 amu

�� HBr vibration wave number�� 2650 cm^�1

�� H � Br separation distance = 142 pm

Transition State Complex.� H�H�Br

�� Vibration wave numbers

�� 2340 cm^�1

�� 460 cm^�1 (degenerate

�� Separation distances

��

Solution

�� The reaction is

�� H + HBr 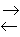�H�H�Br � H₂ + Br

�� The specific reaction rate is

��

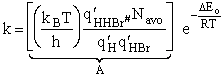
Reactants

�� Hydrogen

��

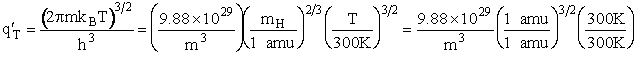
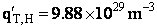
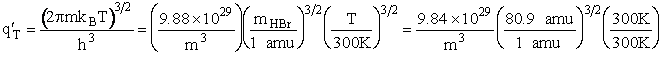
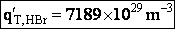
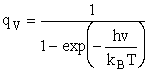
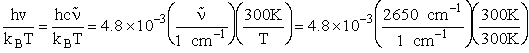
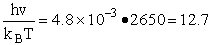
�� Rotation

��

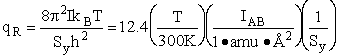
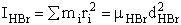
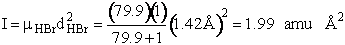
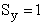
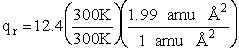
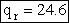
�� Total partition function

��

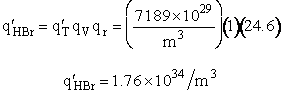
�� Translation

��

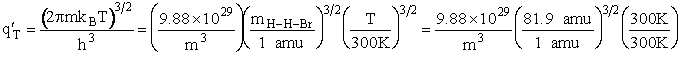
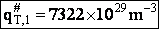
�� Vibration

��

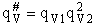
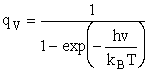
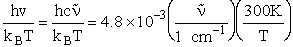
�� 1)�� u = 2340 cm^�1

��

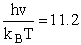
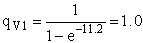
�� 2)�� u = 460 cm²

��

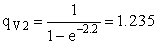
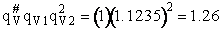
�� Rotation

��

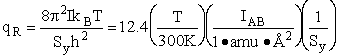
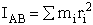
�� Calculate the rotational partition function, 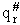, for the transition state shown below.

��

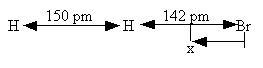
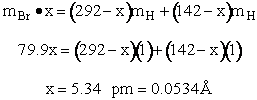
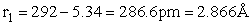
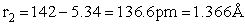
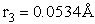
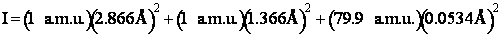
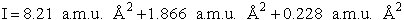
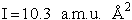
The rotational partition function is

��

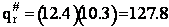
The total partition function for the transition state is

��

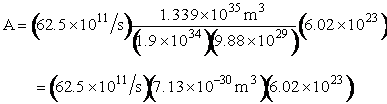
We now calculate the frequency factoring A.

��

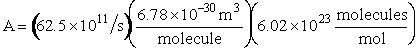
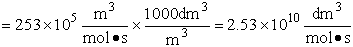
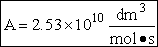
Data From Computational Chemistry

Now let�s calculate A and E using the parameters from cache.

�� For the reaction:

�� H + HBr � H₂ + Br

The 3D potential energy surfaces of the reacting particles along the reaction coordinates was calculated using the MOPAC PM3 method:

��

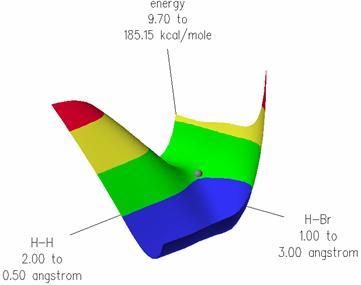
The transition state structure was found at the saddle point, refined by using the DFT/B88-PW91 method as:

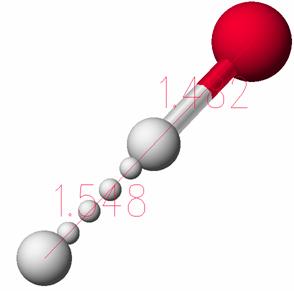
In the transition state, the three atoms are linear and the H-Br distance is 1.48 � while the H-H distance is 1.55 �.

�� The transition state was further proved by vibrational analysis (PM3 FORCE) showing one and only one negative vibration (imaginary frequency of crossing the barrier). Moreover, the negative vibration corresponds to the movement of the atoms on the two reaction coordinates.

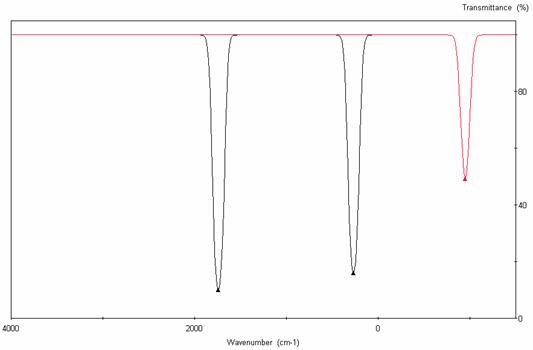
Summary of Information from Cache Software

Reactants.� H, HBr

�� H atom (mass)�� 1 amu

�� HBr (mass)�� 80.9 amu

�� HBr vibration wave number�� 2122 cm^�1

�� H � Br separation distance = 147 pm

Transition State Complex.� H�H�Br

�� Vibration wave numbers

�� 1736 cm^�1

�� 289 cm^�1

�� Separation distances

��

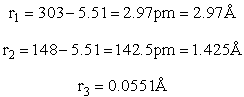
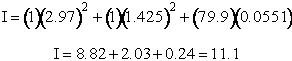
�� q_r = 137.5

��

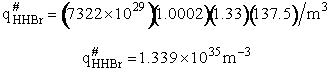
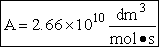
Chemical	Heat of formation at 298K (kcal/mol)		Energy of zero point level (a.u.)
Chemical	MOPAC PM3 method	Experiments	DFT/B88-PW91 method
HBr	5.3	-8.71	-2574.451933
H	52.1	52.1	-0.502437858
H-H-Br Transition state	59.6	N/A	-2574.953345

Therefore, the standard enthalpy of activation is:

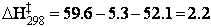�� kcal/mol = 9.2 kJ/mol

The intrinsic Arrhenius activation energy is:

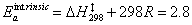�� kcal/mol = 11.7 kJ/mol

Barrier height E₀ (difference between zero-point levels of activated complexes and reactants) (because the conversion between the a.u. and the kcal/mol units is very large, we need to maintain a high number of decimal point):

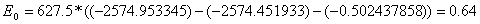�kcal/mol = 2.7 kJ/mol

Return to Transition State Theory