(Ecological engineering) Several researchers have examined
the feasibility of using wetlands to clean up high volumes of polluted water. Experiemental
wetland three (EW3) at the Des Moines Experimental Wetlands site in Illinois has
a volume of 15,000,000 dm3 and an inflow of 70,000
dm3 of water per house from the Des Plaines Rier.
The outflow eventually returns to the river. During late spring, the river water
typically contains 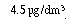 of the herbicide atrazine. However,
the maximum contaminant level (MCL) under the federal Drinking Water Act is
of the herbicide atrazine. However,
the maximum contaminant level (MCL) under the federal Drinking Water Act is 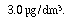 As a first approximation treat EW3 as a perfectly mixed CSTR and assume that atrazine
decomposition is first order with k= 0.0025 h -1.
As a first approximation treat EW3 as a perfectly mixed CSTR and assume that atrazine
decomposition is first order with k= 0.0025 h -1.
(a) First consider that EW3 contains water but no atrazine
at the time the flow fromthe river is diverted. Plot C A as a function
of t for the case where the outflow is kept equal to inflow. After what time
does C A reach 99% of its steady-state value? Is it below the MCL?
(b) Next consider the case where EW3 initially contains neither atrazine nor
water. Outflow is kept at 50,000 dm 3 /h for 750 h.
after which it becomes 70,000 dm 3 /h. Plot the concentration
as a function of time and explain how it differs from the plot in part (a). Plot
the number of moles of atrazine in EW3 versus time. Why is N A increasing
while C Aversus time is decreasing?
(c) EW3 is operating initially at the steady-state conditions found in part
(a). Suppose that weekly thunderstorms periodically increase the amount of atra zine
leached into the Des Plaines River, thereby increasing the concentration in the inflow
to EW3. Concentration as a function of time is given by
.gif)
where the trigonometric argument is in radians. Plot C A0 and C A versus t on the same graph. Does the outflow exceed the MCL at any time? Do C A0 and C A reach their maximums and minimums at the same times? Does C Aever exceed C A0? How can this be?
(d) EW3 is operating initially at the steady-state conditions
found in part (a). Suppose that there is a drought lasting 1000 h during which the
evaporative flux of water from EW3 is 10,000 dm 3 /h.
The overall water balance is such that the wetland volume remains constant, however.
No atrazine leaves via evaporation. What does the concentration profile look like?
How can this be explained?
The cells in your body need to obtain nutrients, hormones, growth factors, and other molecules present in very low concentrations in the fluid around them. To avoid engulfing a large quantity of this fluid and then intracellularly separating useful from useless molecules, the cells possess what are known as receptors on their surface. These receptors are able to bind interesting molecules or ligands with high affinity, thus capturing molecules for the cell's use (Figure CDP4-C).
(a) You are growing 10 6 cells/mL in a T flask containing 10 mL of media. Each cell has 10
5 receptors on its surface. The association
rate constant 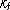 for the binding of ligands to receptors is 10 6 M -1 min-1 . Calculate the time for 50% of the receptors
to bind ligands if you add ligands at a concentration of 10 -7 M. Assume irreversible binding and perfect mixing.
for the binding of ligands to receptors is 10 6 M -1 min-1 . Calculate the time for 50% of the receptors
to bind ligands if you add ligands at a concentration of 10 -7 M. Assume irreversible binding and perfect mixing.
(b) Show that the ligand concentration in part (a) is sufficiently in excess
so that the binding could be considered pseudo-first order.
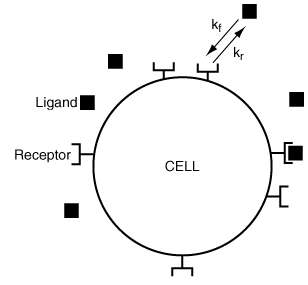
Figure CDP4-C
(c) The binding of ligand to receptor is actually a reversible reaction. For the binding of your ligand to receptors, the dissociation rate constant k r is 0.1 min -1 . Using the approximation justified in part (b) and assuming perfect mixing, calculate the percentage of receptors bound 5 min after you add the ligand to the media. (J. Linderman, University of Michigan)
[2nd Ed. P4-34]
(Batch bromination of p-chlorophenyl isopropyl ether) You
are in charge of the production of specialty chemicals for your organization and
an order comes in for 3 lb of brominated p-chlorophenyl isopropyl ether. You
decide to use the technique reported by Bradfield et al. [J. Chem. Soc., 1389
(1949)], who carried out the reaction in 75% acetic acid at 68°F. You have a
batch reactor that holds 5 gal (0.670 ft 3
) of a reacting mixture that can be used. Starting out with a mixture that
contains 0.002 lb mol (0.34 lb) of p-chlorophenyl isopropyl ether and 0.0018
lb mol (0.288 lb) of bromine in the 5 gal, you decide to run 10 batches of the mixture
to 65% conversion of the p-chlorophenyl isopropyl ether. This procedure will
give the desired 3 lb. How long will each batch take?
Additional information:
Kinetics (from Bradfield et al.):
Reaction: 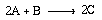
where A is p-chlorophenyl isopropyl ether, B is bromine, and C is monobrominated product .
Rate Law: 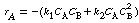
Specific reaction rates at 68°F:
k 1 = 1.98 ft 3 /lb
mol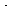 min
min
k2 = 9.2 x 10 3 (ft 3
/lb mol) 2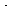 min -1
min -1
[2nd Ed. P4-29]
A liquid organic substance, A, contains 0.1 mol % of an impurity, B, which can be hydrogenated to A:
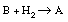
The material is purified by hydrogenation as a liquid in a continuous well-mixed reactor at 100°C. The feed rate of the liquid is constant at 730 lb/h. The reactor holds 50 gal of liquid, at 500 psig, and the amount of B in the product levels out at 0.001 mol %. What will be the concentration of B in the product if the hydrogen pressure is held at 300 psig? Assume that the reaction behaves as though it were first order with respect to both B and H 2 , that is, in batch,
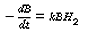

Assume perfect gas laws and Henry's law. Also assume the following
properties:

[2nd Ed. P4-15]
The gas-phase reaction 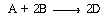 is
to be carried out in an isothermal plug-now reactor at 5.0 atm. The mole fractions
of the feed streams are A = 0.20, B = 0.50, and inerts = 0.30.
is
to be carried out in an isothermal plug-now reactor at 5.0 atm. The mole fractions
of the feed streams are A = 0.20, B = 0.50, and inerts = 0.30.
(a) What is the steady-state volumetric flow rate at any
point in the reactor if the pressure drop due to fluid friction can be ignored? [Ans.:
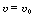 (1 - 0.2X).]
(1 - 0.2X).]
(b) What are the expressions for the concentrations of A, B, and D as a function
of conversion at any point along the reactor?
(c) What is the feed concentration (units: mol/ dm 3
) of A if the feed temperature is 55°C?
(d) Determine how large the plug-flow reactor must be to achieve a conversion
(based on A) of 0.70 if the temperature in the reactor is uniform (55°C), the
volumetric feed rate is 50 dm 3 /min,
and the rate law at 55°C is
-r = 2.5 C A(1/2) C B kmol/m 3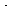 min
min
(Ans.: V = 50.21 dm 3.)
(e) Plot the concentrations, volumetric flow rate, and conversion
as a function of reactor length. The reactor diameter is 7.6 cm.
(f) How large would a CSTR have to be to take the effluent from the PF reactor
in part (d) and achieve a conversion of 0.85 (based on the feed of A to the plug-flow
reactor) if the temperature of the CSTR is 55°C?
(g) How many 1-in.-diameter pipe tubes, 20 ft in length, packed with a catalyst,
are necessary to achieve 95% conversion of A starting with the original stream? Plot
the pressure and conversion as a function of reactor length. The particles are 0.5
mm in diameter and the bed porosity is 45%.
(h) Calculate the PFR size to achieve 70% of the equilibrium conversion and
the CSTR size necessary to raise the conversion of the PFR effluent to 85% of the
equilibrium conversion if their temperatures were uniform at 100°C. The activation
energy for the reaction is 30 kJ/mol, and the reaction is reversible with an equilibrium
constant at 100°C of 10 (m 3 /kmol) 1/2
. (Ans: V PFR = 8.56 dm
3 , V CSTR
= 6.45 dm 3 )
[2nd Ed. P4-8]
You are designing a reactor system for carrying out the constant-density liquid-phase reaction
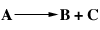
which has the rate law
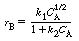
(a) What system (i.e., type and arrangement) of flow reactors,
either one alone or two in series, would you recommend for continuous processing
of a feed of pure A in order to minimize the total reactor volume? (90% conversion
of A is desired.)
(b) What reactor size(s) should be used?
(c) Plot the conversions and concentrations of A and B as a function of plug-flow
reactor volume.
Additional information:
k1 = 10.0 (lb-mol/ft 3) 0.5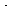 h -1
h -1
k 2 = 6.0 ft 3/lb mol
feed = 100 lb mol/h of pure A
C AO = 0.25 lb mol/ft 3
total pressure = 2000 kPa
[1st Ed. P4-14]
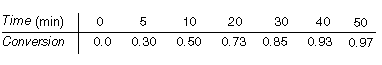
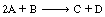 is carried out in a semibatch reactor. The reactor volume is 1.2 m
3 . The reactor initially contains 5 mol
of B at a concentration of 0.015 kmol/m 3
. A at an aqueous concentration of 0.03 kmol/m 3
is fed to the reactor at a rate of 4 dm 3
/min. The reaction is first order in A and half order in B with a specific
reaction rate of k = 6 (m 3 /kmol)
1/2 / min. The activation energy is 35 kJ
/mol. The feed rate to the reactor is discontinued when the reactor contains 0.53
m 3 of fluid.
is carried out in a semibatch reactor. The reactor volume is 1.2 m
3 . The reactor initially contains 5 mol
of B at a concentration of 0.015 kmol/m 3
. A at an aqueous concentration of 0.03 kmol/m 3
is fed to the reactor at a rate of 4 dm 3
/min. The reaction is first order in A and half order in B with a specific
reaction rate of k = 6 (m 3 /kmol)
1/2 / min. The activation energy is 35 kJ
/mol. The feed rate to the reactor is discontinued when the reactor contains 0.53
m 3 of fluid.
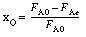
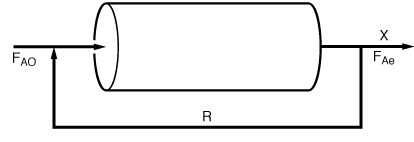
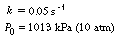
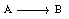
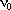 0
= 10 dm 3 /s. The specific reaction
rate is k = 0.25 s -1 .
0
= 10 dm 3 /s. The specific reaction
rate is k = 0.25 s -1 .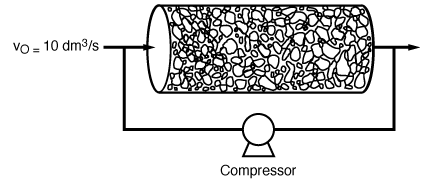
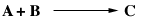 is carried out isothermally at 570°C and 1 atm. A part of the condenser unit
is heated to reactor temperature and recycled to reactor inlet. The pressure drop
in the conduits can be assumed to be negligible. Estimate the reactor volume for
50% converstion of the feed F A0 .
is carried out isothermally at 570°C and 1 atm. A part of the condenser unit
is heated to reactor temperature and recycled to reactor inlet. The pressure drop
in the conduits can be assumed to be negligible. Estimate the reactor volume for
50% converstion of the feed F A0 .
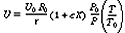
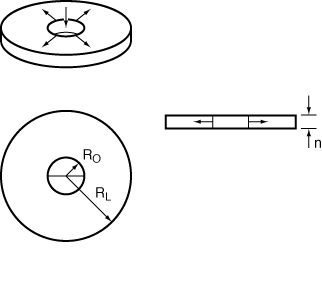
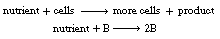
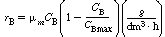
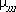 and C MAX
are constant rate law parameters.
and C MAX
are constant rate law parameters. ,
takes place in a homogeneous liquide system. Reactants and products are mutually
soluble, and the volume change as a result of reaction is negligible. Feed to a tubular
(plug-flow) reactor that operates essentially isothermally at 260°F consists
of 210 lb/h of A and 260 lb/h of B. Total volume of the reactor is 5.33 ft 3
, and with this feed rate, 50% of compound A in the feed is converted. It
is proposed that to increase conversion, a stirred reactor of 100-gal capacity be
installed in series with, and immediately upstream of, the tubular reactor. If the
stirred reactor operates at the same temperature, estimate the conversion of A that
can be expected in the revised system; neglect the reverse reaction. Other available
data include:
,
takes place in a homogeneous liquide system. Reactants and products are mutually
soluble, and the volume change as a result of reaction is negligible. Feed to a tubular
(plug-flow) reactor that operates essentially isothermally at 260°F consists
of 210 lb/h of A and 260 lb/h of B. Total volume of the reactor is 5.33 ft 3
, and with this feed rate, 50% of compound A in the feed is converted. It
is proposed that to increase conversion, a stirred reactor of 100-gal capacity be
installed in series with, and immediately upstream of, the tubular reactor. If the
stirred reactor operates at the same temperature, estimate the conversion of A that
can be expected in the revised system; neglect the reverse reaction. Other available
data include:

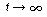 )?
(Ans.: NA = 200 mol) Explain why the number of moles remains virtually
constant at long times.
)?
(Ans.: NA = 200 mol) Explain why the number of moles remains virtually
constant at long times.