Solution
Recalling Example 5-1, the combined mole balance and rate law for a constant-volume batch reactor can be expressed in the form![]()
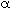 = 0, for which equation (ES-1.5) becomes
= 0, for which equation (ES-1.5) becomes ![]()
![]()
Assuming a zero-order reaction
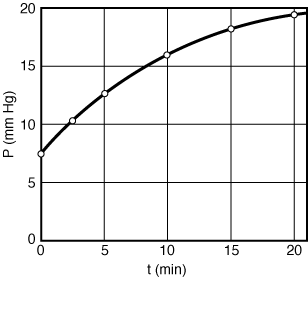
Figure CDE5-1-1
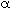 = 2:
= 2: ![]()
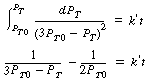
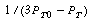 versus t should be linear:
versus t should be linear: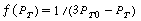
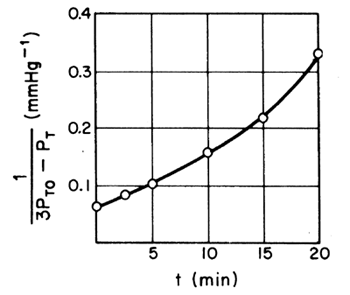
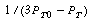 versus t was constructed and is shown in Figure CDE5-1.2. From the curvature of the plot, we conclude that the reaction is not second order.
versus t was constructed and is shown in Figure CDE5-1.2. From the curvature of the plot, we conclude that the reaction is not second order. 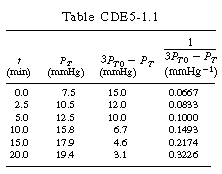
 = 1). If zero, first, or second order do not seems to describe the reaction rate equation, it is usually best to try some other method of determining the reaction order. for
= 1). If zero, first, or second order do not seems to describe the reaction rate equation, it is usually best to try some other method of determining the reaction order. for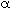 = 1,
= 1,![]()
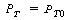 when t = 0 yields
when t = 0 yields 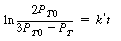
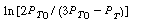 versus t should be linear. After completing Table CDE5-1.2 using the raw data, a plot of
versus t should be linear. After completing Table CDE5-1.2 using the raw data, a plot of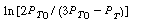 as a function of time is made using semilog paper as shown in Figure CDE5-1.3. From the plot we see that
as a function of time is made using semilog paper as shown in Figure CDE5-1.3. From the plot we see that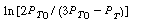 is indeed linear with time, and we therefore conclude that the decomposition of di-tert-butyl peroxide follows first-order kinetics. From the slope of the plot in Figure CDE5-1.3, we can determine the specific reaction rate, k = 0.08 min -1
is indeed linear with time, and we therefore conclude that the decomposition of di-tert-butyl peroxide follows first-order kinetics. From the slope of the plot in Figure CDE5-1.3, we can determine the specific reaction rate, k = 0.08 min -1 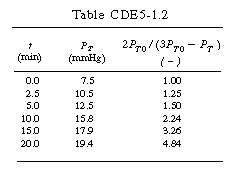
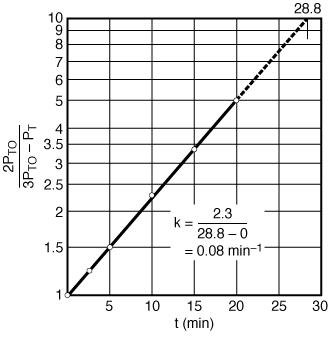
Figure CDE5-1.3