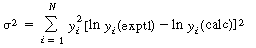|
|
|
|
|
|
|
Both the linear and nonlinear least-squares analyses presented assume
that the variance is constant throughout the range of the measured variables. If
this is not the case, a weighted least-squares analysis must be used to obtain better
estimates of the rate law parameters. If the error in measurement is at a fixed level,
the relative error in the dependent variable will increase as the independent variable
increases (decreases). For example, in a first-order decay reaction
(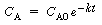 ),
if the error in concentration measurement is 0.01 CA0,
the relative error in the concentration measurement [0.01 CA0/CA(t)
] will increase with time. When this error condition occurs the sum
to be minimized for N measurements is ),
if the error in concentration measurement is 0.01 CA0,
the relative error in the concentration measurement [0.01 CA0/CA(t)
] will increase with time. When this error condition occurs the sum
to be minimized for N measurements is |
|
|
|
|
|
|
|
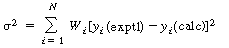
|
|
|
|
|
|
|
|
where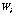 is a weighting factor. is a weighting factor.
For parameter estimation involving exponents, it has been shown that a weighted
least-squares analysis is usually necessary.1
Two such cases that occur in the analysis of chemical reaction engineering
data are concentration-time data for an irreversible first-order reaction, |
|
|
|
|
|
|
|
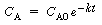
|
|
|
|
|
|
|
|
and reaction rate-temperature data,2
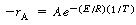
In general, these equations are of the form
|
|
|
|
|
|
|
|
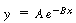
|
|
|
|
where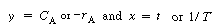 , ,
respectively
|
|
|
|
|
|
|
|
Linearizing, we obtain |
|
|
|
|
|
|
|
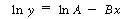
|
|
|
|
|
|
|
|
We want to find the values of A and B that minimize
the weighted sum of squares. For a semilog arithmetic transformation, the
weighting function is just the square of the independent variable itself3
(i.e.,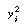 ). The
function to be minimized is ). The
function to be minimized is |
|
|
|
|
|
Weighted least
squares
|
|
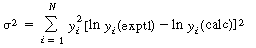
|
|
|
|
|
|
|
|
There are also strategies available that suggest
the experimental conditions to be used for each succeeding data point in
order to converge most rapidly to the best values of the rate law parameters
(Box et al.).4
|
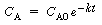 ),
if the error in concentration measurement is 0.01 CA0,
the relative error in the concentration measurement [0.01 CA0/CA(t)
] will increase with time. When this error condition occurs the sum
to be minimized for N measurements is
),
if the error in concentration measurement is 0.01 CA0,
the relative error in the concentration measurement [0.01 CA0/CA(t)
] will increase with time. When this error condition occurs the sum
to be minimized for N measurements is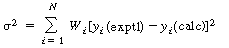
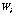 is a weighting factor.
is a weighting factor.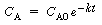
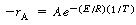
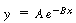
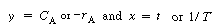 ,
,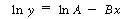
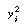 ). The
function to be minimized is
). The
function to be minimized is