
The rate law for this reaction will be of the form:
Where subscript "A" refers to the reactant HbO2. Also, n = the order of the reaction and k = the specific reaction rate constant. These are the two parameters we need to find using the data given.
Since the values of percent decomposition of HbO2 has been given, we can evaluate the conversion XA of the reaction (XA = % decomposition/100). Therefore, we need to express the rate law in terms of conversion as follows.

Where FA0 and CA0 are the the inlet molar flow rate and the feed concentration, respectively.
Now dV = Acdz, where Ac is the tube cross-sectional area (= 0.0196 cm2). Further simplifying the rate equation leads to
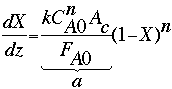
where a is a lumped parameter containing k, n, FA0, and CA0. To evaluate the two parameters n and k, we first need to plot ln(dXA/dz) vs. ln(1-XA). We can estimate the values of dXA/dz by first calculating the X/
X/ z, and then interpolating the dX/dz values graphically, as shown below.
z, and then interpolating the dX/dz values graphically, as shown below.
| Electrode Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Position (cm) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
 z (cm) z (cm)
|
5 | 5 | 5 | 5 | 5 | 5 | 5 |
| Conversion of HbO2 (XA) | 0.0000 | 0.0193 | 0.0382 | 0.0568 | 0.0748 | 0.0925 | 0.110 |
| (1-XA) | 1.0000 | 0.9807 | 0.9618 | 0.9432 | 0.9252 | 0.9075 | 0.8900 |
 X X
|
- | 0.0193 | 0.0189 | 0.0186 | 0.018 | 0.0177 | 0.0175 |
 X/ X/ z z
|
- | 0.00386 | 0.00378 | 0.00372 | 0.00360 | 0.00354 | 0.00350 |
A histogram plot of X/
X/ z vs. z is then produced. The values of dX/dz are evaluated using equal-area graphical differentiation as described in the appendix section:
z vs. z is then produced. The values of dX/dz are evaluated using equal-area graphical differentiation as described in the appendix section:
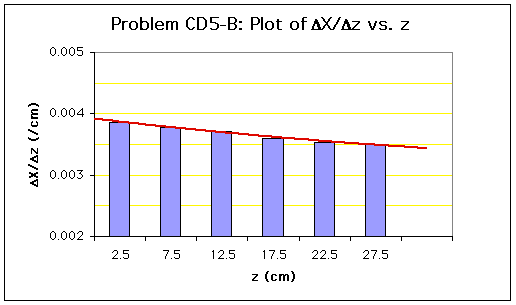
The values of dXA/dz at electrode points can be estimated from the equal-area line:
| Electrode Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| dX/dz | 0.00391 | 0.00382 | 0.00373 | 0.00365 | 0.00358 | 0.003514 | 0.00346 |
Using the values obtained above, a plot of ln(dXA/dz) vs. ln(1-XA) is produced:
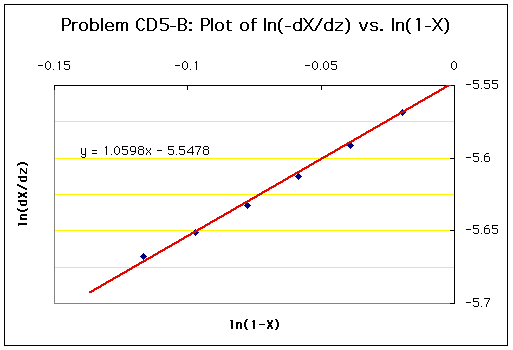
As can be seen from this plot, the data points are nearly linear. The best-fit line is drawn in the plot, and the slope is 1.06. This slope corresponds to the order of the rate law (n), which can be approximated to be 1. Therefore, the rate law is now:
To calculate k, the specific reaction rate constant, we must employ the following relationship, using the data gathered at an electrode point (e.g., at p = 2):
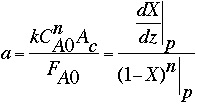
All the values in the relationship are known, except k, FA0, and CA0. The values for the latter two can be estimated using the hint immediately following the problem statement. According to the hint, the inlet molar concentration of HbO2 can be estimated by using the typical values listed in the literature for hemoglobin concentration in the human blood (150 g of hemoglobin per liter of blood; molecular weight of hemoglobin = 64500)1,2. Therefore, CA0 = 2.33 x 10-6 moles/cm3, and FA0 = 45.67 x 10-6 moles/s. Substituting these values in the above expression leads to:
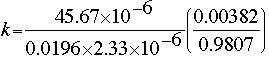
Therefore, the specific reaction rate is 3.8953 s-1, and the final reaction rate law is:
1 D. Voet and J.G. Voet, "Biochemistry", John Wiley & Sons, New York (1990).
2 A.L. Lehninger, "Principles of Biochemistry", Worth Publishers,
New York (1982).
Back to Problem Statement