Using the PSSH, develop a rate law for the rate of formation of HBr for the mechanism given by Equations (CD7-3), (CD7-4), and (CD7-6) through (CD7-8).
Solution
Each reaction is to be considered elementary. First we write down the net rate of formation of the product resulting from all the reaction steps:
Rate of formation
of HBr
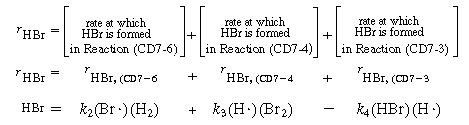
(CDE7-2.1)
(CDE7-2.2)
The intermediate species Br![]() and H
and H![]() are free radicals, which are present in low concentrations and highly reactive. Consequently, the use of the PSSH is justified. We next write the net rate of formation of the intermediate species and set these rates equal to zero (rH
are free radicals, which are present in low concentrations and highly reactive. Consequently, the use of the PSSH is justified. We next write the net rate of formation of the intermediate species and set these rates equal to zero (rH = 0, rBr
= 0, rBr![]() = 0).
= 0).
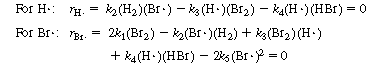
(CDE7-2.4)
Adding Equations (CDE7-2.3) and (CDE7-2.4) gives
(Br ) as a function of (Br2)
) as a function of (Br2)
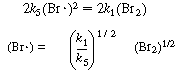
Subtracting Equation (CDE7-2.3) from (CDE7-2.2) gives
rHBr= 2k3 (H )(Br2)
)(Br2)
To eliminate (H![]() ) from this equation, rewrite Equation (CDE7-2.3) as
) from this equation, rewrite Equation (CDE7-2.3) as
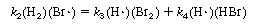
and solve for (H![]() ):
):
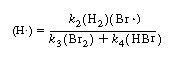
To eliminate (Br ), we use Equation (CDE7-2.5) to obtain
), we use Equation (CDE7-2.5) to obtain
(H ) as a function of reactants and products
) as a function of reactants and products
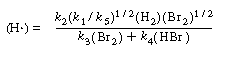
Substituting Equation (CDE7-2.9) into Equation (CDE7-2.6), we see that
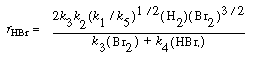
We can rewrite Equation (CDE7-2.10) in the form
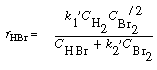
By comparing Equations (CDE7-2.6) and (CDE7-2.11) we again see that the mechanism produces a rate law consistent with experimental observation!