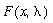 , in which x is a scalar variable and
, in which x is a scalar variable and 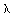 is a parameter. Figure CD8-1 shows curves (AB, BC, and BD) for which
is a parameter. Figure CD8-1 shows curves (AB, BC, and BD) for which
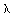 that will satisfy Equation (CD8-1). However, as we continue to increase along AB, we reach a bifurcation point * beyond which there are two values of x that satisfy Equation (CD8-1) for a given value of
that will satisfy Equation (CD8-1). However, as we continue to increase along AB, we reach a bifurcation point * beyond which there are two values of x that satisfy Equation (CD8-1) for a given value of 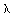 . Consequently, we analyze our system of equations to learn if a bifurcation point exists that denotes multiple solutions.
. Consequently, we analyze our system of equations to learn if a bifurcation point exists that denotes multiple solutions. There is another condition that is necessary for a bifurcation point to exist. If we were to move an incremental amount
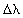 away from the bifurcation point but still remain on BC or BD, we would have
away from the bifurcation point but still remain on BC or BD, we would have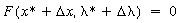
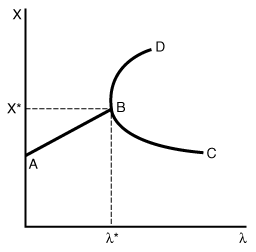
Figure CD8-1
Bifurcation point.
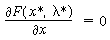
We shall continue the discussion of the first-order reaction taking place in a CSTR to illustrate bifurcation analysis. A slight rearrangement of a combination of Equations (8-68) and (8-69) from the energy balance gives
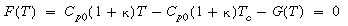
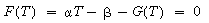
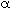 and
and 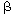 are positive constants.
are positive constants.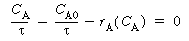
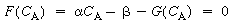
(CD8-7)
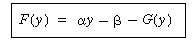
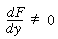
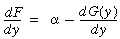
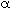 . Thus the sufficient condition for uniqueness is
. Thus the sufficient condition for uniqueness is
Uniqueness
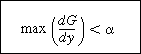
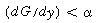 , we do not know at this point whether or not multiple solutions exist and we must carry the analysis further.
, we do not know at this point whether or not multiple solutions exist and we must carry the analysis further. 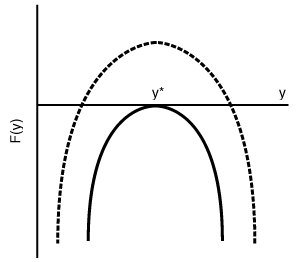
Figure CD8-2
MSS with a parabolic function.
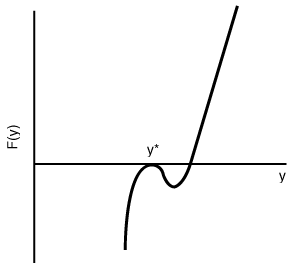
Figure CD8-3
F(y ) curve common to chemically reacting systems.
We now apply the condition for a bifurcation point, Equations (CD8-1) and (CD8-3), to the CSTR balances, that is, Equation (CD8-8). If multiple steady states exist, there will be a bifurcation point, y*, at which the following conditions are satisfied:
Conditions for
multiple steady states
multiple steady states
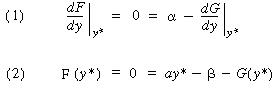
(CD8-12)