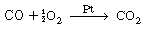
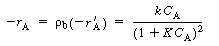
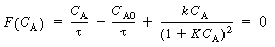
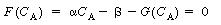
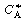
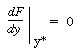
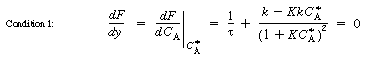
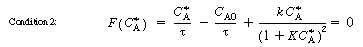
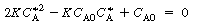
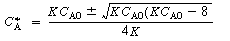
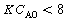 , no real roots exist and there
are no possible steady states. A rearrangement of Equation (CDE8-1.4) gives
, no real roots exist and there
are no possible steady states. A rearrangement of Equation (CDE8-1.4) gives
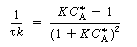
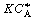 is increased from 1. To find
this maximum we set the derivative of the right-hand side of Equation (CDE8-3.8)
with respect to CA equal to zero, and solve to find that the maximum occurs at
is increased from 1. To find
this maximum we set the derivative of the right-hand side of Equation (CDE8-3.8)
with respect to CA equal to zero, and solve to find that the maximum occurs at
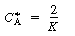
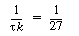
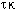 is smaller than 27. Equation CDE8-3.10 can never be satisfied
and there will be no MSS. Figure CDE8-1.1 shows a mapping of those regions where
no multiple steady states will exist.
is smaller than 27. Equation CDE8-3.10 can never be satisfied
and there will be no MSS. Figure CDE8-1.1 shows a mapping of those regions where
no multiple steady states will exist.
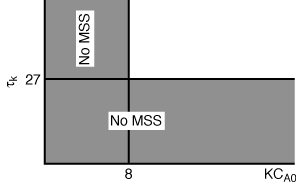
Figure CDE8-3.1
Mapping the regions of no multiple steady states.
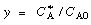 , Equation (CDE8-3.6) can be
written as
, Equation (CDE8-3.6) can be
written as
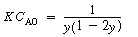
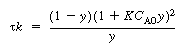
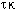 . The
shaded area shows the combinations of these variables that will produce multiple
steady states.
. The
shaded area shows the combinations of these variables that will produce multiple
steady states.
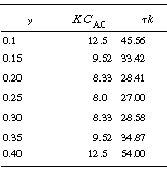
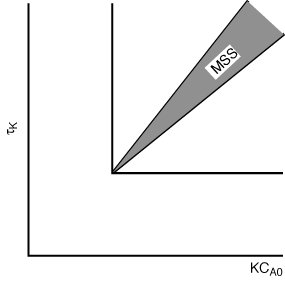
Figure CDE8-3.2
Region of possible multiple steady states.