Tert-Amyl Methyl Ether (TAME) is an oxygenated additive for green gasolines. Besides its use as an octane enhancer, it also improves the combustion of gasoline and reduces the CO and HC (and, in a smaller extent, the NOx) automobile exhaust emissions. Due to the environmental concerns related to those emissions, this and other ethers (MTBE, ETBE, TAEE) have been lately studied intensively.
TAME is currently catalytically produced in the liquid phase by the reaction of methanol (MeOH) and the isoamylenes 2-methyl-1-butene (2M1B) and 2-methyl-2-butene (2M2B). There are three simultaneous equilibrium reactions in the formation and splitting of TAME: the two etherification reactions and the isomerization between the isoamylenes:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
These reactions are to be carried out in a plug flow reactor and a membrane reactor in which MeOH is fed uniformly through the sides.
For isothermal operation:
a) Plot the concentration profiles for a 10 m3 PFR.
b) Vary the entering temperature, T0, and plot the exit concentrations as a function of T0.
For a reactor with heat exchange (U = 10 J.m-2.s-1.K-1):
c) Plot the temperature and concentration profiles for an entering temperature of 353 K
d) Repeat (a) through (c) for a membrane reactor.
NOTE: To simplify the problem, consider the solution density and heat capacity constant (evaluate them for the entering temperature and the feed mole fractions) and consider the solution as ideal: ai = xi in the rate expressions.
A new and improved kinetic model, including the non-ideal character of the reacting solution, can be found in “Number of Actives Sites in TAME Synthesis: Mechanism and Kinetic Modeling”, Manuela V. Ferreira and José M. Loureiro, Ind. Eng. Chem. Res. 43 (2004) 5156-5165.
Additional information for solving the problem
equilibrium constants, activity based (Vilarinho Ferreira and Loureiro, 2001)
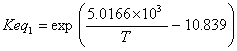 (I.1)
(I.1)
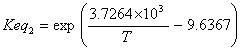 (I.2)
(I.2)
![]() (I.3)
(I.3)
with: T in Kelvin
Kinetic constants for the direct reactions (Kiviranta-Pääkkönen et al., 1998)
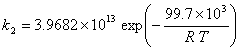 (I.5)
(I.5)
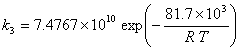 (I.6)
(I.6)
with: k in mol.![]() .s-1
.s-1
T in Kelvin
R = 8.314 J.mol-1.K-1
Adsorption constants for each component, activity based (calculated and adapted from Oktar et al., 1999)
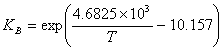 (I.7)
(I.7)
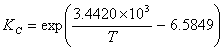 (I.8)
(I.8)
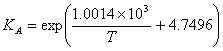 (I.9)
(I.9)
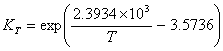 (I.10)
(I.10)
with: T in Kelvin
Heat of reaction (Vilarinho Ferreira and Loureiro, 2001)
![]() = - 41.708 kJ.mol-1
= - 41.708 kJ.mol-1
![]() = - 30.981 kJ.mol-1
= - 30.981 kJ.mol-1
![]() = - 10.727 kJ.mol-1
= - 10.727 kJ.mol-1
Bulk density and bed porosity
The PFR is filled with a macroreticular strong cation ion-exchange resin in hydrogen form (Amberlyst 15 Wet, Rohm & Haas).
![]()
The bed porosity is: e
· Rate equations for the formation of each component (Vilarinho Ferreira and Loureiro, 2001)
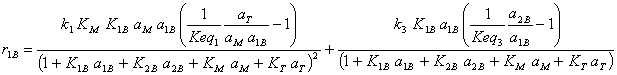 (I.11)
(I.11)
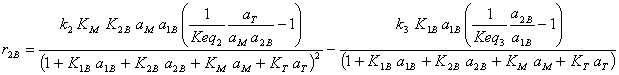 (I.12)
(I.12)
![]() (I.13)
(I.13)
![]() (I.14)
(I.14)
with: r in mol.![]() .s-1
.s-1
ai stands for the activity of component i in the liquid phase, and since we are considering the solution as ideal:
![]() (I.15)
(I.15)
where xi is the mole fraction of component i in the liquid phase.
We can also define the rate of each reaction:
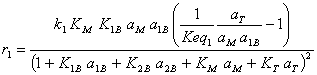 (I.16)
(I.16)
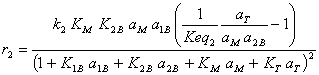 (I.17)
(I.17)
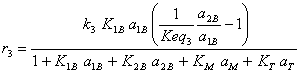 (I.18)
(I.18)
Heat capacity of each component
![]() (I.19)
(I.19)
with: Cp in kJ.mol-1.K-1
T in Kelvin
|
component i |
Symbol |
ai |
104 bi |
107 ci |
1010 di |
|
MeOHa |
A |
0.077 |
1.62 |
2.06 |
2.87 |
|
2M1Bb |
B |
1.27 |
-0.609 |
5.08 |
1.69 |
|
2M2Bb |
C |
1.33 |
-1.48 |
7.51 |
-0.882 |
|
TAMEc |
T |
1.73 |
2.29 |
-6.00 |
20.0 |
aZhang and Datta, 1995; bKitchaiya and Datta, 1995; cEstimated by the Missenard
To simplify the problem we are going to consider the heat capacity of each component constant and equal to its value at the entry conditions: T = T0.
The solution heat capacity will also be considered constant and equal to its value at the entry conditions:
i
1,i
2,i
3,i
4,i
To simplify the problem we are going to consider the heat capacity of each component constant and equal to its value at the entry conditions: T = T0.
The solution density will also be considered constant and equal to its value at the entry conditions:
Writing mass and energy balances
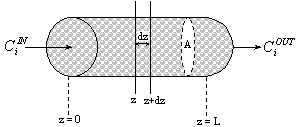
In the figure is a
representation of a PFR filled with a catalyst.
Fig.
1:Representation of a PFR filled with catalyst.
A.
Steady state mass balance For the
steady state mass balance of component i, in the volume element of length dz,
we can write: If e is the bed porosity, the area, A,
available for the catalyst particles is [(1-e) A] and the area available for the fluid is [e A]. Equation (A.1) becomes: where ji is the molar flux of
component i, rb
is the bulk density and ri is the rate of formation of
component i. Re-writing
equation (A.2):
Starting solving the problem
![]() (A.1)
(A.1)
![]() (A.2)
(A.2)![]() (A.3)
(A.3)
Considering a plug flow with axial dispersion, the molar flux is given by:
where ui is the interstitial velocity of the fluid, Ci is the concentration of component i in the fluid and Dax is the axial dispersion coefficient.
Normalizing some
of the variables: ![]() (L is the PFR length),
(L is the PFR length), ![]() (
(![]() where
where ![]() is the feed
concentration of component i),
is the feed
concentration of component i),
dividing by ![]() , equation
(A.7) becomes:
, equation
(A.7) becomes:
where Pe
is the dimensionless Peclet number given by ![]() , and t is the space-time given by
, and t is the space-time given by ![]() .
.
Grouping the
term ![]() as
a reaction term represented by
as
a reaction term represented by ![]() , the steady state mass balance
of component i becomes:
, the steady state mass balance
of component i becomes:
![]() (A.9)
(A.9)
In the limiting case of absence
of dispersion ![]() , equation (A.9) becomes:
, equation (A.9) becomes:
![]() (A.10)
(A.10)
B. Steady state energy balance
For the steady state energy balance in the volume element of length dz, considering no dispersion, we can write:
![]() (B.1)
(B.1)
where jh is the heat flux, ![]() is the heat
of reaction j, rj is the rate of reaction j, Alat
is the lateral area of the volume element, U is the overall
heat-transfer coefficient, T is the reactor temperature and Tw
is the reactor wall temperature.
is the heat
of reaction j, rj is the rate of reaction j, Alat
is the lateral area of the volume element, U is the overall
heat-transfer coefficient, T is the reactor temperature and Tw
is the reactor wall temperature.
Re-writing equation (B.2):
The heat flux can be given by:
where r is the solution density and Cp is the solution heat capacity.
If R0 is the reactor radius, the lateral area of the volume element of length dz is:
and its sectional area is:
leading to:
Substituting into equation (B.3):
Normalizing the
space variable: ![]() , remembering the space-time
definition
, remembering the space-time
definition ![]() and
rearranging equation (B.8):
and
rearranging equation (B.8):
The term ![]() is
dimensionless and is referred as NTU (number of heat transfer units).
is
dimensionless and is referred as NTU (number of heat transfer units).
Finally, the steady state energy balance becomes:
C. Boundary Conditions
In the absence of dispersion, we only need one boundary condition:
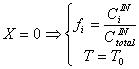 (C.1)
(C.1)
where T0 is the initial reactor temperature.
Algorithm to solve the problem
We have a non-linear system of Ordinary Differential Equations (ODE) to solve:
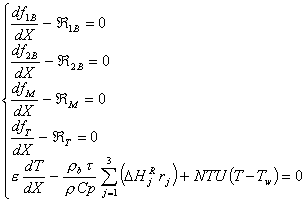 (1)
(1)
The program we developed uses subroutine DDASSL (Brenan et al., 1989) to solve this system. This code solves a system of differential/algebraic equations of the form delta(t, y, yprime)=0, with delta(i) = yprime(i) – y(i), using the backward differentiation formulas of orders one trough five. t is the current value of the independent variable (in our case t = X), y is the array that contains the solution components at t (in our case we have: y(i) = f(i), i=1,4 and y(5) = T) and yprime is the array that contains the derivatives of the solution components at t.
The program solves the system from t to tout and it is easy to continue the solution to get results at additional tout. In our case, we are going to get results at different values of X, between 0 and 1.
This problem is rather complex because most of the other variables depend on yi: the kinetic, adsorption and thermodynamic equilibrium “constants” depend on T (y5), the reaction rate and the components rate of formation depend on yi (fi (i=1,4) and T), as the activity coefficients.
In Figure 2 is the algorithm to solve our problem.
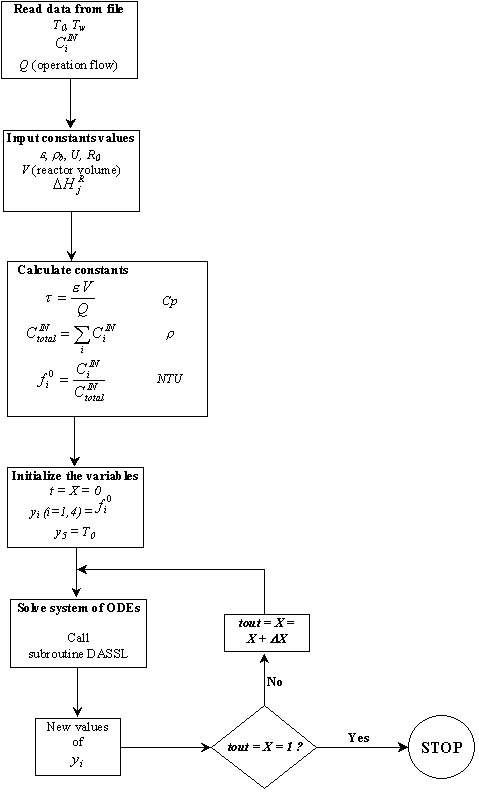
Fig. 2: Algorithm to solve the problem.
Some results
For both cases, isothermal and non-isothermal, the feed concentrations were the same:
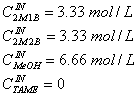
These concentrations lead to a feed mole ratio MeOH/isoamylenes, RM/IA, of 1.0.
a) Figures R.1, R.2 and R.3 represent the concentration profiles for a 10 m3 isothermal PFR, operating at 323 K, 343 K and 363 K, and a flow of 40 L/min.
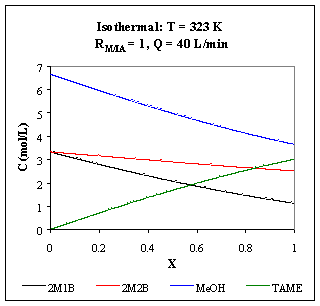 |
Fig. R.1: Concentration profiles for a 10 m3 isothermal PFR operating at 323 K.
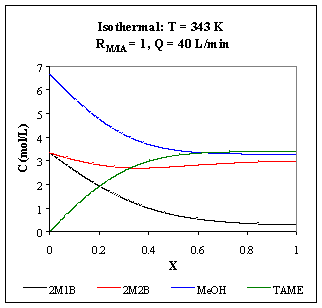
Fig. R.2: Concentration profiles for a 10 m3
isothermal PFR operating at 343 K.
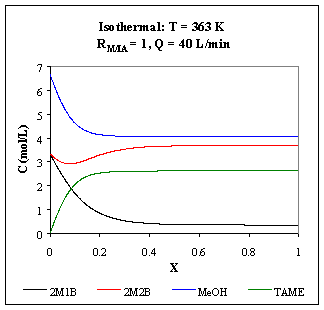
Fig. R.3: Concentration profiles for a 10 m3
isothermal PFR operating at 363 K
As the temperature increases, the reactions are faster, favoring TAME production, but the chemical equilibrium is moved to the opposite direction: for an operating temperature of 363 K, the equilibrium concentration of TAME is reached faster than for 343 K, but its value is lower.
b) Figure R.4 represents the exit concentrations as a function of the entering temperature, T0, for a 10 m3 isothermal PFR operating with a flow of 40 L/min.
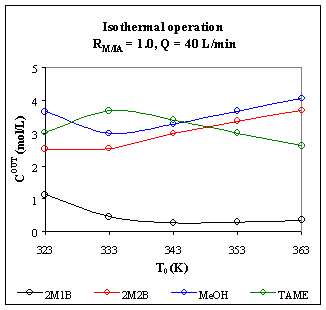
Fig. R.4: Exit concentrations as function of T0,
for a 10 m3 isothermal PFR
Figure R.4 shows that there is an optimum operating temperature around 333 K that leads to a maximum exit concentration for TAME. It is due to the fact that we have a system with competition between kinetics and equilibrium, as we are going to see for the non-isothermal PFR
c) We chose a reactor diameter of 1 m (for a volume of 10 m3 it leads to a reactor length of 12.7 m approximately) and for the wall temperature, we decided to use room temperature: 298 K. The entering temperature is 353 K.
It is important to notice that the catalyst used in TAME production is a macroreticular strong cation ion-exchange resin in hydrogen form (Amberlyst 15 Wet, Rohm & Haas) that has a maximum operating temperature of 393 K.
Figure R.5 represents the concentration (a) and temperature (b) profiles for an operating flow of 200 L/min.
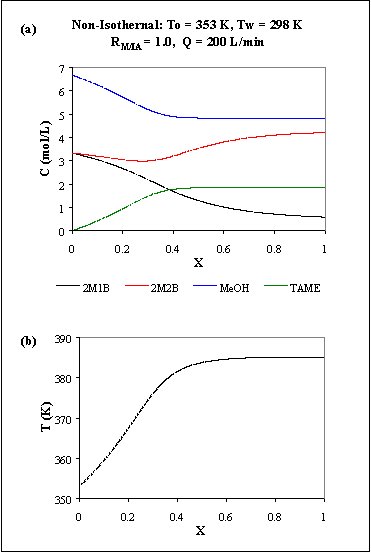
Fig. R.5: Non-isothermal PFR: (a) concentration profiles; (b) temperature profile.
Figure R.5(a) shows the competition between the three reactions: first, 2M1B and 2M2B react with MeOH to produce TAME and the reactants concentrations decrease and TAME concentration increases; but then, although MeOH and TAME concentrations are almost constant, 2M1B is still decreasing and 2M2B starts to increase: the third reaction, the isomerization, is now more evident.
The temperature profile (Fig. R.5(b)) shows that the reactor seams to be almost adiabatic (no heat losses through the reactor walls) since the reactor temperature is always increasing. This close to adiabatic behavior was expected since the reactor diameter is rather large: 1 m. But the temperature reaches a value that is very close to the catalyst limit: remember that its maximum operating temperature is 393 K and the reactor is reaching 385 K.
To see what is the maximum temperature that the reactor reaches, we can make it adiabatic setting the overall heat-transfer coefficient equal to zero: U = 0. In Figure R.6 are the results for the adiabatic reactor.
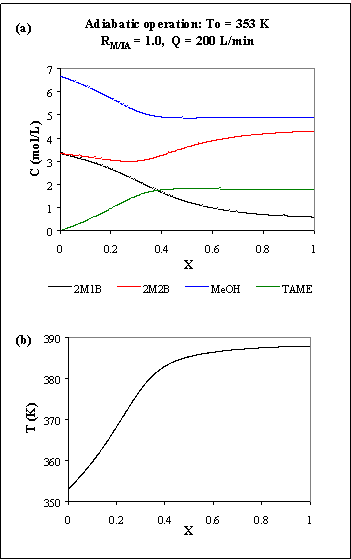
Fig. R.6: Adiabatic PFR: (a) concentration profiles; (b) temperature profile.
The maximum temperature reached by the reactor is 388 K. Comparing Figures R.5 and R.6 it is easy to see that the non-isothermal 1m diameter PFR can be considered adiabatic: the concentration and temperature profiles are almost the same.
To improve the reactor production, i.e., to reach higher exit concentrations of TAME, we can use a multi-tubular reactor. Lets think of a reactor composed of 4000 tubes (each one considered as a PFR) with a diameter of 1’’ each. To have a total reactor volume of 10 m3, each tube has a length of 5 m. In order to compare the results of the multi-tubular reactor with the ones obtained with the 1 m diameter PFR (Fig. R.5), we have to choose similar operating conditions: to have a total operating flow of 200 L/min, the equivalent flow in each tube is 0.05 L/min; since the reactor is now really cooled, we will choose the “best” temperature for the cooling fluid (333 K, as seen with the isothermal behavior runs). Figure R.7 shows the results for one of this tubes operating in the above conditions.
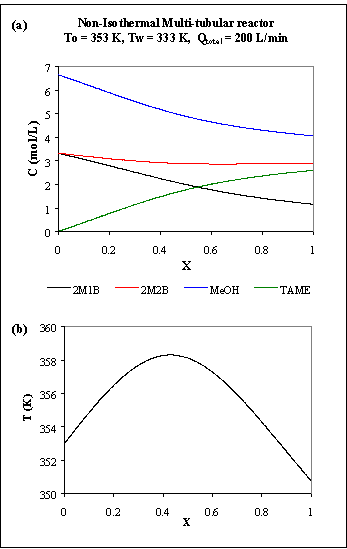
Fig. R.7: Multi-tubular reactor: (a) concentration profiles; (b) temperature profile.
The maximum temperature reached is 358 K - in this case there are no problems with the catalyst - and the exit concentration of TAME is higher: 2.603 mol/L against 1.862 mol/L for the PFR in Figure R.5, which represents an increase of 28.5 %.
References
Brenan, K., Campbell, S. and L. Petzold, “Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations, Elsevier, N.Y. (1989).
Kitchaiya, P. and R. Datta, “Ethers from Ethanol. 2. Reaction Equilibria of Simultaneous tert-amyl Ethyl Ether Synthesis and Isoamylene Isomerization”, Ind. Eng. Chem. Res. 34 (1995) 1092-1101.
Kiviranta-Pääkkönen, P.K., Struckman, L.K. and A.O.I. Krause, “Comparison of the Various Kinetic Models of TAME Formation by Simulation and Parameter Estimation”, Chem. Eng. Technol. 21 (1998) 321-326.
Oktar, N., Mürtezaoglu, K., Dogu, T. and Gülsen Dogu, “Dynamic Analysis of Adsorption Equilibrium and Rate Parameters of Reactants and Products in MTBE, ETBE and TAME Production”, Can.J. Chem. Eng. 77 (1999) 406-412.
Perry, R.H. and Dan W. Green, “Perry’s Chemical Engineers’ Handbook”, 7th edition, McGraw-Hill (1997).
Reid, R.C., Prausnitz, J.M. and Thomas K. Sherwood, “The Properties of Gases and Liquids”, 3rd edition, McGraw-Hill (1977).
Reid, R.C., Prausnitz, J.M. and B.E. Poling, “The Properties of Gases and Liquids”, 4th edition, McGraw-Hill (1987).
Vilarinho Ferreira, M.M. and J.M. Loureiro, “Synthesis of TAME: Kinetics in Batch Reactor and Thermodynamic Study”, presented on the “3rd European Congress of Chemical Engineering, ECCE3”, Nuremberg, Germany (June 2001).
Zhang, T. and R. Datta, “Integral Analysis of Methyl tert-Butyl Ether Synthesis Kinetics”, Ind. Eng. Chem. Res. 34 (1995) 730-740.