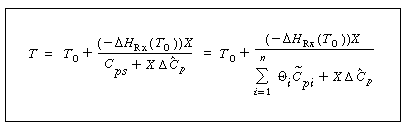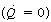Professional Reference Shelf

R9.5 Adiabatic Operation of Batch Reactors

		For adiabatic operationand when the work done by the stirrer can be neglected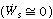Equation (9-12) can be written as
			(9-13)
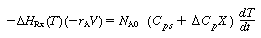
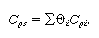		whereAn analytical solution relating X and T can be found for the case of constant or mean heat capacity. Combining Equations (2-6) and (9-13) yields
			(9-15)
		multiplying by dt, separating variables and integrating between the initial conditions, X = 0 and T =T0, and later conditions X =X and T =T, yields
		Taking the antilog, we have
		solving for X yields
		Then
			(9-16)
		This form is the same as the equation relating X and T derived for flow reactors. Rearranging yields
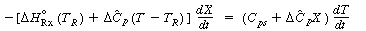
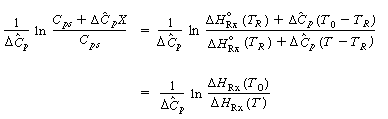
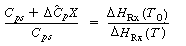
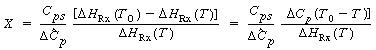
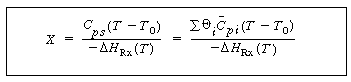
Temperature conversion relationship for an adiabatic batch reactor			(9-17)