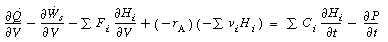We plan to reduce the energy balance into a more usable
form. To achieve this form for plug-flow
reactors, we begin by applying the balance to a small differential volume,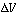 ,
in which there are no spatial variations (Figure R9.6-1). The number of moles
of species i in
,
in which there are no spatial variations (Figure R9.6-1). The number of moles
of species i in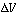 is
is
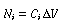
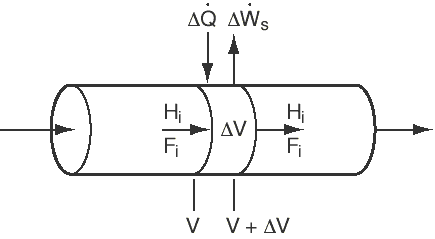
Figure CD9-6
PFR with heat gain or loss.
Substituting for Ni
in Equation (9-3) and dividing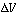 by
gives
by
gives
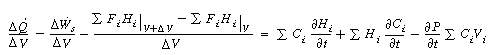
Taking the limit as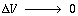 and
noting that gives
and
noting that gives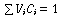
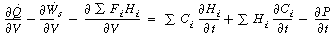
Rearranging, we have
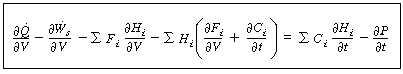
(R9.6-1)
Comparing Equations (R9.6-1) and (9-26)
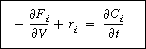
(R9.6-2)
we note that the term in parentheses is just ri.
The rate of reaction of species i is related to the rate of disappearance
of species A through the stoichiometric coefficient, 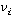
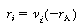
Then
|
|
Finally,
To include radial variations in temperature, see Problem P8-29
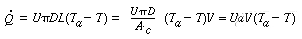
where a is the heat exchange area per unit volume. Differentiating yields
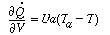
Recalling that
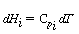
we substitute these equations into Equation (9-22) to obtain
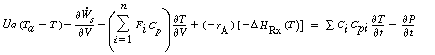
Neglecting shaft work and changes in pressure with respect to time, we obtain
Transient energy
balance on a PFR
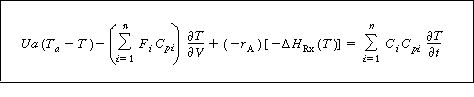
(R9.6-3)
This equation must be coupled with the mole balances,
(R9.6-4)
Numerical solution
required for these
three coupled
equations
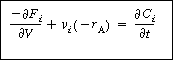
and the rate law,
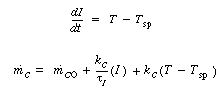
(R9.6-5)
and solved numerically. A variety of numerical techniques
for solving equations of this type can be found in the book Applied Numerical
Methods.1
We note, however, one can approximate the partial differential equation (PDE) of the unsteady PFR energy balance by replacing the PFR with a number of CSTRs in series. One then simply solves the coupled ODEs using Polymath™ or MATLAB™.
For steady-state operation in which no work is done by the system, Equation (R9.6-3) reduces to
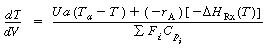
(8-60)
Substitution for the molar flow rates Fi in terms of conversion gives Equation (8-56).
Use this
equation for
steady-state
energy balance
on a PFR
with heat transfer
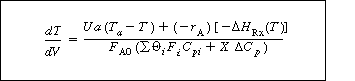
(8-56)
As stated previously, this equation is solved simultaneously with the mole balance.