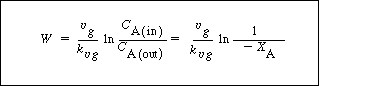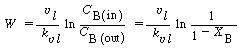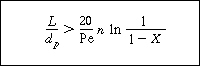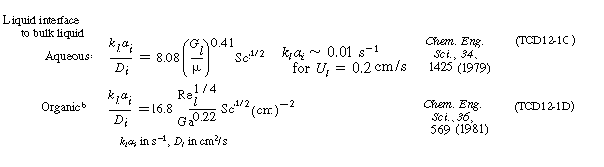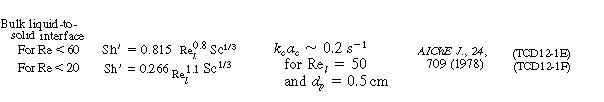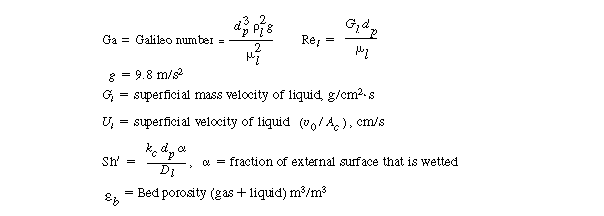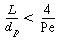|
|
|
|
|
|
Characteristics
and uses of a
trickle bed
reactor
|
|
In a trickle bed reactor the gas and liquid flow (trickle) concurrently downward
over a packed bed of catalyst particles. Industrial trickle beds are typically 3
to 6 m deep and up to 3 m in diameter and are filled with catalyst particles ranging
from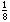 to to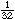 in. in diameter. The
pores of the catalyst are filled with liquid. In petroleum refining, pressures of
34 to 100 atm and temperatures of 350° to 425°C are not uncommon. A pilot-plant
trickle bed reactor might be about 1 m deep and 4 cm in diameter. Trickle beds are
used in such processes as the hydrodesulfurization of heavy oil stocks, the hydrotreating
of lubricating oils, and reactions such as the production of butynediol from acetylene
and aqueous formaldehyde over a copper acetylide catalyst. It is on this latter type
of reaction, in. in diameter. The
pores of the catalyst are filled with liquid. In petroleum refining, pressures of
34 to 100 atm and temperatures of 350° to 425°C are not uncommon. A pilot-plant
trickle bed reactor might be about 1 m deep and 4 cm in diameter. Trickle beds are
used in such processes as the hydrodesulfurization of heavy oil stocks, the hydrotreating
of lubricating oils, and reactions such as the production of butynediol from acetylene
and aqueous formaldehyde over a copper acetylide catalyst. It is on this latter type
of reaction,
|
|
|
|
|
|
|
|
|
|
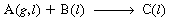
|
(R12.2-1)
|
|
|
|
|
|
|
|
|
that we focus in this section. In a few cases, such as the Fischer-Tropsch
synthesis, the liquid is inert and acts as a heat transfer medium.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The basic reaction and transport steps in trickle bed reactors are
similar to slurry reactors. The main differences are the correlations used to determine
the mass transfer coefficients. In addition, if there is more than one component
in the gas phase (e.g., liquid has a high vapor pressure or one of the entering gases
is inert), there is one additional transport step in the gas phase. Figure R12.2-1
shows the various transport steps in trickle bed reactors. Following our analysis
for slurry reactors we develop the equations for the rate of transport of each step.
|
|
|
|
|
|
|
|
|
|
1. Transport from the bulk gas phase to the gas-liquid interface.
The rate of transport per mass of catalyst is
|
|
|
|
|
|
|
|
|
|
|
|
|
Transport from bulk
gas to gas-liquid
interface to
bulk liquid
to solid-liquid
interface
Diffusion and
reaction in
catalyst pellet
|
|
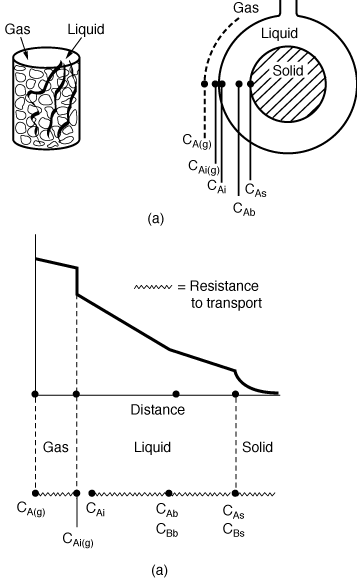
Figure R12.2-1
(a) Trickle bed reactor; (b) reactant concentration profile.
|
|
|
|
|
2. Equilibrium at gas-liquid interface:
|
|
|
|
|
|
|
|
|
|
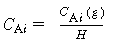
|
(R12.2-3)
|
|
|
|
|
|
|
|
|
C Ai = concentration of
A in liquid at the interface
H = Henry's constant
|
|
|
|
|
|
|
|
|
|
3. Transport from interface to bulk liquid:
|
|
|
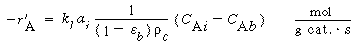
|
(R12.2-4)
|
|
|
|
where
|
|
|
|
|
k 1
= liquid-phase mass transfer coefficient, m/s
C Ai = concentration
of A in liquid at the interface, kmol/m 3
C Ab = bulk liquid concentration of A,
kmol/m 3
|
|
|
|
|
|
|
|
|
|
4. Transport from bulk liquid to external catalyst surface:
|
|
|
|
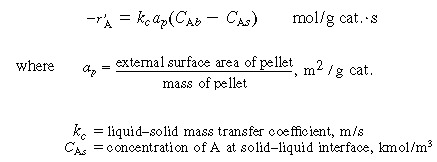
|
(R12.2-5)
|
|
|
|
|
|
|
|
|
5. Diffusion and reaction in the pellet. If we assume a first-order
reaction in dissolved gas A and in liquid B, we have
|
|
|
|
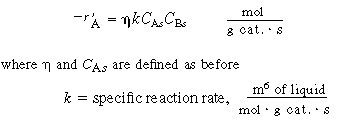
|
(R12.2-6)
|
|
|
|
|
|
|
|
|
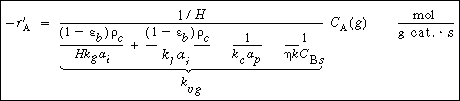
Combining Equations (R12.2-2) through (R12.2-6) and rearranging in a
manner identical to that leading to the development of Equation (12-89) for slurry
reactors, we have
|
|
|
|
|
|
|
|
The overall rate equation for A
|
|
(R12.2-7)
|
|
|
|
|
|
|
|
|
that is,
|
|
|
|
|
|
|
|
|
|
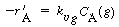
|
(R12.2-8)
|
|
|
|
|
|
|
|
|
where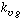 is the overall transfer coefficient for the gas into
the pellet (m 3 of gas/g cat. is the overall transfer coefficient for the gas into
the pellet (m 3 of gas/g cat. s). A mole balance on species A gives s). A mole balance on species A gives
|
|
|
|
|
|
|
|
|
|
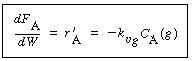
|
(R12.2-9)
|
|
|
|
|
|
|
|
|
We next consider the transport and reaction of species B, which does
not leave the liquid phase.
|
|
|
|
|
|
|
|
|
|
6. Transport of B from bulk liquid to solid catalyst interface:
|
|
|
|
|
|
|
|
|
|
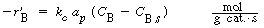
|
(R12.2-10)
|
|
|
|
|
|
|
|
|
where C B and
C Bs are the concentrations
of B in the bulk fluid and at the solid interface, respectively.
|
|
|
|
|
|
|
|
|
|
7. Diffusion and reaction of B inside the catalyst pellet:
|
|
|
|
|
|
|
|
|
|
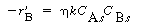
|
(R12.2-11)
|
|
|
|
|
|
|
|
|
Combining Equations (12-33) and (12-34) and rearranging, we have
|
|
|
|
|
|
|
|
The overall rate
equation for B
|
|
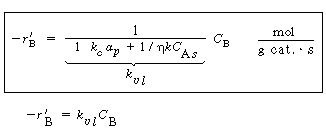
|
(R12.2-12)
|
|
|
|
|
|
|
|
|
A mole balance on species B gives
|
|
|
|
|
|
|
|
Mole balance on B
|
|
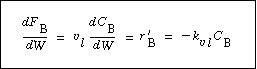
|
(R12.2-13)
|
|
|
|
|
|
|
|
|
One notes that the surface concentrations of A and B, CAs and C B
s , appear in the denominator of the overall transport
coefficients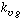 and and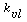 . .
|
|
|
|
|
Consequently, Equations (R12.2-7), (R12.2-9), (R12.2-12), and (R12.2-13)
must be solved simultaneously. In some cases analytical solutions are available,
but for complex rate laws, one resorts to numerical solutions. 1 However, we shall
consider some limiting situations.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mass Transfer of the Gaseous Reactant Limiting. For this situation
we assume that either the first three terms in the denominator of Equation (R12.2-7)
are dominant or that the liquid-phase concentration of species B does not vary significantly
through the trickle bed. For these conditions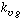
|
|
|
|
|
is constant and we can integrate the mole balance. For negligible
volume change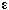 = 0, then = 0, then
|
|
|
|
|
|
|
|
Catalyst weight
necessary to achieve a conversion
X A of gas-phase reactant
|
|
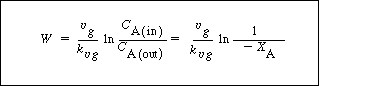
|
(R12.2-14)
|
|
|
|
|
|
|
|
|
Mass Transfer and Reaction of Liquid Species Limiting. Here
we assume that the liquid phase is entirely saturated with gas throughout the column.
As a result, C As is a constant.
Consequently, we can integrate the combined mole balance and rate law to give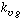 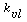 . .
|
|
|
Catalyst weight
necessary to achieve
a conversion
X B of gas-phase reactant
|
|
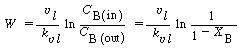
|
(R12.2-15)
|
|
|
|
|
|
|
|
|
The mass transfer coefficients, k g
,
k l , and k
c depend on a number of variables, such as type of packing, flow rates, wetting of
particle, and geometry of the column, and as a result the correlations vary significantly
from system to system. Consequently, we will not give all the correlations here but
instead will give correlations for particular systems and refer the reader to four
specific references where other correlations for trickle bed reactors may be found. 2
Typical correlations are given in Table R12.2-1. Note that the correlation for organic
particles tends to under predict the transport coefficient.
|
|
|
|
|
|
|
|
Criterion for assuming
that plug flow
is valid
|
|
The representative correlations given in Table R12.2-1 assume complete
wetting of the catalyst particles. Corrections for incomplete wetting as flow regimes,
pressure-drop equations, and other mass transfer correlations can be found in the
reviews by Shah, Smith, and Satterfield.
3
The plug-flow design equation may be applied successfully provided that the ratio
of reactor length L to particle diameter d p
satisfies the criterion (Satterfield, 1975)
|
|
|
|
|
|
|
|
|
|
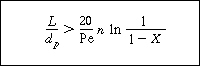
|
(R12.2-16)
|
|
|
|
where
Pe = Péclet number = d p U
l /D AX
D AX = axial dispersion
coefficient
n = reaction order
|
|
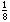 to
to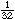 in. in diameter. The
pores of the catalyst are filled with liquid. In petroleum refining, pressures of
34 to 100 atm and temperatures of 350° to 425°C are not uncommon. A pilot-plant
trickle bed reactor might be about 1 m deep and 4 cm in diameter. Trickle beds are
used in such processes as the hydrodesulfurization of heavy oil stocks, the hydrotreating
of lubricating oils, and reactions such as the production of butynediol from acetylene
and aqueous formaldehyde over a copper acetylide catalyst. It is on this latter type
of reaction,
in. in diameter. The
pores of the catalyst are filled with liquid. In petroleum refining, pressures of
34 to 100 atm and temperatures of 350° to 425°C are not uncommon. A pilot-plant
trickle bed reactor might be about 1 m deep and 4 cm in diameter. Trickle beds are
used in such processes as the hydrodesulfurization of heavy oil stocks, the hydrotreating
of lubricating oils, and reactions such as the production of butynediol from acetylene
and aqueous formaldehyde over a copper acetylide catalyst. It is on this latter type
of reaction,
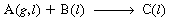
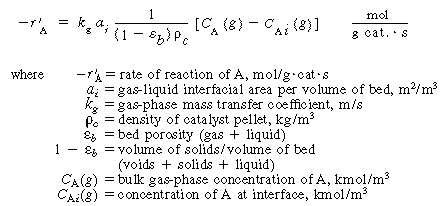

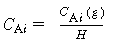
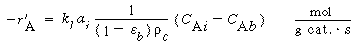
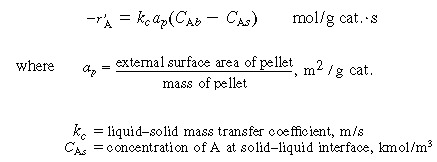
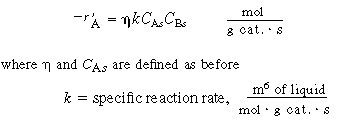

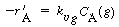
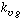 is the overall transfer coefficient for the gas into
the pellet (m 3 of gas/g cat.
is the overall transfer coefficient for the gas into
the pellet (m 3 of gas/g cat. s). A mole balance on species A gives
s). A mole balance on species A gives
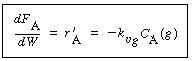
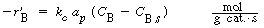
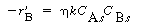
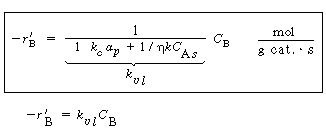
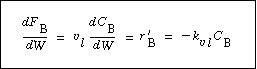
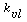 .
.
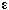 = 0, then
= 0, then