 .
.
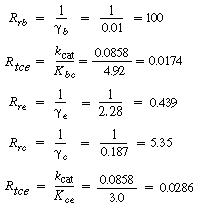
|
Electrical |
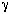 e .
e .
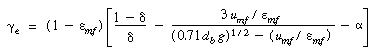
(CD12-80)

Figure CD12-11
Electrical Analog
Calculate each of the resistances to reaction and transfer and the
relationship between C Ab , C Ac
, and C Ae for
the ammonia oxidation reaction described in Example CD12-2. Assume that  . .
|
||||
| Solution | ||||
|
|
||||
| To relate C Ae and C Ac we rearrange Equation (CD12-67) for a first-order reaction as | ||||
|
|
||||
|
|
||||
|
The analog electrical resistance for the system is shown in Figure
CD12-11 along with the corresponding resistances for this reaction. As with its electrical
analog, the reaction will pursue the path of least resistance, which in this case
is along the right-hand-side branch of Figure CD12-11. If the major resistance in
this side, the resistance to reaction in the emulsion R re , could be reduced, a greater conversion could be achieved for a specific
catalyst weight. To reduce R re one needs to look for ways of increasing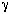 e . e .
|
|||
|
|
(CD12-80) |
|||
|
Figure CD12-11 |
||||
Examination of Equation (CD12-80) shows that decreasing the bubble
fraction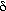 and the minimum fluidization velocity would increase and the minimum fluidization velocity would increase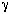 e and hence the conversion. The
minimum fluidization velocity could be decreased by decreasing the particle size.
We will investigate how the various parameters will affect the conversion for different
limiting situations. e and hence the conversion. The
minimum fluidization velocity could be decreased by decreasing the particle size.
We will investigate how the various parameters will affect the conversion for different
limiting situations.
|