Professional Reference Shelf

Example CD12-8: Diffusion Between Wafers

    Derive an equation for the reactant gas concentration as a function of wafer radius and then determine the effectiveness factor.  
       
   

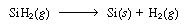
image 12eq265.gif

 
       
    In terms of the diffusing gas phase components, we can write this reaction as  
       
   

image v

 
       
    Solution
The shell balance on the reactant diffusing between two wafers separated by a distance l shown in Figure CDE12-9.1 gives 		 
       
   

 
       
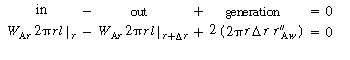
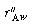    where is the rate of generation of species A per unit wafer surface area. The factor of 2 appears in the generation term because there are two wafer surfaces exposed in each differential volume element. Dividing by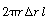, taking the limit as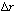approaches zero, and then rearranging gives  
       
   

(CDE12-9.1)
    Recalling the constitutive equation for the molar flux W Ar in radial coordinates yields  
   

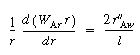
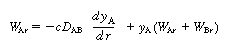
image 12eq272.gif

(CDE12-9.2)
       

Diffusion between
the wafers

 

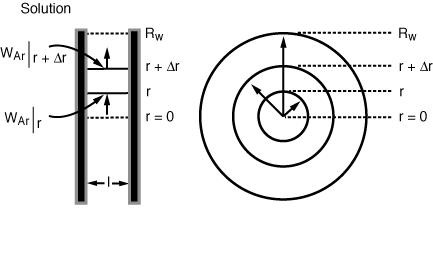
Figure 12-9-1

 
       
    For every one molecule of SiH 2 (i.e., species A) that diffuses in, one molecule of H 2 (i.e., species B) diffuses out.  
       
   

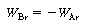
image 12eq273.gif

 
    Then  
       
   

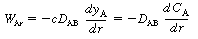
image 12eq274.gif

(CDE12-9.3)
       
    For a first-order reaction,  
       
   

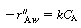
image 12eq275.gif

(CD12-101)
       
       
    Substituting Equations (CD12-20) and (CDE12-2.3) into Equation (CDE12-2.1), we get  
       

Diffusion with
reaction between
wafers

 

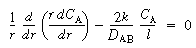
image 12eq276.gif

(CDE12-9.4)
       
    The corresponding boundary conditions are  
   

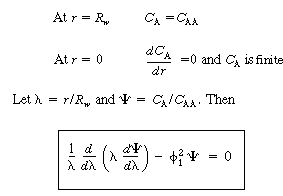
image12eq277.gif


(CDE12-9.5)


(CDE12-9.6)






(CDE12-9.7)
       
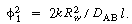    where image 12eq278.gif The boundary conditions are  
       
   

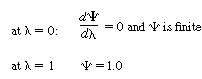
image 12eq279.gif

 
       
    Equation (CDE12-9.2) is a form of Bessel's equation. The general form of the solution to Bessel's equation is 28  
       
   

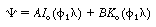
image 12eq280.gif

(CDE12-9.8)
       
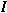    whereimage Cap i.gifo is a modified Bessel function of the first kind of order zero and K o is a modified Bessel function of the second kind of order zero. The second boundary condition requires 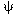to be finite at 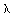= 0. Therefore, B must be zero because K o (0) =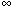. Using the first boundary condition, we get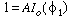; then 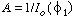. The concentration profile in the space between the wafers is  
       

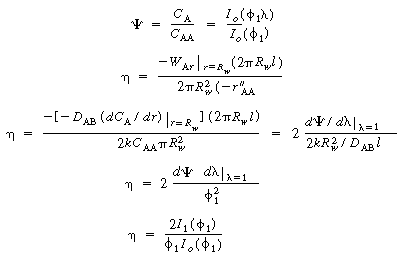
image 12eq283.gif



(CDE12-9.9)


(CDE12-8.10)




(CDE12-9.11)




(CDE12-9.12)
       
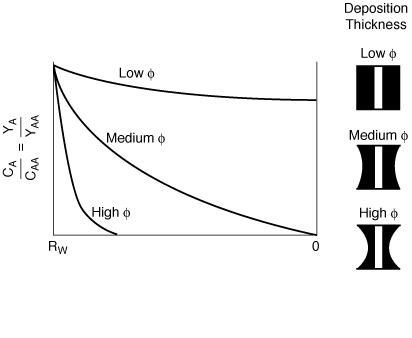
    The concentration profile along the radius of the wafer disk and the wafer shape are shown in Figure CDE12-9.2 for different values of the Thiele modulus.  
       
       
   

Figure CD12-9-2
Radial concentration profile