Solved Problems - Chapter 13

Learning Resources

Consider the reaction



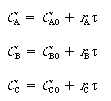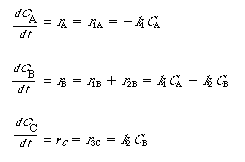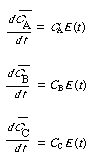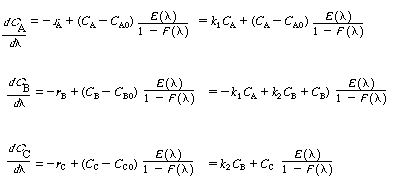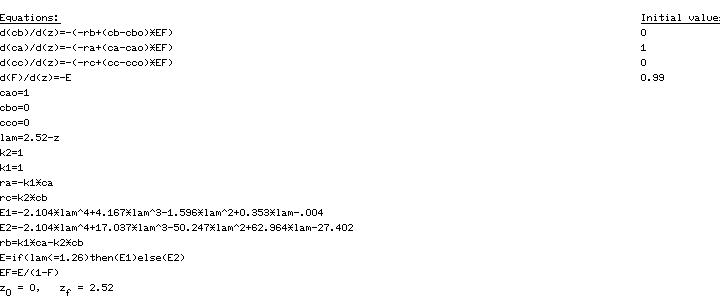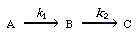
occurring in two different reactors with the same mean residence time t_m=1.26 min, but with the following residence-time distributions which are quite different: (a) Calculate the conversion predicted by an ideal PFR. CSTR. (b) Fit a polynomial to each RTD (Figures CDE13-1.1 and CDE13-1.2). Note: These curves are identical to Figures E13-9.1 and E13-9.2 in the text.

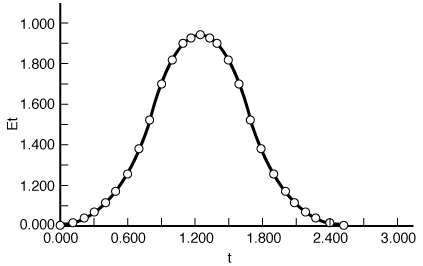
Figure CDE13-1.1 E₁ (t ):asymmetric distribution.

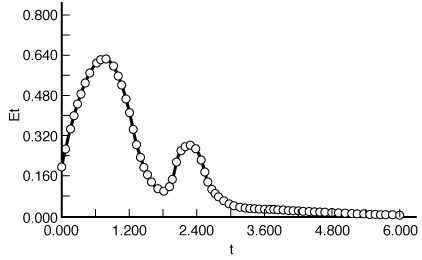
Figure CDE13-1.2 E₂ (t ): bimodal distribution.
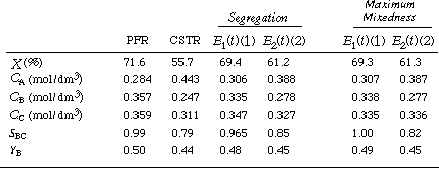
(c) For the multiple reaction sequence given above, determine the product distribution in each reactor for 1. The segregation model. 2. The maximum mixedness model.
Solution PFR Combining the mole balance and rate laws for a PFR reactor, we have

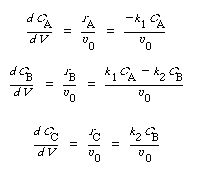
	(CDE13-1.1) (CDE13-1.2) (CDE13-1.3)
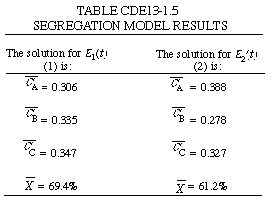
The initial conditions are V = 0, C_A = 1, C_B = C_C = 0. In order to compare the performance of the different models and different RTDs, the mean residence time,, was set equal to 1.26 min. The POLYMATH program used to solve this PFR system is shown in Table CDE13-1.1. The solution is C_A = 0.284, C_B = 0.357, C_C = 0.359, X = 71.6%.

Table CDE13-1.1.
Polymath Program for Reactions in a Series in a PFR


CSTR The mole balances on A, B, and C for a CSTR are

	(CDE13-1.4) (CDE13-1.5) (CDE13-1.6)

The equations can be solved with a nonlinear equation solver. Again,was set to 1.26 min for comparison reasons.

The POLYMATH program for the CSTR model is shown in Table CDE13-1.2.The solution is C_A = 0.443, C_B = 0.247, C_C = 0.311, X = 55.7%

Table CDE13-1.2.
Polymath Program for Reactions in a Series In a CSTR


Segregation Model Combining the mole balance and rate laws for a constant-volume batch reactor, we have: For the globules

	(CDE13-1.7) (CDE13-1.8) (CDE13-1.9)
For the exit concentrations

	(CDE13-1.10) (CDE13-1.11) (CDE13-1.12)

The initial conditions are t = 0, C_A= 1, C_B = C_C = 0 The POLYMATH program used to solve these equations is shown in Table CDE13-1.3 forE₁(t) (1) and in Table CDE13-1.4 for E₂(t) (2).The results are listed in Table CDE13-1.5.

Table CDE13-1.3.
POLYMATH Program for Segregation Model with Asymmetric RTD

Table CDE13-1.4.
POLYMATH Program for Segregation Model with Bimodal Distribution





Maximum Mixedness Model The equations describing the variations in concentrations with position (life expectancy) are

	(CDE13-1.13) (CDE13-1.14) (CDE13-1.15)
The POLYMATH program is shown in Table CDE13-1.6 for E₁(t) (1)and in Table CDE13-1.7 for (2). The results are listed in Table CDE13-1.8.

Table CDE13-1.6.
POLYMATH Program for Maximum Mixedness Model with Asymmetric RTD

Table CDE13-1.7.
POLYMATH Program for Maximum Mixedness Model with Bimodal Distribution




Summary: Example CD13-1



Additional Tables for Example 13-9 Table CDE13-9.5. POLYMATH Program for Segregation Model with Bimodal Distribution (Multiple Reactions) Table CDE13-9.6 POLYMATH Program for Maximum Mixedness Model with Asymmetric RTD (Multiple Reactions)