| Select Chapter >> | TOC | Preface | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | Appendices |
Chapter 3: Rate Laws
Collision Theory
Derivation for model 2
The impact parameter, b, is the off-set distance of the centers as they approach one another. The velocity component along the lines of centers, ULC, can be obtained by resolving the approach velocity into components.
At the point of collision the center of B is within the distance σ AB
The energy along the line of centers can be developed by a simple geometry arguments
 |
(1) | |
| The component of velocity along the line of centers | ||
ULC = UR cosΘ |
(2) | |
| The kinetic energy along the line of centers is | ||
 |
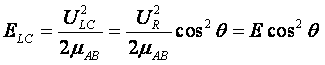(3) | |
 |
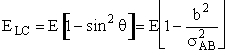(4) |
The minimum energy along the line of centers necessary for a reaction to take place, EA, corresponds to a critical value of the impact parameter, bcrit. In fact, this is a way of defining the impact parameter and corresponding reaction cross section
 |
(5) | |
| Substituting for EA and bcrit in Equation (4). | ||
 |
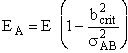(6) | |
Solving for  |
||
 |
(7) | |
| The reaction cross section for energies of approach E > EA, is | ||
 |
(8) | |
| The complete reaction cross section for all energies E is | ||
 |
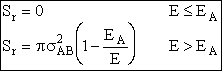(9) (10) |