Chapter 3: Rate Laws
Transition State Theory
Derivation of Transitional Partition Function q'T
To show
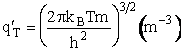 |
(T1) |
Translational Energy
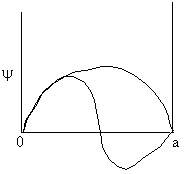
We solve the Schrödinger equation for the energy of a molecule trapped in an infinite potential well. This situation is called "a particle in a box". For a particle in a box of length a
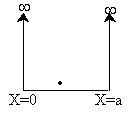
The potential energy is zero everywhere except at the walls where it is infinite so that the particle cannot escape the box. Inside the box
| (T2) | ||
| The box is a square well potential where the potential is zero between x = 0 and x = a but infinite at x = 0 and x = a (A5p392). The solution is to the above equation is | ||
| (T3) | ||
| (T4) | ||
| where | ||
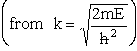 |
We now use the boundary conditions
Ψ = 0, sin 0 = 0, and cos 0=1 ∴ B = 0 The wave equation is now Ψ = A sin kx At x = a, Ψ = 0 Ψ will be zero provided ∴ ka = nπ where n is an integer, 1, 2, 3
|
(T5) |
Substituting (T5) into (T4) we see that only certain energy states are allowed
| (T6) | ||
For particle in a a 3-D box of sides a, b, and c |
||
| Back to one dimension | ||
| Therefore relative to the lowest energy level n = 1, the energy is | ||
| (T7) | ||
| Then | ||
| (T8) | ||
| (T9) |