Chapter 3: Rate Laws

Transition State Theory

Derivation of the Rotational Partition Function qR

Rigid Rotation 23

To show

   (R1)

where    
= Rotational Constant
   (R2)
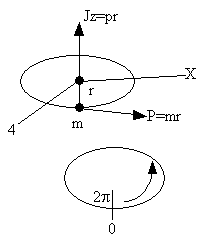
Consider a particle of mass m rotating about the z axis a distance r from the origin.    
  (R3)
   
This time we convert the wave equation to spherical coordinate to obtain 24    
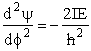  (R4)
Classical Energy of a rigid rotator is    
  (R5)
where w is the angular velocity (rod/s) and I is the moment of inertia 25    
  (R6)
where mi is the mass located and distance ri from the center of mass.    
Quantum mechanics solutions to the wave equation gives two quantum numbers, and m    
Magnitude of angular momentum =
   
z component of angular momentum = mh
    
  (R7)26
   
Let J ≡    
For a linear rigid rotator    
E = hcB J (J+ 1)
   (R8)
Where B is the rotation constant:    
  (R2)27
with    
c = speed of light
    
I = moment of inertia about the center of mass
    
The rotational partition function is    
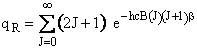  (R9)28
Replacing the by an integral from 0 to ∞ integrating, we obtain the rotational partition function qR for a linear molecule29    
This is the result we have been looking for!
  (R10)
where Sy is the symmetry number which is the number of different but equivalent arrangements that can be made by rotating the molecules.    

   
   
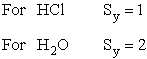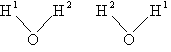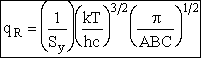where                      
Sy = symmetry number. 30 For a hetronuclear molecule σ= 1 and for a homonuclear diatomic molecule or a symmetrical linear molecule, e.g., H2, then σ= 2.    
Order of Magnitude and Representative Values    
   

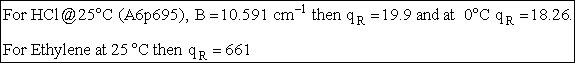23P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), pp. 409, 413, 557, A24.

24P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), p. 410.

25P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), p. 555.

26P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), pp. 408, 413.

27P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), p. 557.

28P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), pp. 414, 563, 671.

29 P. W. Atkins, Physical Chemistry, 5th ed. (New York: Freeman, 1994), p. 694.

30For discussion of s, see K. J. Laidler, Chemical Kinetics, 3rd ed. (New York: Harper Collins, 1987), p.99.

Return toTransition State Theory