Chapter 6: Isothermal Reactor Design: Molar Flow Rates
Professional Reference Shelf
The following information is taken from the 4th edition of Elements of Chemical Reaction Engineering, so the equation numbers correspond to those found in that bookStartup of a CSTR
The startup of a fixed volume CSTR under isothermal conditions is rare, but it does occur occasionally. We can, however, carry out an analysis to estimate the time necessary to reach steady-state operation. For the case when the reactor is well mixed and as a result there are no spatial variations in rA, we begin with the general mole balance equation applied to Figure 4-14(a):
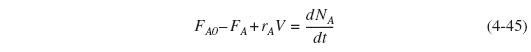
Conversion does not have any meaning in startup because one cannot separate
the moles reacted from the moles accumulated in the CSTR. Consequently, we
must
use concentration rather than conversion as our variable in the balance
equation. For liquid-phase ![]() reactions with constant overflow
reactions with constant overflow ![]() ,
using
,
using ![]() , we can transform Equation (4-45) to
, we can transform Equation (4-45) to
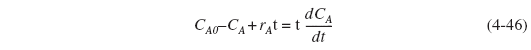
For a first-order reaction (-ra= k CA) Equation (4-46) then becomes
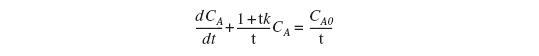
which, for the initial conditions CA= 0 at t = 0 solves to

Letting ts be the time necessary to reach 99% of the steady-state concentration, CAS:
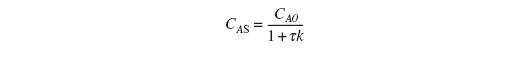
Rearranging Equation (4-47) ![]() for yields
for yields
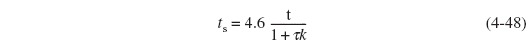
For slow reactions with small k(1 >>τk):
![]()
For rapid reactions with large k(τk>> 1):
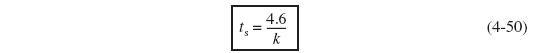
For most first-order systems, steady state is achieved in three to four space times.
Semibatch Reactors
Motivation
One of the best reasons to use semibatch reactors is to enhance selectivity in liquid-phase reactions. For example, consider the following two simultaneous reactions. One reaction produces the desired product D
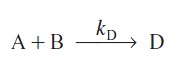
with the rate law
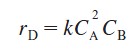
and the other produces an undesired product U
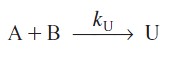
with the rate law
![]()
The instantaneous selectivity SD/U is the ratio of the relative rates

and guides us how to produce the most of our desired product and least of our undesired product (see Section 6.1). We see from the instantaneous selectivity that we can increase the formation of D and decrease the formation of U by keeping the concentration of A high and the concentration of B low. This result can be achieved through the use of the semibatch reactor, which is charged with pure A and to which B is fed slowly to A in the vat.
Of the two types of semibatch reactors, we focus attention primarily on the one with constant molar feed. A schematic diagram of this semibatch reactor is shown in Figure 4-15. We shall consider the elementary liquid-phase reaction
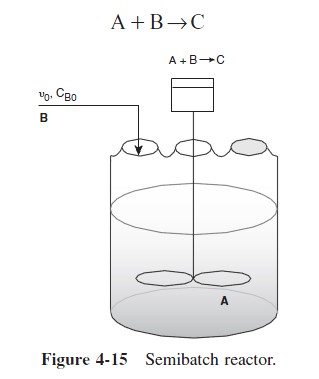
in which reactant B is slowly added to a well-mixed vat containing reactant A.
A mole balance on species A yields
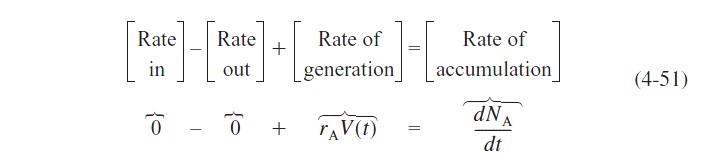
Three variables can be used to formulate and solve semibatch reactor problems: the concentrations, Cj, the number of moles, Nj, and the conversion, X.
Writing the Semibatch Reactor Equations in Terms of Number of Moles
Recalling that the number of moles of A, NA, is just the product of concentration of A, CA, and the volume, V, we can rewrite Equation (4-51) as

We note that since the reactor is being filled, the volume, V, varies with time. The reactor volume at any time t can be found from an overall mass balance of all species:
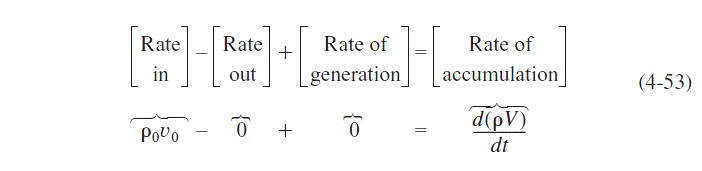
For a constant-density system, ρ=ρ0, and
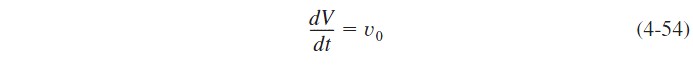
with the initial condition V= V0 at t=0, integrating for the case of constant volumetric flow rate v0 yields

Substituting Equation (4-54) into the right-hand side of Equation (4-52) and rearranging gives us

The balance on A [i.e., Equation (4-52)] can be rewritten as
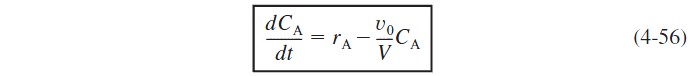
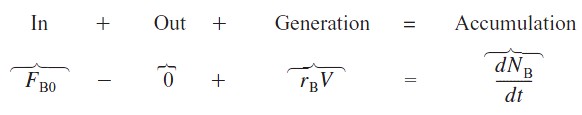
Rearranging

Substituting Equation (4-55) in terms of V and differentiating, the mole balance on B becomes
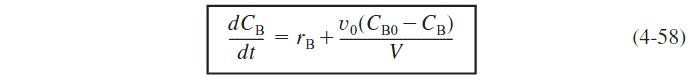
At time t = 0, the initial concentration of B in the vat is zero, CBi = 0. The concentration of B in the feed is CB0. If the reaction order is other than zero- or first-order, or if the reaction is nonisothermal, we must use numerical techniques to determine the conversion as a function of time. Equations (4-56) and (4-58) are easily solved with an ODE solver.


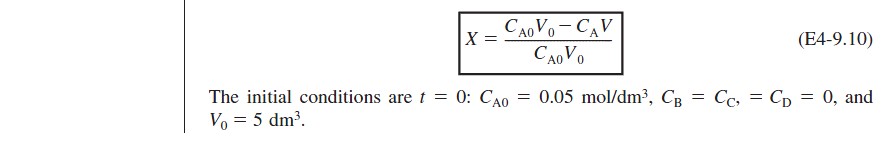
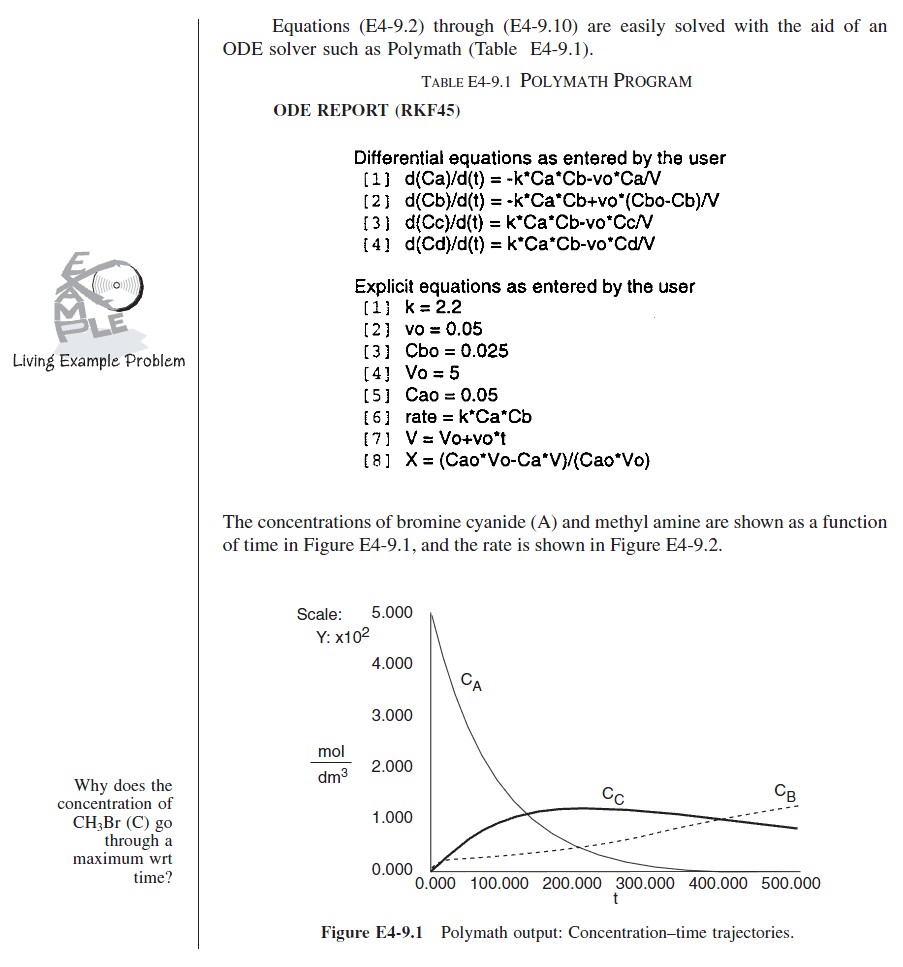
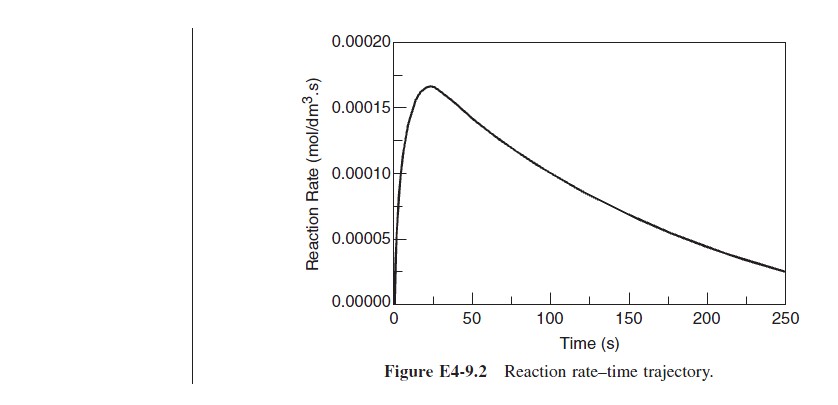
Writing the Semibatch Reactor Equations in Terms of Conversion
Consider the reaction
in which B is fed to a vat containing only A initially. The reaction is first-order in A and first-order in B. The number of moles of A remaining at any time, t, is
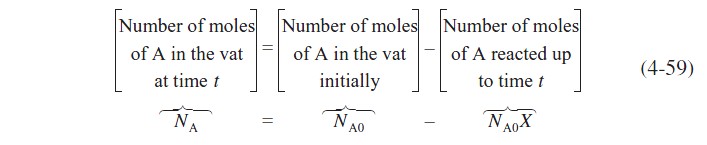
where X is the moles of A reacted per mole of A initially in the vat. Similarly, for species B,
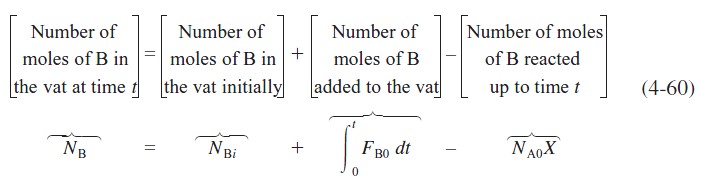
For a constant molar feed rate and no B initially in the vat,
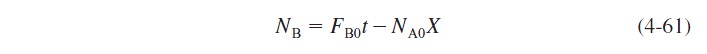
A mole balance on species A gives
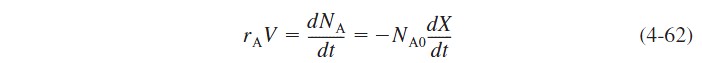
The number of moles of C and D can be taken directly from the stoichiometric table; for example,
For a reversible second-order reaction for which the rate law is
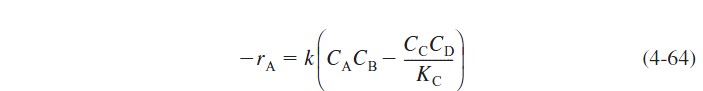
Recalling Equation (4-55), the concentrations of A, B, C, and D are
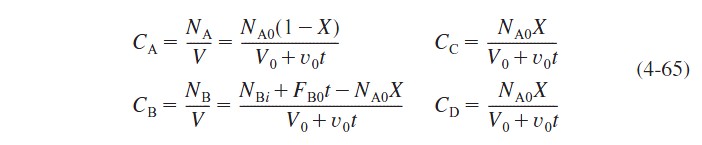
Combining equations (4-62), (4-64), and (4-65), substituting for the concentrations, and dividing by NA0, we obtain
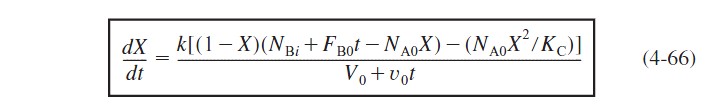
Equation (4-66) needs to be solved numerically to determine the conversion as a function of time.
The third variable, in addition to concentration and conversion, we can use to analyze semibatch reactors is the number of moles NA, NB, etc. This method is discussed in the Summary Notes on the CD-ROM.
Equilibrium Conversion
For reversible reactions carried out in a semibatch reactor, the maximum attainable conversion (i.e., the equilibrium conversion) will change as the reaction proceeds because more reactant is continuously added to the reactor. This addition shifts the equilibrium continually to the right toward more product.
If the reaction A + B ↔ C + D were allowed to reach equilibrium after feeding species B for a time t, the equilibrium conversion could be calculated as follows at equilibrium [see Appendix C]:
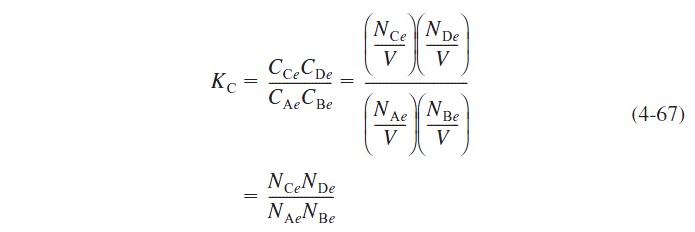
The relationship between conversion and number of moles of each species is the same as shown in Table 3-1 except for species B, for which the number of moles is given by Equation (4-61). Thus
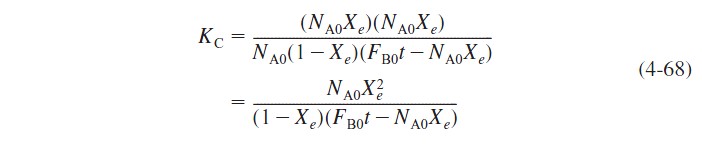
Rearranging yields
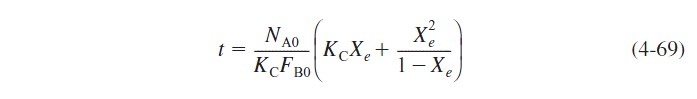
or
