![]()
|
|
Type 4 Home Problem
Problems that are under-specified and require the student to consult other information
sources.
PART 2 - Type 4 Solution
In Part 2, we must derive the equilibrium constant (KC) and the diffusion rate constant (kB). Often the exact value that is required is either too cumbersome to calculate or unavailable in the literature. Because we are just looking for estimates of KC and kB, several assumptions will be made. We will start with our derivation of KC.
We begin with a thermodynamic equation for KC:
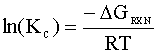
From Perry's Chemical Engineering Handbook 1, we find the following free energies of formation at 298 K for our components:
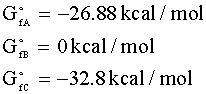
We then calculate the change in free energy for our reaction:
![]()
and insert the value into our KC equation:
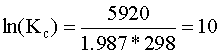
![]()
This value for KC favors our products.
Our next task is to calculate our diffusion rate constant (kB). To calculate it, we will need to introduce three new dimensionless constants--the Reynolds Number (Re), the Schmidt Number (Sc), and the Sherwood Number(Sh):
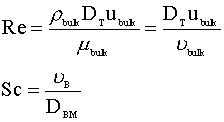
A correlation from Fundamentals of Momentum, Heat and Mass Transfer 2 by Welty, Wicks, and Wilson (or simply WWW), we can relate kB to Re and Sc through the Sherwood number (Sh):
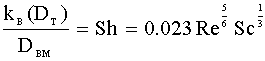
This equation is valid for 2000 < Re < 70000 and 1 < Sc < 2260.
First, we will approximate the bulk properties of our fluid by assuming that throughout the reactor, our fluid is half A and half C. From WWW, we found mC=1.785*10-5 kg /(m*s) (1 cP=0.1 Pa*s or kg/(m*s)), and from Perry's (Table 3-311), we found the viscosity of acetone. For the sake of these calculations we will assume that the viscosities of acetone and formaldehyde (A) are similar, mA=0.75*10-5 kg/(m*s).
![]()
The density of the bulk fluid will also be calculated using the 50-50% assumption:
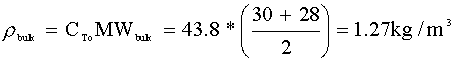
We need to calculate the superficial velocity of our fluid (ubulk). To do so we will assume the volumetric flow rate (vo) stays constant throughout the reactor:
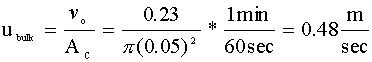
Now, we calculate Re:
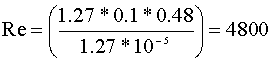
In order to determine Sc, we need to find the kinematic viscosity of the hydrogen (B). In WWW, we find that uB = 1.096*10-4 sec/m2. We then calculate the Schmidt number (Sh):
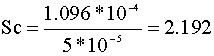
Using the Sherwood correlation, we solve for kB':
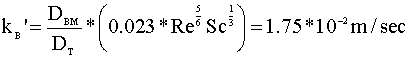
Unfortunately, kB' is the rate constant per membrane surface area. We need the diffusion rate constant (kB) per volume of the reactor. This conversion can be performed quite easily. We multiply by the perimeter and divide by the cross-sectional area:
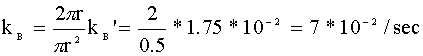
The diffusion rate constant per minute:
kB = 4.2/min
![]() Go to Part 3 of the Solution - Polymath
Go to Part 3 of the Solution - Polymath
![]() Back to PART 1 of the Solution
Back to PART 1 of the Solution
CRE Thoughts Ten Types Homogeneous Example 4
REFERENCES:
Perry, R.H. and Green, D.W. (Editors). Perry's Chemical Engineering Handbook, New York: MacGraw-Hill Inc., 1984.
Welty, J.R., Wicks, C.E., & Wilson, R.E. Fundamentals of Momentum, Heat and Mass Transfer, New York: Wiley & Sons, 1984.