Algorithm:
The basic algorithm for solving reaction engineering problems is described below. This algorithm is a useful tool, and it can be applied to a wide variety of reactor problems, not just membrane reactor problems.
For demonstration purposes, we'll examine a membrane reactor in which the following gas phase reaction occurs:
![]()
Product B diffuses through the membrane, but reactant A and product C do not.

1. Mole Balance:
For a differential mole balance on A in the catalytic bed at steady state:
IN (by flow) - OUT (by flow) + Generation = Accumulation
![]()
Dividing byand taking the limit as
gives:
![]()
Similarly, a differential mole balance on C in the catalytic bed at steady state will give:
IN (by flow) - OUT (by flow) + Generation = Accumulation
![]()
Dividing byand taking the limit as
gives:
![]()
The steady state, differential mole balance on B looks slightly different, since B is the only species that passes through the membrane:
IN (by flow) - OUT (by flow) + Generation - OUT (by diffusion) = Accumulation
![]()
where RB is the molar flowrate of B through the membrane per unit volume of the reactor.
Dividing byand taking the limit as
gives:
![]()
2. Rate Law:
The rate of disappearance of reactant A follows the rate law:
![]()
where k is the specific reaction rate constant, and KC is the equilibrium constant. Products B and C obey the following rate laws:
![]()
![]()
3. Transport Law:
The transport or flux of species B through the membrane follows the transport law:
![]()
where km is a mass transport coefficient for the flow of product B through the membrane.
4. Stoichiometry:
For gas-phase reactions:
![]()
The subscript o indicates initial conditions and v is the volumetric flow rate.
The concentrations, in terms of molar flow rates, are:
![]()
![]()
![]()
Substituting for the volumetric flow rate, we get:
![]()
![]()
![]()
If we make use of the fact that:
![]()
we can get our concentrations in terms of the total initial concentration:
![]()
![]()
![]()
Quite often we can make the assumption that the reactor operates isothermally and isobarically:
![]()
![]()
![]()
5. Combine:
Substituting the concentration terms into the rate law yields:
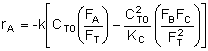
where the total molar flow rate is:
![]()
and:
![]()