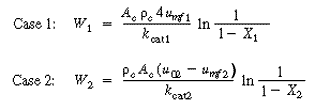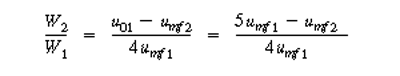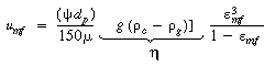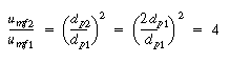Chapter 15: Diffusion and Reaction in Porous Catalysts
Professional Reference Shelf
Example CD12-6: Effect of Particle Size on Catalyst Weight--Slow Reaction
Suppose that you are operating at five times the minimum fluidization
velocity, uo = 5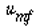 What would be the effect of doubling
the particle diameter on the catalyst weight for the same throughput and conversion? What would be the effect of doubling
the particle diameter on the catalyst weight for the same throughput and conversion?
|
|||
| Solution | |||
| Substitution for u0 into Equation (CD12-89) gives | |||
|
|
(CDE12-7.1) (CDE12-7.2) |
||
| Since the temperature remains constant and there are no inter- and intraparticle resistances, kcat1 = kcat2 , the throughput (u01 = u02 ) and conversion (X1 =X 2 ) are the same for cases 1 and 2. The ratio of Equations (CDE12-7.1) and (CDE12-7.2) yields | |||
|
|
(CDE12-7.3) | ||
| Recalling Equation (CD12-25) gives | |||
|
|
(CDE12-7.4) | ||
and neglecting the dependence of 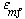 on dp, we see that the only parameters
that vary between case 1 (dp
) and case 2 (dp2= 2dp1 ) are on dp, we see that the only parameters
that vary between case 1 (dp
) and case 2 (dp2= 2dp1 ) are 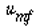 and W. Taking the ratio of and W. Taking the ratio of 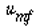 2to 2to
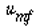 1 and substituting
for d p2 in terms of dp1
, we obtain 1 and substituting
for d p2 in terms of dp1
, we obtain
|
|||
|
|
(CDE12-7.5) | ||
| and therefore | |||
|
|
(CDE12-7.6) | ||
| Thus in the situation we have postulated, with a first-order reaction and reaction limiting the bed behavior, doubling the particle size will reduce the catalyst by approximately 75% and still maintain the same conversion. |