Proof of Mixing Vector Geometry

The mole balance around the junction gives:

F1*cA1 + F2*cA2 = F3*cA3
F1 + F2 = F3
=> cA3 = (1-a)cA1 + a*cA2; a=F2/F3

This is just the lever arm rule. Subtracting cA1 from both sides:

cA3 - cA1 = a(cA2 - cA1)

Also, for the other components

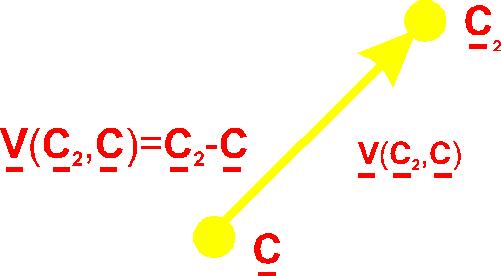
cB3 - cB1 = a(cB2 - cB1)
etc.

So in vector notation

c₃ - c₁ = a(c₂ - c₁) = a*v;

So the mixing vector points from c₁ to c₂

Mixing vector geometry