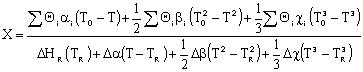
Energy Balance for Adiabtaic Reactors
Energy Balance for Adiabtaic Reactors

Let's calculate the volume necessary to achieve a conversion, X, in a PFR for a first-order, exothermic reaction carried out adiabatically. For an adiabatic, exothermic reaction the temperature profile might look something like this:

The combined mole balance, rate law, and stoichiometry yield:
, wav mp3

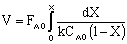
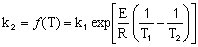
Need to relate X and T. Use the Energy Balance to

The user friendly forms of the energy balance we will focus on are outlined in the following table.

User friendly equations relating X and T

1. Adiabatic CSTR, PFR, Batch, PBR achieve this:                                    wav mp3

2. CSTR with heat exchanger, UA(Ta-T) and large coolant flow rate.

3. PFR/PBR with heat exchange

3A. In terms of conversion

3B. In terms of molar flow rates

4. For Multiple Reactions

In the material that follows, we will derive the above equations.

Energy Balance: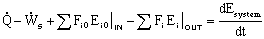
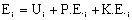
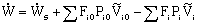
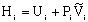
General Energy Balance: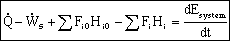
For steady state operation: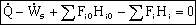
            wav mp3

We need to put the above equation into a form that we can easily use to relate X and T in order to size reactors. To achieve this goal, we write the molar flow rates in terms of conversion and the enthalpies as a function of temperature. We now will "dissect" both Fi and Hi.

Flow Rates, Fi
For the generalized reaction:

In general,

Enthalpies, Hi

Assuming no phase change:

Mean heat capacities:
wav mp3
    Heats of Reaction
Energy Balance with "dissected" enthalpies:
For constant or mean heat capacities:
            wav mp3


Adiabatic Energy Balance: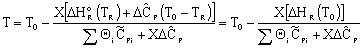
Adiabatic Energy Balance for variable heat capacities:


Go Back