|
Type of Reactor |
Characteristics |
|
Continuously Stirred Tank Reactor (CSTR) |
Arranged as one long reactor or many short reactors in a tube bank ; no radial variation in reaction rate (concentration); concentration changes with length down the reactor |
Kinds of Phases Present |
Usage |
Advantages |
Disadvantages |
1. Primarily Gas Phase |
1. Large Scale 2. Fast Reactions 3. Homogeneous Reactions 4. Heterogeneous Reactions 5. Continuous Production 6. High Temperature |
1. High Conversion per Unit Volume 2. Low operating (labor) cost) 3. Continuous Operation 4. Good heat transfer |
1. Undesired thermal gradients may exist 2. Poor temperature control 3. Shutdown and cleaning may be expensive |
General Mole Balance Equation
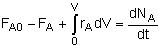
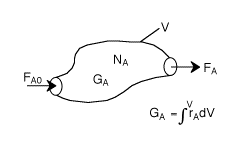
At steady state-
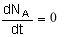
Differentiating, that gives-
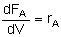
For single reactions in terms of conversion-
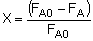
The differential form of the PFR mole balance is-
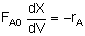
The integral form is-

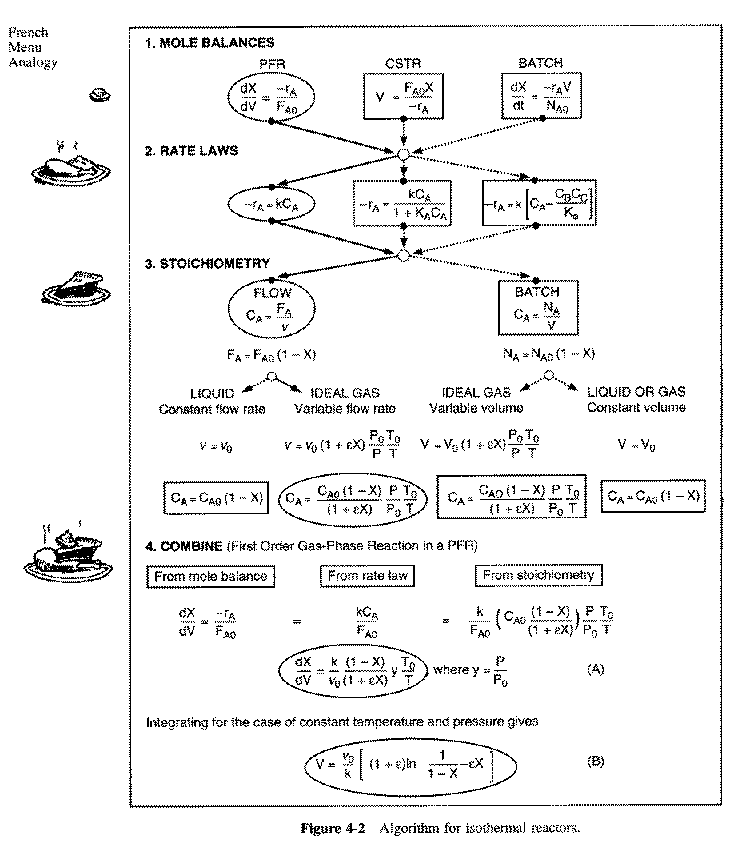
EXAMPLE
Gas Phase Elementary Reaction Additional Information only A fed P0 = 8.2 atm T0 = 500 K CA0 = 0.2 mol/dm3 k = 10 dm3/mol-s vo = 25 dm3/s
PFR Mole Balance: Rate Law: Stoichiometry: Gas: T = T0, P = P0 Combine: For X = 0.9: V = 45.3 dm3
Given -rA as a function of conversion, one can size any type of reactor. The volume of a PFR can be represented as the shaded area in the Levenspiel Plot shown below.
The integral to calculate the PFR volume can be evaluated using a method such as Simpson's One-Third Rule (pg 925):
Numerical Evaluation of Integrals
NOTE: The intervals () shown in the sketch are not drawn to scale. They should be equal.
EXAMPLE
Determine Xe for a PFR with no pressure drop, P = P0
Given that the system is gas phase and isothermal, determine the reactor volume when X = 0.8 Xe.
Reaction Additional Information CA0 = 0.2 mol/dm3
KC = 100 dm3/molk = 2 dm3/mol-min
FA0 = 5 mol/minFirst calculate Xe:
One could then use Polymath to determine the volume of the PFR. The corresponding Polymath program is shown below.

Using Polymath
Algorithm Steps Polymath Equations Mole Balance d(X)/d(V) = -rA/FA0 Rate Law rA = -k*((CA**2)-(CB/KC)) Stoichiometry CA = (CA0*(1-X))/(1+eps*X) CB = (CA0*X)/(2*(1+eps*X)) Parameter Evaluation eps = -0.5 CA0 = 0.2 k = 2 FA0 = 5 KC = 100 Initial and Final Values X0 = 0 V0 = 0 Vf = 500 Polymath Screen Shots
Equations
Plot of X vs. V
Results in Tabular Form
A volume of 94 dm3 (rounding up from slightly more than 93 dm3) appears to be our answer.