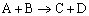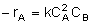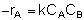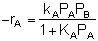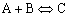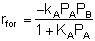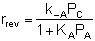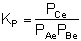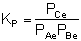The net rate of formation of any species is equal to its rate of formation in the forward reaction plus its rate of formation in the reverse reaction:
Example: Consider the exothermic, heterogeneous reaction

At low temperature, the rate law for the disappearance of A is
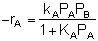 |
[Recall PA=CART] |
At high temperature, the exothermic reaction is significantly reversible:
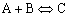
What is the corresponding rate law? Let's see.
If the rate of formation of A for the forward reaction (A + B 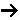 C) is
C) is
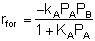
then we need to assume a form of the rate law for the reverse reaction that satisfies the equilibrium condition. If we assume the rate law for the reverse reaction (C  A + B) is
A + B) is
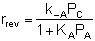
then:



and:
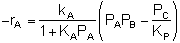


Does this rate law satisfy our requirement that, at equilibrium, it
must reduce to an equation that is thermodynamically consistent with
KP? Let's see.
From Appendix C we know
that for a reaction at equilibrium:
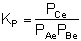
At equilibrium, rnet
 0, so:
0, so:

Solving for KP gives:
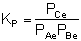


The conditions are satisfied.


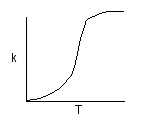
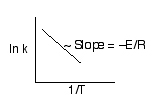
Activation Energy