We will always use this basic algorithm and then just add to these steps to it, e.g. the energy balance. We will not deviate from these first four steps.
The CSTR is always operating a the lowest concentration, the exit concentration. When say two CSTRs are in series, the first operates at a higher concentration, therefore the rate is greater, therefore the conversion is greater. The second reactor in series builds on the conversion in the first reactor. The conversion in the parallel scheme is the same as the conversion to the first reactor to the series scheme. See Figure p.50 and Example 4-2.
The PBRs in parallel are ued when there would otherwise be a large pressure drop in one long reactor or identically several PBRs connected in series.
You can have a pressure drop in liquid phase systems, but it does not affect the reaction rate because liquids are virtually incompressible and therefore the concentration does not change with pressure.
Not for a CSTR, only a PFR/PBR when there is a significant pressure drop.
- What is the Damköhler number?
See p.138 of text.
- How is the Damköhler (Da) number defined for a reaction
(A + B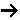 C) when the reaction is first order in A, first order in B, but
second order overall?
C) when the reaction is first order in A, first order in B, but
second order overall?
Just substitute the rate law evaluated entrance to the reactor, -rA0, [e.g. -rAo=kCAoCBo] into the definition
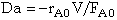 .
See p.138.
.
See p.138.
- Is Da always indicative of certain conversion?
Yes, for irreversible reactions.
- How does defining an extra variable, the Damk�hler number,
save us time and confusion, as opposed to solving without it? When
should it be used?
It serves as rule of thumb. When Da < 0.1 then X < 10% and when Da >10 then X >90%. See margin note p.138 of Ch.4.
Batch experiments are most always easier to take the necessary data to determine k.
When you are short on time and want to get quick engineering estimates.
Good point. It would change the volume; however, catalyst decay by fouling is usually more important. See Ch.10.
It depends, if there are no side reactions, a chemical clean is probably not necessary. Also the larger the reactor the greater the cleaning time.
When studying catalytic reactions the rate law is developed in terms of partial pressure,
e.g. ![]() .
.
To rewrite the rate law just use ideal gas law to relate to concentrations CA and CB
![]()
and then write concentration in terms of conversion.
Writing partial pressures in terms of conversion
![]()
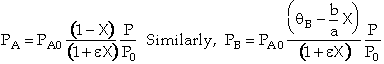
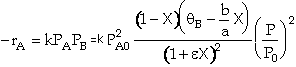
True but these are ideal CSTRs, and non ideal reactors and the perfect mixing assumption is discussed and modeled in Ch.13. Once we understand ideal reactors (perfectly mixed), we can easily model non-ideal reactors.
It does continue to react to some extent. It depends on the temperature in the pipe! However, these are ideal reactors. Different models for Non-ideal reactors are discussed in Chapters 13 and 14, but we must understand ideal reactors first.
Sometimes. See Lecture 6 on the CD-ROM.
The same is true for a PFR![]() If you increase
If you increase ![]() and you increase X.
and you increase X.
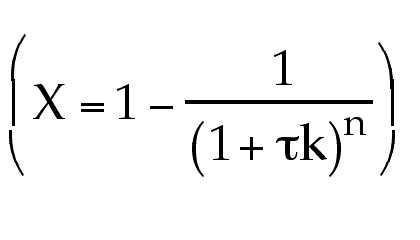 always the same no matter the order
of reaction?
always the same no matter the order
of reaction?
No! This equation is only for first order.
It is quite a good assumption for turbulent flow. It is not valid for Laminar flow - see Ch.13 p.831.
You can only use this relationship in the internal diffusion limited
regime shown in Figure 12-5, p.750. For a first order reaction ![]() with
with
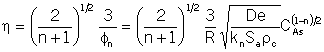 (12-35)
(12-35)
or lumping all the constants not involving particle size into a parameter, we have "a"
![]() Then
Then 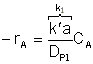 .
Thus
.
Thus ![]() then k2 = k1
then k2 = k1 ![]() for Pb. 4-23 one must use all of Figure 12-5. It can be shown that
Figure 12-5 can be represented as
for Pb. 4-23 one must use all of Figure 12-5. It can be shown that
Figure 12-5 can be represented as
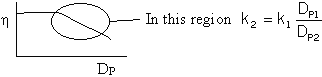
Yes, ![]()
NO!! The mole balance is 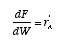
The relationship between reactor volume and catalyst weight is 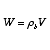
Substituting for W 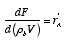
Then 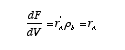
![]()
Neglecting ![]() X
X
![]()
For what values of ![]() X
is this valid?
X
is this valid?
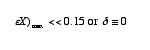
Yes, in the transition region one must use full equations for ![]()
It changes with packing of catalyst, but usually very little for the PBR and catalysts commonly used.
Because you can't relate the concentration of the product diffusing out, CB, and X.
The onstream time for flow systems is much much greater than the down time for cleaning and repair.
Yes, especially when O2 is one of the reactants.
In this region (i.e. after the knee) the reaction is in equilibrium and the rate of removal of B is what limits the overall rate of reaction.
Most liquids do not change density during the course of the reaction.
In Case I, it was for a batch system, thus no flow, and that is
why there is no vot term. If it was a semi-batch system plus immediate
evaporation: ![]()
You are only interested in the ratio Z/Zo being the same, we don't care if Z doesn't equal one.
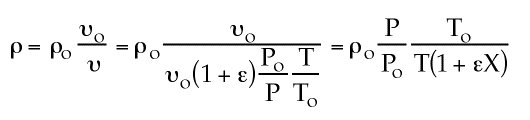 If epsilon is greather than 1, density is greater than if epsilon=0 because
If epsilon is greather than 1, density is greater than if epsilon=0 because
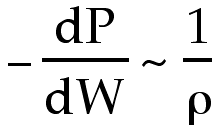
A larger density results in a smaller change in pressure.