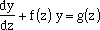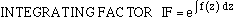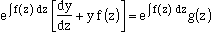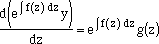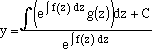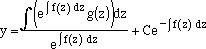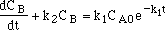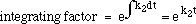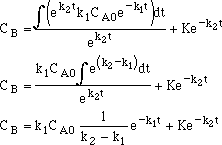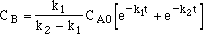| Problem - You want to integrate
|
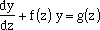
| (1)
|
| However, that f(z)y term really messes things up! If you only had an expression of the form
|
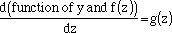
| (2)
|
things would be much easier, then you could integrate with respect to z and find y(z). How can you combine f(z) and y to get this simplification? First note that 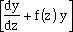 is of the form of the derivative of a product, so examine first the product y u, where u is some function of f(z) you still have to define. Recall is of the form of the derivative of a product, so examine first the product y u, where u is some function of f(z) you still have to define. Recall
|
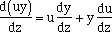
| (3)
|
| That's looking close to the left hand side of equation (1), but there is a "u" in front of the dy/dz term, and a du/dz expression where f(z) is. If you had a form of u such that du/dz = u f(z), then you could manipulate equation (3):
|
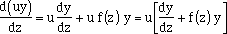
| (4)
|
| where the term in brackets is the left hand side of equation (1). You need du/dz = u f(z). Recall
|
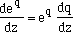
| (5)
|
If you define 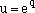 and f(z) = dq/dz (i.e. and f(z) = dq/dz (i.e. 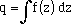 , then , then
|
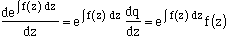
| (6)
|
This satisfies the condition that du/dz=u f(z). That's the ezpression you needed! Therefore,  , and substituting into equation (4), , and substituting into equation (4),
|

| (7)
|
| where the term in brackets is the left hand side of equation (1).
CONCLUSION: If your problem is of the form
|
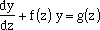
| (1)
|
| you can multiply both sides of the equation by the
|
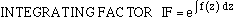
|
|
| (which you should be able to evaluate, since you know f(z)), to yield
|
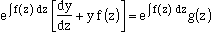
| (9)
|
| or, substituting from equation (7)
|
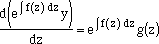
| (10)
|
| so that
|
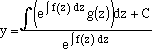
| (11)
|
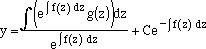
| (12)
|
| EXAMPLE
|
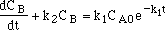
|
| f(t)=k2, so
|
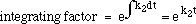
|
| From equation (12), the solution is then
|
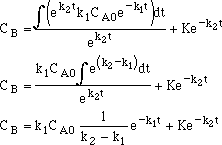
|
| The constant can be obtained from the intitial condition that at t=0, CB=0;
|
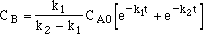
|
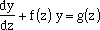
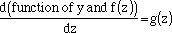
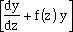 is of the form of the derivative of a product, so examine first the product y u, where u is some function of f(z) you still have to define. Recall
is of the form of the derivative of a product, so examine first the product y u, where u is some function of f(z) you still have to define. Recall
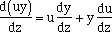
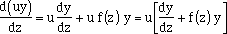
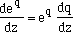
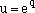 and f(z) = dq/dz (i.e.
and f(z) = dq/dz (i.e. 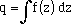 , then
, then
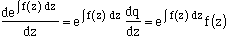
 , and substituting into equation (4),
, and substituting into equation (4),