9. Unsteady State Non-Isothermal Reactor Design*

Topics

  1. Batch Reactors with Heat Effects Example
  2. Control of Chemical Reactors
  3. Linearized Stability Theory
  4. Predicting the Behavior of a CSTR using LST

Batch Systems with Heat Effects Example top

Balance on a system volume that is well-mixed:

Adiabatic batch reactor with no work:



Polymath

The following reaction occurs in a batch reactor:

1)

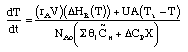2)

3)

4)

5)

6)

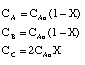7)

Parameter Values

Adiabatic Reaction

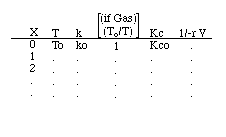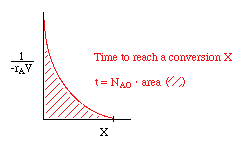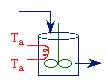
or use one of the integration formulas, e.g.: , to find the reaction time, t. Even better, use Polymath.

Cooling:

 
Batch Reactor with External Heating
Text Example 9-2
Questions related to Problem 9-2


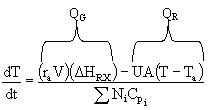
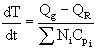
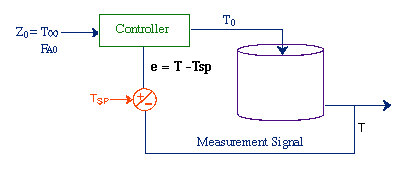
Control of Chemical Reactors top

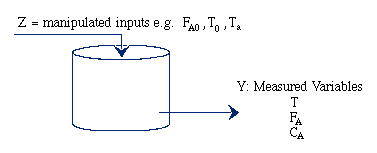Unsteady State CSTR:

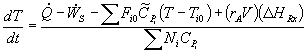For a batch reactor, FAO = 0

Integral Control

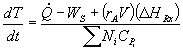For the reaction     in a CSTR:

Proportional Control


Integral Controller


Proportional-Integral Control

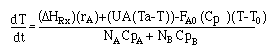Linearized Stability Theory top
Energy Balance (Applied to a CSTR)

1.

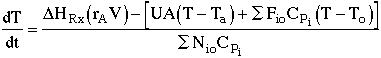2.

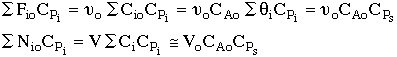3.

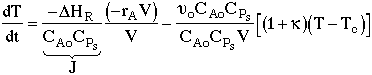4.

 
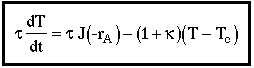CSTR Mole Balance

5.

6.

 
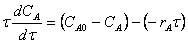Manipulating the Energy and Mole Balances

Let andsignify steady state values. Then at steady state:

7.

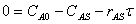Adding equations (6) and (7):

8.

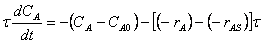Linearizingby expanding it in a Taylor Series:

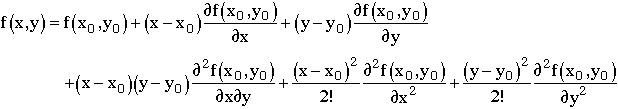To obtain:

9.

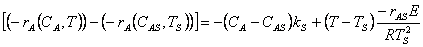10.

Let   

      
      

11.

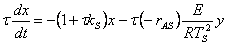12.

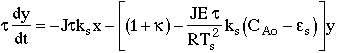13.

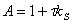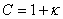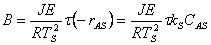Using these substitutions, we can arrive at the following equations that describe the behavior of temperature and concentration, when the steady state conditions are perturbed in a CSTR:

14.

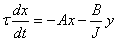15.

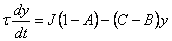16.

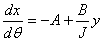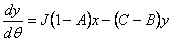17.

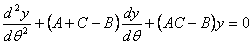18.

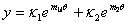19.

20.

21.

22.



Predicting the Behavior of a CSTR using LST top

At time t = 0, y1 = y10, where:

Making use of Equation 20

we notice that for the case of b2 = 4c:

if b < 0 ,   then the amplitude (i.e., T - TS) will increase

if b > 0 ,   then the amplitude (i.e., T - TS) will decrease

and that:

if b2 > 4c ,   thenis real (i.e., non-oscillatory behavior)

if b2 < 4c ,   thenis imaginary (i.e., oscillatory behavior)


 

  1. Critically damped: b is positive andis real
  2. Unstable growth: b is negative andis real
  3. Oscillatory and damped: b is positive andis imaginary
  4. Oscillatory: b is zero andis imaginary
  5. Unstable growth oscillation: b is negative andis imaginary

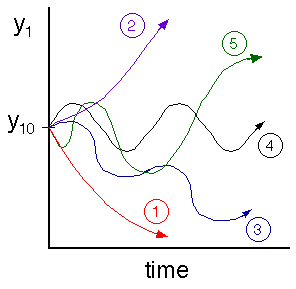Reference:
R. Aris, Elementary Chemical Reactor Analysis, Prentice Hall, New Jersey, (1969).


Object Assessment of Chapter 9
 

* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .

top