| Active Intermediates / Free Radicals (PSSH) | top |
An active intermediate is a molecule that is in a highly energetic and reactive state It is short lived as it disappears virtually as fast as it is formed. They are short lived CA 10-14s and present in very low concentrations. That is, the net rate of reaction of an active intermediate, A*, is zero.
The assumption that the net rate of reaction is zero is called the Pseudo Steady State Hypothesis (PSSH)
The active intermediates reside in the trough of the reaction coordinate as shown below for ![]() in the reaction studied by Zewoil.
in the reaction studied by Zewoil.
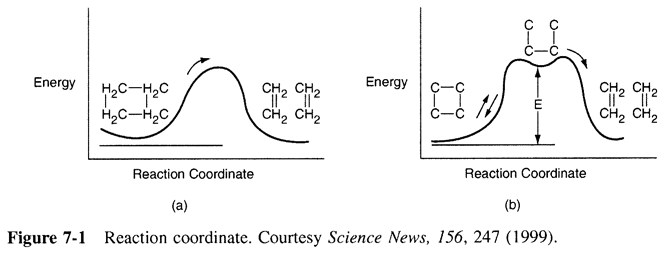
The reaction

has an elementary rate law

However... Look what happens to the rate as the temperature is increased.

Why does the rate law decrease with increasing temperature?
![]()
Mechanism:
 |
(1) |
 |
(2) |
 |
(3) |

The PSSH assumes that the net rate of species A* (in this case, NO3*) is zero.

Solving for NO3*





This result shows why the rate decreases as temperature increases.
| Enzymes | top |
Enzymes are protein like substances with catalytic properties.
|
Enzyme unease. [From Biochemistry, 3/E by Stryer, copywrited 1988 by Lubert Stryer. Used with permission of W.H. Freeman and Company.] |
It provides a pathway for the substrate to proceed at a faster rate. The substrate, S, reacts to form a product P.




A given enzyme can only catalyze only one reaction. Urea is decomposed by the enzyme urease, as shown below.
It has been proposed that an artificial kidney to remove urea from the blood could contain encapsulated enzymes and be worn externally.




The corresponding mechanism is:
 |
| Michaelis-Menten Equation
Inverting yields: |
 |
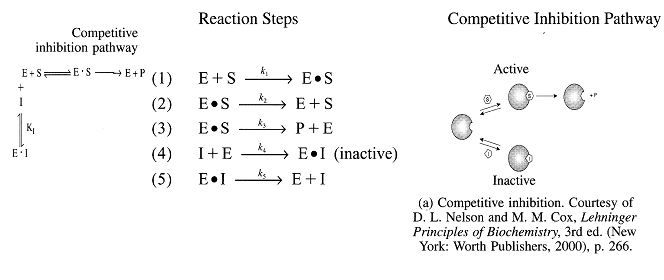

Uncompetitive Substrate Inhibition
E + S  E •
S (Inactive)
E •
S (Inactive)
S + E•S  S•E•S (Inactive)
S•E•S (Inactive)
E•S  P + E
P + E
The Uncompetitive Substrate Inhibition rate law is


The following movie was made by the students of Professor Alan Lane's chemical reaction engineering class at the University of Alabama Tuscaloosa
| Bioreactors | top |

|
||||||
Rate Laws |
 |
|||||
| |
||||||
Stoichiometry |
||||||
A.) Yield Coefficients |
 |
|||||
 |
||||||
B.) Maintenance |
 |
|||||
 |
||||||
A Word of Caution on |
||||||
A.) Growth Phase |
 |
|||||
B.) Stationary Phase |
 |
|||||
Mass Balances |
||||||
Cell: |
 |
|||||
Also, |
||||||
Substrate: |
 |
|||||
 |
||||||
| 1.) | d(Cc)/d(t) = - D*Cc + (rg - rd) |
| 2.) | d(Cs)/d(t) = D*(Cso - Cs) - Ysc*rg - m*Cc |
| 3.) | d(Cp)/d(t) = - D*Cp + Ypc*rg |
| 4.) | rg = (((1 - (Cp/Cpstar))**0.52) * mumax*(Cs/(Ks + Cs))*Cc |
| 5.) | D = 0.2 |
| 6.) | kd = 0.01 |
| 7.) | rd = kd*CC |
| 8.) | Cso = 250 |
| 9.) | Ypc = 5.6 |
| 10.) | m = 0.3 |
| 11.) | mumax = 0.33 |
| 12.) | Ysc = 12.5 |
| 13.) | Ks = 1.7 |
| Polymath Screen Shots |
|
|

1.) Neglect Death Rate and Cell Maintenance |
|||
2.) Steady State |
 |
||
 |
|||
 |
|||
 |
|||
 |
|||
| |
|||
| Washout |  |
||
| Maximum Production Rate Production Rate = |
|||
| Dividing by the reactor volume, V, which is constant | |||
 |
|||
Substituting for CC
|
|||
|
|||
| Pharmacokinetics | top |






 The complete description of the model and the model paramenters can be found in this journal article.
David M. Umulis, Nihat M. Gurmen, Prashant Singh, H. Scott Fogler. "A physiologically based model for ethanol and acetaldehyde metabolism in human beings," Alcohol 35 (2005).
The complete description of the model and the model paramenters can be found in this journal article.
David M. Umulis, Nihat M. Gurmen, Prashant Singh, H. Scott Fogler. "A physiologically based model for ethanol and acetaldehyde metabolism in human beings," Alcohol 35 (2005).





See Professional Reference Shelf 7.5
| Polymerization | top |
Polymers are macromolecules built up by the linking together of large numbers of much smaller molecules. The smaller molecules are called monomers and they repeat many times.
A polymer is a molecule made up of repeating structural (monomer) units.

Examples of Polymers
Poly (vinyl chloride)
Natural Polymers
Proteins
DNA/RNA
Cellulose
Fats
StarchSynthetic Polymers
Name
Structural Repeating Unit (mer)
Uses
Poly (vinyl chloride)
Pipes
Polyethylene
High density:
Plastic cupsLow density:
Sandwich bags
Polystyrene
Coffee Cups
Poly (acrylic acid)
Superglue (Dow)
Poly (cyano acrylate)
Superglue
Poly (vinyl acetate)
Chewing gum
Poly (vinyl alcohol)
Shampoo/Thickener
Poly (ethylene glycol)
Stealth molecule
Poly (methyl methacrylite)
Plexiglas
Poly (2-hydroxyethyl methacrylate)
Contact Lenses
Poly (tetra fluoro ethylene)
Teflon
Poly (ethylene teraphthalate)
Coke bottles
Spinable fibers
A. Names/Nomenclature
Polymers that are synthesized from a single monomer are named by adding the prefix poly such as polyethylene. However, a parenthesis is placed after the prefix poly when the monomer has a substituted parent name or multiword name such as poly (acrylic acid) or poly (vinyl alcohol).
Homopolymers consist of a single repeating unit. All of the above are examples of homopolymers.
B. Polymer structure
1. Linear
Linear HDPE (70-90% crystalline)
2. Stereoregularity
Can Crystallize.
a.
Botactic = isotatic = same side
b.
Syndiotatic = alternating
c.
Atactic = random
Head to head (1,2 addition)
Head to tail (1,3 addition)
3. Branched Type A: Long Branches Off Backbone

Branched Type B: Short Branches Off the Backbone
Branched Type C: Branches on Branches Off the Backbone
4. Cross linked
C. Copolymers
More than one repeating unit.

For example, copolymers used to make records.
PVC - hard - irrigation pipes, hard to engrave
PVAc - easy to engrave
PVC + PVAc copolymerphonograph records (these are a thing of the past)
FIVE TYPES OF COPOLYMERS
Alternating
QSQSQS
Poly (vinyl acetate-alt-vinylchloride)
Block
QQQSSS
Poly (vinyl acetate-b-vinyl chloride)
Graph
QQQQQ
. . . . . |
. . . . . SSSSPoly (vinyl acetate-g-vinyl chloride
Random
QSSQQQSQSSS
Poly (VAc-co-VC)
Statistical
QSSQSQQSS
D. What affects polymer properties
• Chemistry
• Molecular Weight (
) and Molecular Weight Distribution

Weight Average Molecular Weight

Molecular Weight Distribution
• Crystalinity
Amorphous Phase (Non-crystalline Phase) no order or orientation
|
|
Tg - characteristic of amorphous state Rubbery Below glass transition temperature, Tg, there is a cessation of virtually all molecular motion (vibration , rotation). |
Crystalline Phase gives an order to the structure.
|
|
Order means crystallinity Crystalline Above the crystalline melting temperature, Tm, thre is no order. Fraction of total polymer that is in the crystalline state is the degree of crystallinity |
• Cross linking
• Branching
• Tacticity
• Head to head attachment vs. head to tail attachment
E. Molecular Weight (MW)
1. Measurement
Membrane osmometry

Gel permeation chromatography

Viscosity

Light scattering
2. Calculation
Number average molecular weight

Weight average molecular weight


Hence ![]() gives a truer picture of the average molecular weight.
gives a truer picture of the average molecular weight.

3. Polydispersity
TWO TYPES OF HOMOGENEOUS POLYMERIZATION: STEP AND CHAIN
Step Polymerization. Monomer must be bifunctional. Polymerization proceeds by the reaction of two different functional groups. Monomer disappears rapidly, but molecular weight builds up slowly.

All species are treated as polymers. Mostly used to produce polyesters and polyamides.
Chain Polymerization. Requires an initiator. Molecular weight builds up rapidly. Growing chains require 0.0001 to 1 to 10 seconds to terminate. Have high molecular weight polymers right at the start.

I. Step Polymerization
A. Functional Groups
1. Different functional groups on each end of monomer.
Structural Unit
Here the structural unit is the repeating unit.
2. Same functional groups on each end. Example: diamines and diols
Two structural units
and

Repeating unit =
B. Polymerization Mechanism
Monomer dimer ----> trimer ----> tetrameter ----> Pentamer ---->
C. Structural Units
The number of structural units equals the number of bifunctional monomers present.
1. Monomers with different functional groups - one structural unit.
Here the repeating unit is the structural unit.
Let p = fraction of functional groups of either A or B that have reacted.
Let M = concentration of either A or B functional groups at time t.
Let M0 be the concentration of either A or B functional groups initially
Let N = total number (concentration) of polymer molecules present at time t.
Let N0 = total number of polymer molecules initially
Let MA = number of functional groups of A at time t.
Let MA0 = number of functional groups of A initially.
= number average degree of polymerization. It is the average number of structural units per chain.
therefore
the number average molecular weight.
Where
is the mean molecular weight of the structural units and
is the molecular weight of the end group.
D. Monomers with Same End Group
For a stoichiometric feed the number of A and B functional groups the same.
E. Stoichiometry Imbalance in the Feed
1. Stoichiometry Imbalance Type 1: Monomers with thesame end group and r not equal to 1
The maximum number average chain length is greatly reduced if the initial feed is not exactly stoichiometric
If p = 1 then
2. Stoichiometry Imbalance Type 2: Monomers with different end groups. Monofunctional Monomer Present
, [A-R-A]o =[B-R-B]o =MAo
[B-C]o =MBo
3. Stoichiometry Imbalance Type 3: Monomers with different end groups. Monofunctional Monomer Present
REACTION BETWEEN A DIOL (HOROH) AND A DIBASIC ACID (HOOCR1COOH)

Let
Then
Overall Reaction:
The Mechanism
Rate Law:
(1)
(2)
(3)
Let
-- =
~ =
The rate limiting step is Reaction (2)
Assume Reaction (1) is essentially in equilibrium

,
Case 1: The acid itself acts as a strong acid catalyst:
[HA] º [COOH] and Stoichiometric Feed.
As the reaction proceeds and more ester is produced, the solution becomes less polar. As a result the uncatalyzed carboxylic acid becomes the major catalyst for the reaction, and the overall reaction order at high conversion is well described by a third order reaction (Case 1). The high conversion region is of primary importance because this region is where the high molecular weight polymers are formed.
At low conversions the solution is more polar and the proton, H+ is the more effective catalyst (Case 2) than the unionized carboxylic acid. Under these conditions, the reaction is self catalyzed and the reaction is 5/2 order.
Case 2: Self catalyzed but acid acts as a weak acid catalyst, not completely dissociated
[HA] = [-COOH]

Case 3: External Acid Catalyzed H+ is constant
F. Kinetics of Step Polymerization
(1)
k is defined wrt the reactants
Why 2k? Because there are two ways A and B can react (thus, 2k)
![]()
(2)
(3)
For all reactions of P1
In general for j ? 2
For j = 2
Mole balance on polymer of length j, in terms of the concentration Pj in a batch system


If we proceed further it can be shown that

Total number of polymer molecules (i.e. functional groups of either A or B) =
Mole fraction
This is the Flory Distribution for the mole fraction of molecules with chain length j.
The weight fraction is just
W = total weight =
G. Flory Distribution-Probability Approach
Rule: The probability of several events occurring successively in a particular way equals the product of the probabilities that each event happens that way.
P = probability that an A group will has reacted
(1-P) = probability group has not reacted.
A - R - B
HO - R C OO - H

|
|
|
|

![]()

Mo = number of functional groups initially (no. of molecules)
M = number of functional groups remaining
Number distribution function.
Weight distribution function


On a number average basis there will always be more monomer than polymer.
II. Chain Polymerization
A. Free Radical
Example: Polyethylene
Linear addition


Back biting









Branched Polyethylene
resulting low density (0.92)
B. Cationic Polymerization
C. Anionic Polymerization
D. Ziegler-Natta Polymerization
Ziegler-Natta Catalyst
Steps in Polymer Chain Growth
(4) Desorption from active site

+
to produce linear polymer: Eq. High Density Polyethylene (0.98) (HDPE)
Chain polymerizations require an initiator.
INITIATION
This reaction produces the formation of the Primary Radical
PROPAGATION
TERMINATION
Transfer
Addition
To solvent
To monomer
To chain transfer agent
To initiator
Disproportionation
MORE ABOUT INITIATION
Types of initiators, homiletic, photo
Typical Initiators for Homolytic Dissociation
Temperature Range
Initiator
(1)
50-70
Azobisisobutyranitride (ABIN)
(2)
70-90
Acetyl Peroxide
(3)
80-95
Benzyl Peroxide
Kinetics

Initiator Efficiency "f"f = fraction of radicals produced in the homolysis reaction that initiate polymer chains. It is a measure of waste of initiator.
How to determine f experimentally
- In AIBN measure N2 evolution compare number of radicals produced with number of polymer molecules obtained.
- Tag initiator 14C or 35S
- Use scavengers - to stop growth.
 Lab-on-a-Chip
Lab-on-a-Chip
INITIATION
PSSH applied to initiator
(1) (2) PROPAGATION
For all radicals the total rate of propagation
= total concentration of radicals (R1 + R2 + R3 . . . Rn)
Monomer balance
Long Chain Approximation (LCA)
The rate of disappearance of monomer, -rm,
TERMINATION
1. Chain transfer
A.
To monomer
Total rate of transfer for all radicals
B.
To solvent
C.
Transfer to a chain transfer agent
D.
Transfer to initiator
2. Dispropriation Termination
Disproportionation
Define kd wrt reactants
i.e.
Net rate of termination of all radicals by dispropriation. For every dead polymer molecule that is formed, one live polymer radical is lost.
3. Addition Termination
where ka is defined wrt to the reactant.
The net rate of termination of j radicals will all the Rk radical (k = 1, 2, ?)
The net rate of termination of all radicals is
PSSH Applied to All Free Radicals
Recall
Example Termination by the Initiator Primary Radicals, I
Independent of Initiator Concentration


Dead ended polymerization occurs when the initiator concentration decreases to such a low value, the half life of the polymer chains approximates half life of initiator
Polymerization of Isoprene initiated by azobisisolulyronitride.
Kinetic Chain Length
The kinetic chain length v is the average number of monomer molecules consumed (polymerized) per radial that initiates a polymer chain.
Chain Transfer
In Principles of Polymerization 3/e by George Odian, the definition of Rt, the factor of 2 is incorrect but does not matter because it cancels out since Rt is dived by 2 in the denominator in later equations. Also note Eqn. (3-118a) in Odians is altogether incorrect.
Let the transfer coefficient be defined by
(1) (2) (3) (4)
Term (1)
Canceling terms
Term (4)
Solving for I2
The Mayo-Walling Equation
Let?s neglect the term
For styrene
In benzyl peroxide
CM = 0.00006
CI = 0.055
In benzene
CS = 2.3 ´ 10?6
In Butyl mercaptan
CS = 21.1
Increasing the initiator concentration decreases
Increasing the monomer concentration increases
Further determination of Rate Constant
1. Dilatometry
Volume charge
2. Spectroscopically measure I2(t) and M(t)

B. Batch - Method of Initial Rates
Many experiments
Steady State Measurement
CSTR
No Chain Transfer

Determining Chain transfer Constants
A. Only transfer to chain transfer agent S
Hold M and I constant, vary S
B. Transfer to monomer, initiation and a chain transfer agent
Hold I and S constant, vary M
Change I and repeat, the intercept will be the same but slope will be different, S2. Change S and repeat S3. Three equations and 3 unknowns. Could also use regression.
Transfer Constants
A. To Monomer
0.00005 < CM < .0015
CM is generally small, however chain transfer to monomer for vinyl chloride is sufficiently high to limit the molecular weight so that the maximum molecular weight of PVC is 50,000 to 500,000.
B. To Initiator
CI is a function of both the initiator and the reaction
0.0008 < CI < 0.3
Peroxides are usually the strongest chain transfer agents.
C. To Chain Transfer Agent
For styrene
0.000002 < CS < 21
(Benzene) < CS < (n Butyl mercaptan)
Chain Transfer to Polymer, CP
Chain transfer to polymer produces branched polymers.
It is not important in determining CI, CM and CS because they are determined at low conversion.
CP involves the determination of the number of branches produced relative to the number of polymer molecules polymerized.
CP is the order of 10?4
The branching density, r , is the number of branches per monomer molecule polymerized.
For CP = 10?4 and 80% conversion, there will be 1.0 branches per 104 monomer units polymerized. There is one branch for every 4,000 to 10,000 monomer units and for a polymer molecular weight of 105 ? 106 this corresponds to 1 polymer chain in 10 containing a branch.
Polyethylene
1. Short branches (less than 7 carbon atoms)
Formed by backbiting. Short branches out number the long branches by a fact of 20-50. They affect crystallinity giving maximum crystallinity of 60-70%.
2. Long branches ? formed by normal chain transfer to polymer.
Energetics (Free Radical)
Therefore chain transfer becomes more significant as temperature increases!!!
Chain Polymerization
Ionic Polymerization
Cationic
Used for monomers with electron releasing substituents
(a) (b) (c) (d)
e.g. alkoxy, 1,1?dealky
(a) covalent species, (b) tight ion pair, (c) loose ion pair, (d) free and highly solvated ion
Anionic
Used with monomers possessing electron withdrawing groups, e.g. nitride, carboxyl.
Anionic
High molecular weight. No chain-chain termination.
Initiation
Alkyllithium used because soluble in hydrocarbon solvents.
Potassium amide
Propagation
No effective termination - complete consumption of monomer to form living polymers.
Termination by:
a. Impurities
Moisture
b. Deliberate addition of chain transfer agent
c. Spontaneous
Hydride elimination, i.e.
Comparison with free radical polymerization
Free Radical:
Concentration of radicals is 10?9 to 10?7 mol/dm3
Anionic:
Concentration of propagation anions is 10?4 to 10?2 mol/dm3
In hydrocarbon solvents
is 10-100 times smaller than kP
In either solvents
is 10-100 times larger than kP
Benzene
Tetrahydrofuran
1,2-Dimethoxyethane

2
550
3,800
Other values are given in Odian p.412
Why do the rates of polymerization vary by several orders of magnitude in different solvents?
Kinetics of Ion/Ion Pair Initiation/Polymerization
Initiation
Summing over all radicals
where
is the concentration of
and all radicals initiated with
and
is the concentration of
and radicals initiated with
We assume the ion and the ion pair are in equilibrium with the "salt."
Let
be the total concentration of all types of anionic living propagating centers.
where Io is the total amount of initiator added.
For small degrees of dissociation
If K ~ 10?8
and
then
If K ~ 10?6 then
Polymerization of Styrene




160
80
22

2.2
1.5
0.02

6.5
6.5
6.5
Data of Bhattacharya et al., J. Phys Chem. 69, p.612 (1965)
So we see that different solvents bring about different degrees of dissociation of the initiator resulting in different specific reaction rates.
Anionic Polymerization
1. Determining the living polymer concentration as a function of time
For complete dissociation of the iniator
Assumptions
Initiation is instantaneous, R10 = Io
2. No termination
Case 1 ko >> kp Immediate rate formulation of primary radical

Propagation with No termination
For the live polymer with the largest chain length n
Summing all these equations
Constant live polymer concentration
Let dq = kP M dt
t = 0, q = 0, R1 = Io
Convert back to real time from scaled time
Very small t (i.e., small IokPt)
Very large t (i.e., large IokPt)
Distribution of molecular weights of living polymers
Next consider a different set of initiation conditions
Case 2 ko = kp
Anionic Polymerization in a CSTR

Monomer Balance
Balance on R1
Balance on Rj
Psuedosteady State Hypothesis (PSSH)
Case 1 ko is essentially (i.e., ko >> kp) infinite. Io is reacted immediately upon mixing with monomer to form R10
There is no initator, I, in the reactor
where
Substituting for
Case 2 ko is finite
j = 1
* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .