| Diffusion and Reaction in Catalyst Pellets | top |
We now focus on steps 2 and 6 of our catalytic reaction . We shall carry a mole balance
on species A as it diffuses and reacts in a catalyst pellet.

1. Mole Balance (on material between r and r + delta r) |
|||
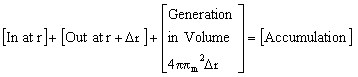   |
|||
2. Rate Law / Constitutive Equation |
|||
2A. Constitutive Equation |
|||
2B. Rate Law |
|||
|
|||
|
|||
3. Boundary Conditions |
|||
r = R, CA = CAs and r = 0, CA is finite |
|||
4. Combine and Put the Equation in Dimensionless Form |
|||
| Let |
|||
Boundary Conditions:
|
Then |
||
where |
|||
5. Concentration Profile (see text for derivation) |
|||
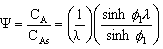 |
|||
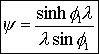 |
|||
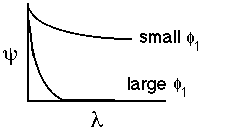
|
|||
for large values of phi1 the molecules don't diffuse very far into the pellet before they react |
|||
6. Effectiveness Factor |
|

For a first order reaction
trade off
But R is small and there are Large Pressure Drops through the bed.
But only part of the catalyst pellet is used so and
|
|
For the nth order reaction
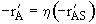 (12-38)
(12-38)
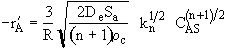 (12-39)
(12-39)
The true reaction order is
The true activation energy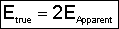 (12-43)
(12-43)
First read over Problem 12-7 on pages 798 and 799concerning the swimming of small animals. We shall divide the animal into a head section, a mid-piece, and a tail. ATP is produced in the mid-piece and is used as an energy source in the tail to swim. Therefore, ATP must get into the tail in order for the animal to swim.
![]()
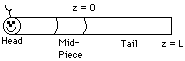
The rate of swimming is a function of the rate of diffusion into the tail. Therefore,
consider only diffusion in the tail.
1. Mole Balance
![]()
2. Constitutive Equation and Rate Law
![]()
![]()
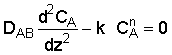
3. Boundary Conditions
at z = 0, CA = CA0
at z = L, dCA / dz = 0
4. Combine and Put the Equation in Dimensionless Form
![]()
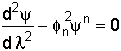
When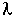 = 0, then
= 0, then![]() = 1.
= 1.
When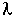 = 1, then
= 1, then![]() = 0.
= 0.
5. Solve for Concentration Profile
We shall assume the reaction is zero order:
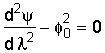

where:
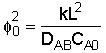
Solving:
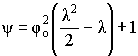
NOTE: effectiveness factor = 1.0 (for zero order reactions)
Finding the length of the tail of the creatures is easily found by equating the overall
rate (RA = 23 * 10-18 mol/s) to the rate of diffusion of ATP into
the tail using the above dimensionless concentration profile.
Dependence of Reaction Rate on Catalyst Particle Size:
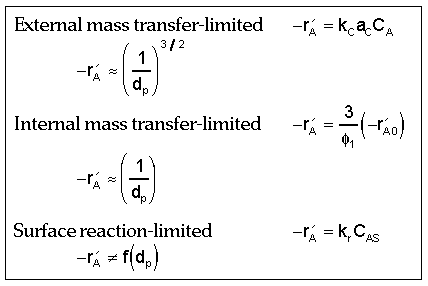
| Fluidization Engineering | top |
Ergun Equation for pressure drop across the bed,
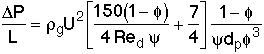
![]()
![]()
Nomenclature Note: In the text and lecture ![]() = porosity, while in the
CD-ROM section on Fluidization
= porosity, while in the
CD-ROM section on Fluidization ![]() = porosity. (Our apologies for the
inconsistency.)
= porosity. (Our apologies for the
inconsistency.)
At fluidization, the weight of the catalyst suspended equals the pressure drop (force) necessary to suspend it.
![]()
![]()
![]()
1. Minimum Fluidization Velocity, Umf
Solving equations [1] and [2]
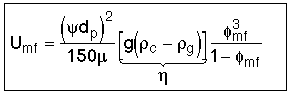
valid for Red < 10
Need
!!!
2. Minor Break Through to Find ![]()
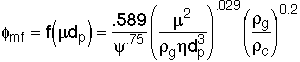
3. Terminal Velocity, ![]() (Make sure we don't blow the particles out of
the bed.)
(Make sure we don't blow the particles out of
the bed.)
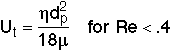
4. Slugging Velocity, ![]()
![]()
Umf < Uo< Ums< Ut
First calculate
![]()
then
![]()
then
![]()
![]()
For two or more bubbles, bubble rise is:
![]()
6. Factors That Determine Bubble Diameter (db)
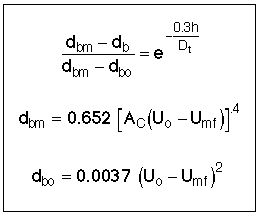
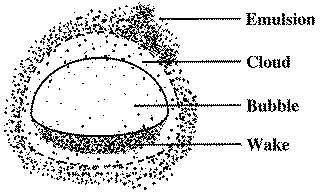
One usually evaluates db at h/2, but this is an area for future research.
![]() = Fraction of the total bed occupied by bubbles
(not including wakes)
= Fraction of the total bed occupied by bubbles
(not including wakes)
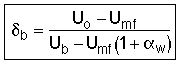
![]()
7. Balance on Solid
Solids flowing down = Solids flowing up in wakes
![]()
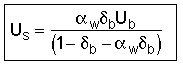
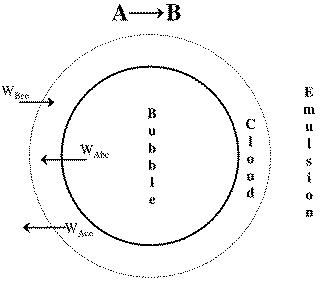
1. Transport Between Bubble and Cloud
![]()
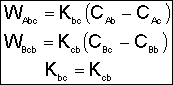
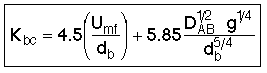
![]()
2. Transport Between Cloud and Emulsion
![]()
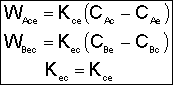
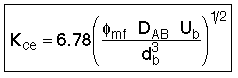
![]()
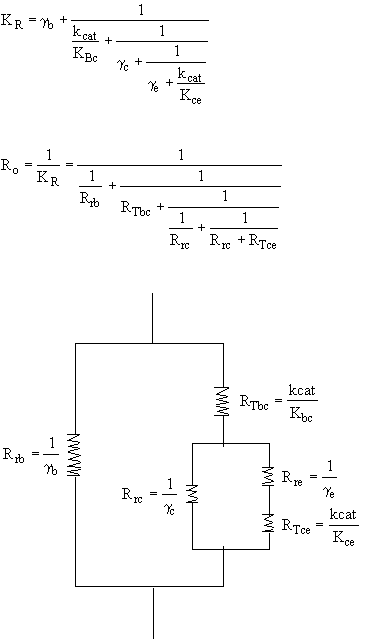
1. Balance on Bubble for Species A
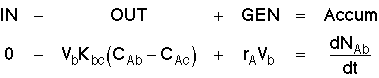
Divide by Vb, then:
2. Balance on Cloud for Species A
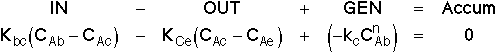
or

3. Balance on Emulsion for Species A
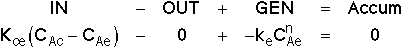
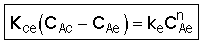
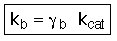
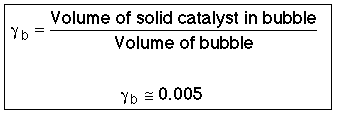
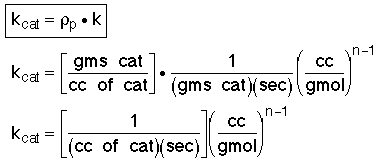

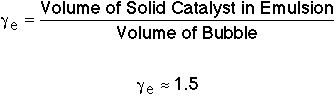
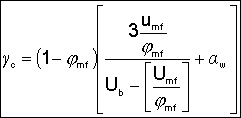
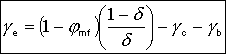
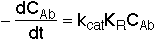
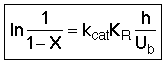
where:
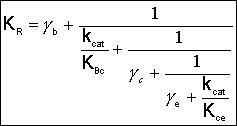
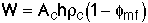

* All chapter references are for the 4th Edition of the text Elements of Chemical Reaction Engineering .
** This material was developed from notes by Dr. Lee F. Brown and H. Scott Fogler.