The second order reaction
![]()
occurs in the liquid phase. The RTD function for the reactor in which it is to be carried out is given by
E(t) for 0 < t < 10
E(t) = 0.01 (t–10) for 10 < t < 20
E(t) = 0.01 (30–t) for 20 < t < 30
E(t) = 0 for t > 30
![]()

This RTD function is the same one we previously studied in these lectures. The entering concentration is 2 molar and the specific reaction rate is 0.06 dm3/mol•s.
(a) What is the conversion after 30 seconds in a batch reactor?
(b) What conversion would be achieved in a PFR with the same mean residence time?
(c) What conversion would be achieved in a CSTR with the same mean residence time?
(d) What is the conversion predicted by the segregation model?
(a) What is the conversion after 30 seconds in a batch reactor?
Batch reactor![]()
![]()
![]()
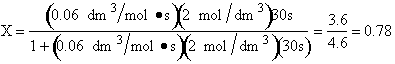
![]()
(b)
What conversion would be achieved in a PFR with the same mean residence
time?
PFR:![]()
![]()
![]()
![]()
![]()
(c) What conversion would be achieved in a CSTR with the same mean residence time?
CSTR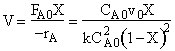
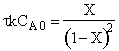
![]()
![]()
![]()
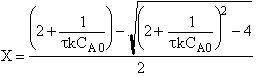
![]()
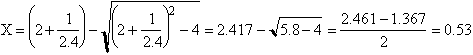
![]()
(d) What is the conversion predicted by the segregation model?
Segregation model

|
T |
0 |
10 |
15 |
17.5 |
20 |
22.5 |
25 |
30 |
|
E(t) |
0 |
0 |
.05 |
.075 |
.1 |
.075 |
.05 |
0 |
|
X(t) |
0 |
.55 |
.643 |
.67 |
.706 |
.73 |
.75 |
.78 |
|
XE(t) |
0 |
0 |
.032 |
.051 |
.071 |
.055 |
.038 |
0 |
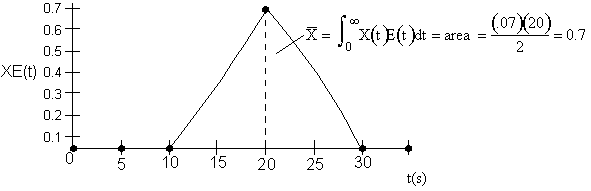
Plotting the above data of XE(t) vs. t.
![]()
Summary
t = 30s XBatch = 0.78
t = 20s XPFR = 0.71
t = 20s XCSTR = 0.53
t = 20s XSeg = 0.7
Segregation Model Software Package Solution
![]()
![]()

Fit the RTD to one or more polynomials
E (t) = a0 + a1t + a2t2 + …

